Начетвъртена хиперкубична пита

В геометрия, начетвъртената хиперкубична пита (или четвърткубична пита) е безкрайна поредица пити, основани на хиперкубичната пита. Даден е символ на Шлефли q{4,3...3,4}, представляващ правилната форма с четвъртина върхове, които са премахнати и побират симетрията на групата на Коксетер ${\tilde {D}}_{n-1}$ за n ≥ 5, и ${\tilde {D}}_{4}$ = ${\tilde {A}}_{4}$.

qδn	Име	Символ на Шлефли	Диаграма на Коксетер	Фасети			Връхна фигура
qδ4	начетвъртена кубична пита	q{4,3,4}		{3,3}	t0,1{3,3}		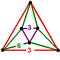удължена триъгълна антипризма
qδ5	начетвъртена тесерактична четирипита	q{4,32,4}	=	h{4,32}	t1{4,32}		осмостенна призма
qδ6	начетвъртена пентерактична петопита	q{4,33,4}		h{4,33}	t0,3(121)		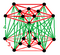осечена петоклетъчна антипризма
qδ7	начетвъртена хексерактична шестопита	q{4,34,4}		h{4,34}	t0,4(131)	{3,3}×{3,3}
qδ8	начетвъртена хептерактична седмопита	q{4,35,4}		h{4,35}	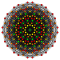t0,5(141)	{3,3}×{3,31,1}
qδ9	начетвъртена октерактична осмопита	q{4,36,4}		h{4,36}	t0,6(151)	{3,3}×{3,32,1} {3,31,1}×{3,31,1}
qδn	начетвъртена n-кубична пита	q{4,3n-3,4}	...

Вижте също

• Хиперкубична пита
• Сменена хиперкубична пита
• Симплектична пита
• Пресечена хиперкубична пита
• Всичкопресечена хиперкубична пита

Източници

• Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
• pp. 122 – 123, 1973. (The lattice of hypercubes γ_n form the cubic honeycombs, δ_n+1)
• pp. 154 – 156: Partial truncation or alternation, represented by q prefix
• p. 296, Table II: Regular honeycombs, δ_n+1
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380 – 407, MR 2,10] (1.9 Uniform space-fillings)
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3 – 45] See p318 [2]