Симетрия


Симетрията (също така съразмерност;от старогръцки: συμμετρεῖν, „измервам заедно“) е вътрешна самоподобност на даден обект, измерена чрез дадена формална система от правила. Симетричните обекти могат да бъдат материални, като кристали или молекули, или абстрактни, като уравнения или поредици от музикални тонове. В зависимост от правилата на симетрия могат да бъдат дефинирани различни видове симетрии, например:
- чрез различни геометрични трансформации, като мащабиране, отражение или ротация
- чрез други математически трансформации
- спрямо времето
- като пространствено отношение
В преносен смисъл симетрия може да означава и просто хармонична или естетически приятна пропорционалност и уравновесеност.[1] Отсъствието на симетрия се нарича асиметрия.
В геометрията[редактиране | редактиране на кода]
Най-обичайният вид симетрия е геометричната. Формално геометричните симетрии се дефинират като подгрупи на Евклидовата група изометрии в двуизмерно или триизмерно Евклидово пространство. Тези изометрии се състоят от отражения, ротации (завъртания), транслации (премествания) или съчетания от тях.
Огледална симетрия[редактиране | редактиране на кода]
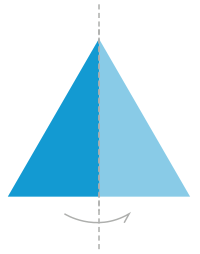 Огледалната симетрия е симетрия, дефинирана чрез трансформацията отражение. В едноизмерно пространство, например числовата ос, тя се определя спрямо точка на симетрия, в двуизмерно пространство – спрямо ос на симетрия, а в триизмерното пространство – спрямо равнина на симетрия. Обект или фигура, която е неразличима от своя огледален образ, се нарича огледално симетрична.
Огледалната симетрия е симетрия, дефинирана чрез трансформацията отражение. В едноизмерно пространство, например числовата ос, тя се определя спрямо точка на симетрия, в двуизмерно пространство – спрямо ос на симетрия, а в триизмерното пространство – спрямо равнина на симетрия. Обект или фигура, която е неразличима от своя огледален образ, се нарича огледално симетрична.
Оста на симетрия за дадена двуизмерна фигура е линия, за която на всяка точка от фигурата, лежаща от едната страна на оста, съответства точка от другата страна, разположена на същото разстояние от оста. Например квадратът има четири оси на симетрия – диагоналите и правите, дефинирани от средните точки на срещуположните страни. Кръгът има безкрайно много оси на симетрия – всеки негов диаметър представлява такава ос. Триъгълниците с огледална симетрия са равнобедрени. При четириъгълниците огледална симетрия имат делтоидите и равнобедрените трапеци.
Ротационна симетрия[редактиране | редактиране на кода]
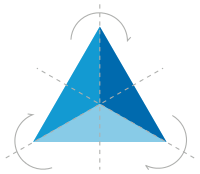 Ротационната симетрия е симетрия по отношение на някои или всички завъртания в n-мерно Евклидово пространство. Например квадратът е симетричен спрямо ротации на 90° около пресечната точка на диагоналите му, а окръжността – спрямо ротация на произволен ъгъл около нейния център.
Ротационната симетрия е симетрия по отношение на някои или всички завъртания в n-мерно Евклидово пространство. Например квадратът е симетричен спрямо ротации на 90° около пресечната точка на диагоналите му, а окръжността – спрямо ротация на произволен ъгъл около нейния център.
Ротациите са директни изометрии, т.е. такива, които запазват ориентацията, а симетричната група на ротационната симетрия е подгрупа на E+(n). Симетрията спрямо всички ротации около всички точки в пространството налага и транслационна симетрия спрямо всички транслации, като в този случай симетричната група съвпада с цялата група E+(n). Такава симетрия не е приложима към обекти, тъй като би направила пространството хомогенно, но може да се прилага към физичните закони.
За симетриите спрямо ротации около една точка тази точка може да се приеме за начало на координатната система. Такива ротации образуват специална ортогонална група SO(m), включваща всички ортогонални матрици с размер n×n и детерминанта 1. За триизмерното пространство (n=3) това е ротационната група.
Транслационна симетрия[редактиране | редактиране на кода]
 Транслационната симетрия оставя обекта неповлиян в процеса на дискретна или непрекъсната група транслации Ta(p) = p + a. Например правата е симетрична спрямо произволна транслация по нейното собствено направление. Безкрайна редица от еднакви триъгълници, разположени на равно разстояние d един от друг по права линия, е симетрична спрямо транслации на цял брой разстояния d по направление на правата.
Транслационната симетрия оставя обекта неповлиян в процеса на дискретна или непрекъсната група транслации Ta(p) = p + a. Например правата е симетрична спрямо произволна транслация по нейното собствено направление. Безкрайна редица от еднакви триъгълници, разположени на равно разстояние d един от друг по права линия, е симетрична спрямо транслации на цял брой разстояния d по направление на правата.
Роторефлекторна симетрия[редактиране | редактиране на кода]
В триизмерно пространство роторефлекция или неправилна ротация строго погледнато е ротация около ос, комбинирана с отражение в равнина, която е перпендикулярна на тази ос.
Спираловидна (хеликоидална, винтова) симетрия[редактиране | редактиране на кода]
Хеликоидалната симетрия се среща във всекидневни части като пружини, спираловидни играчки, бургии, свредели и сонди.

Може да се мисли за нея като за ротационна симетрия заедно с транслация по протежение на оста на въртене (в западните езици се нарича „винтова ос“). Идеята на хеликоидалната симетрия е графичното проследяване (трасирането) в триизмерно пространство като резултат от въртенето на обект с еднаква ъглова скорост, докато едновременно с това обекта се движи линейно по протежение на оста на въртене (т.е. обекта извършва едновременно ротация и транслация). Комбинацията от тези две движения (ротация и транслация) дава ъгъл на навивката (спираловиден, серпентинен ъгъл, ъгъл на намотката), който помага да се определят свойствата на получената графика. Например ако трасиращият обект се върти бързо, а се транслира (движи по права линия) бавно, ъгълът на намотката ще е малък, например близо до 0°. Обратно – ако ротацията е бавна, а транслацията бърза, спираловидния ъгъл ще е близко до 90°. Ако ротацията спре, а се запаси транслацията, въпросният ъгъл ще е равен на 90° (едното рамо на ъгъла е в равнина, перпендикулярна на оста на ротация, а другото е допирателната към описаната от чертаещия обект траектория).
В други области на математиката[редактиране | редактиране на кода]
В природните науки[редактиране | редактиране на кода]
Във физиката[редактиране | редактиране на кода]
Симетрията е едно от основните понятия във физиката. Тя играе важна роля във формулирането на физичните теории. Симетрията във физиката се изразява в най-различни форми, с голямо разнообразие, като се започне със симетрията в тримерното пространство и огледалната симетрия и се стигне до много по-сложни и абстрактни симетрии.
В теоретичната физика поведението на една физическа система се описва с някакви уравнения. Ако тези уравнения притежават симетрия, често решаването им се опростява чрез намиране на запазващи се величини (интеграли на движение). Така например, в класическата механика е в сила теоремата на Ньотер, която съпоставя на всеки тип непрекъсната симетрии една запазваща се величина. От нея следва например, че инвариантността на уравненията на движения на едно тяло с течение на времето води до закона за запазване на енергията; инвариантността по отношение на премествания в пространството – към закона за запазване на импулса; инвариантността по отношение на ротации – към закон за запазване на момента на импулса.
При класически обекти[редактиране | редактиране на кода]
При квантови обекти[редактиране | редактиране на кода]
Обобщения на симетрията[редактиране | редактиране на кода]
В биологията[редактиране | редактиране на кода]
Двустранно-симетричните животни (Bilateria), включително хората, са приблизително огледално симетрични спрямо сагиталната равнина.
В химията[редактиране | редактиране на кода]
В историята, религията и културата[редактиране | редактиране на кода]
Бележки[редактиране | редактиране на кода]
- ↑ Zee, Anthony. Fearful Symmetry. Princeton, 2007. ISBN 9780691134826. (на английски)
Външни препратки[редактиране | редактиране на кода]
- ((ru)) Что такое симметрия Архив на оригинала от 2013-05-02 в Wayback Machine.
- ((ru)) Симетрия във физиката

