Синусова теорема
Синусовата теорема в тригонометрията изразява пропорционалната зависимост между дължините на страните на триъгълник в равнината и синусите на ъглите срещу тях.
Ако страните на триъгълника са означени с и , а ъглите срещу тях с и , тогава синусовата теорема гласи:
За всеки триъгълник отношението на коя да е страна и синуса на срещулежащия ъгъл е равно на диаметъра на описаната около триъгълника окръжност:
- ,
където e радиусът на описаната окръжност, а е нейният диаметър (фиг. 1). Този резултат датира от Птолемей. [1][2]
Теоремата има и обикновен вариант без използване на описаната окръжност, когато последната част от уравнението не се записва (фиг. 2):
Страните на триъгълника са пропорционални на синусите на срещулежащите ъгли:
- ,
а понякога законът се изразява и с реципрочните стойности:
- .
Тези формули се използват, за да се намерят неизвестните страни на триъгълника, ако се знаят 2 ъгъла и третата страна, което е основна задача при триангулацията. Може да се използват и ако са известни две от страните и един от ъглите, но не този сключен между тях. Тогава уравненията ще дадат 2 решения за сключения ъгъл между известните страни: остър и тъп ъгъл, сумата от които е 180°, тъй като за всеки ъгъл важи равенството .
По синусовата теорема може да се определи и радиусът на описаната окръжност около триъгълника, ако се знаят една от страните му и ъгълът срещу нея:
- .
При остроъгълен и тъпоъгълен триъгълник диаметърът на описаната окръжност е по-голям от всяка от страните му, а при правоъгълен триъгълник е равен на хипотенузата.
Диаметърът на описаната окръжност може да се определи и чрез Хероновата формула за лице на триъгълника (фиг. 3):

- или
- ,
където е полупериметърът на триъгълника.
Доказателство[редактиране | редактиране на кода]
Нека е даден триъгълник със страни и и срещулежащи ъгли и (фиг. 4). От върха се спуска перпендикуляр към страната и се обозначава с . Така се получават 2 правоъгълни триъгълника. За тях са верни равенствата:
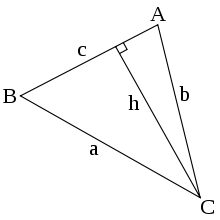
- и .
Следователно
и
- .
Същото се получава и ако се спусне перпендикуляр от върха към страната
и от върха към страната
- .
От свързването на последните три равенства се формулира синусовата теорема.
Сферична синусова теорема[редактиране | редактиране на кода]
Сферичната синусова теорема има същата формулировка и се отнася за сферичен триъгълник.
Вижте също[редактиране | редактиране на кода]
- Триъгълник
- Тригонометрична функция
- Триангулация
- Косинусова теорема
- Тангенсова теорема
- Котангенсова теорема
Източници[редактиране | редактиране на кода]
- ↑ Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 1–3, 1967
- ↑ Law of Sines // Посетен на 2018-09-18.





























