Хипотеза на Риман
За информацията в тази статия или раздел не са посочени източници. Въпросната информация може да е непълна, неточна или изцяло невярна. Имайте предвид, че това може да стане причина за изтриването на цялата статия или раздел. |
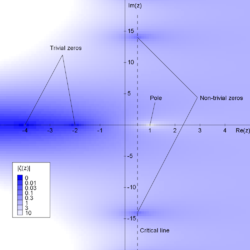
Хипотезата на Риман е известна нерешена задача от алгебричната теория на числата, свързана със свойствата на Римановата ζ-функция и разпределението на простите числа. Хипотезата гласи:
„Реалната част на всяка кратна нула на Римановата дзета-функция е равна на ½“.
Хилберт включва задачата за доказването на Римановата хипотеза в своето изложение за предизвикателствата пред математиката през ХХ век, в което той включва 23 нерешени задачи.
Римановата хипотеза и разпределението на простите числа[редактиране | редактиране на кода]
Трудно е да се види важността на Римановата хипотеза в нейната класическа формулировка. През 1901 Хелге фон Коф доказва еквивалетността на Римановата хипотеза и хипотезата, че за всяко ε>0 е вярно твърдението:
където функцията π(x) дава броя прости числа, по-малки от x, ln(x) е натуралният логаритъм, а O е функция, която „расте като“ . Лоуел Шьонфелд намира трета еквивалентна формулировка на хипотезата:
Простите нули на ζ-функцията могат да бъдат разглеждани образи на простите числа в пространството на Фурие, т.е. кратните нули на ζ-функцията могат да бъдат разглеждани като хармонични честоти на функцията, даваща разпределението на простите числа.



