Теорема на Менелай

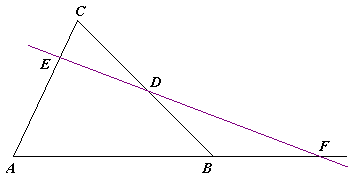
Ако през продължението на страната AB минава права, пресичаща AC, BC и продължението на AB съответно в точки E, D и F, то тогава

${\frac {AF}{FB}}\times {\frac {BD}{DC}}\times {\frac {CE}{EA}}=1.$

Доказателство: ${\frac {AF}{FB}}={\frac {S_{AFD}}{S_{BFD}}};{\frac {BD}{CD}}={\frac {S_{BDE}}{S_{DCE}}};{\frac {CE}{EA}}={\frac {S_{DCE}}{S_{EAD}}}$

Умножаваме левите и десните страни на равенствата и за дясната страна на равенството получаваме: ${\frac {AF}{FB}}\times {\frac {BD}{DC}}\times {\frac {CE}{EA}}={\frac {S_{AFD}}{S_{BFD}}}\times {\frac {S_{BDE}}{S_{EAD}}}={\frac {S_{AFD}}{S_{EAD}}}\times {\frac {S_{BDE}}{S_{BFD}}}={\frac {FD}{ED}}\times {\frac {ED}{DF}}=1.$

Тази статия, свързана с математика, все още е мъниче. Помогнете на Уикипедия, като я редактирате и разширите.