Формула на Ойлер: Разлика между версии
svg |
м без интервал; козметични промени |
||
| Ред 1: | Ред 1: | ||
[[ |
[[Файл:Euler's formula.svg|мини|360px|Графика, показваща взаимовръзката между, <math>\sin \varphi</math>, <math>\cos \varphi</math> и комплексната експоненциална функция.]] |
||
'''Формулата на Ойлер''' е математическа формула от областта на [[комплексен анализ|комплексния анализ]], показваща дълбоката връзка между [[тригонометрични функции|тригонометричните функции]] и комплексната експоненциална функция. |
'''Формулата на Ойлер''' е математическа формула от областта на [[комплексен анализ|комплексния анализ]], показваща дълбоката връзка между [[тригонометрични функции|тригонометричните функции]] и комплексната експоненциална функция. |
||
Формулата на [[Ойлер]] гласи, че за всяко реално число <math>\varphi</math>: |
Формулата на [[Ойлер]] гласи, че за всяко реално число <math>\varphi</math>: |
||
:<math>e^{i\varphi} = \cos \varphi + i\sin \varphi \!</math> |
:<math>e^{i\varphi} = \cos \varphi + i\sin \varphi \!</math> |
||
:където: е |
:където: е — основа на натуралния логаритъм, |
||
:: i |
:: i — имагинерна единица, |
||
:: <math>\sin</math> и <math>\cos</math> са [[тригонометрични функции]]. |
:: <math>\sin</math> и <math>\cos</math> са [[тригонометрични функции]]. |
||
| Ред 12: | Ред 12: | ||
Ако искаме да обясним формулата на Ойлер с най-прости думи, това е равносилно на ротация на единичен вектор на ъгъл <math>\varphi</math>. |
Ако искаме да обясним формулата на Ойлер с най-прости думи, това е равносилно на ротация на единичен вектор на ъгъл <math>\varphi</math>. |
||
==Извод== |
== Извод == |
||
Уравнението на Ойлер може да бъде изведено по много начини. Един от най-елегантните изводи прибягва до помощта на комплексен интеграл.<ref>{{cite web |
Уравнението на Ойлер може да бъде изведено по много начини. Един от най-елегантните изводи прибягва до помощта на комплексен интеграл.<ref>{{cite web |
||
| Ред 41: | Ред 41: | ||
:<math> e^{i\varphi} = \cos \varphi + i\sin \varphi \!</math>. |
:<math> e^{i\varphi} = \cos \varphi + i\sin \varphi \!</math>. |
||
===Тъждество на Ойлер=== |
=== Тъждество на Ойлер === |
||
В частния случай, когато |
В частния случай, когато |
||
| Ред 63: | Ред 63: | ||
: <math>e^{i \pi} = -1,\,\!</math> |
: <math>e^{i \pi} = -1,\,\!</math> |
||
а оттук |
а оттук |
||
: <math>e^{i \pi} +1 = 0,\,\!</math> |
: <math>e^{i \pi} +1 = 0,\,\!</math> |
||
Версия от 14:52, 5 януари 2020
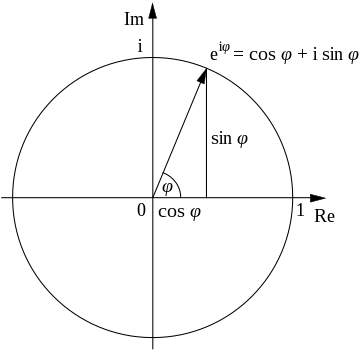
Формулата на Ойлер е математическа формула от областта на комплексния анализ, показваща дълбоката връзка между тригонометричните функции и комплексната експоненциална функция.
Формулата на Ойлер гласи, че за всяко реално число :
- където: е — основа на натуралния логаритъм,
- i — имагинерна единица,
- и са тригонометрични функции.
Ричард Файнман нарича формулата на Ойлер "скъпоценен камък" и "най-важната формула" в цялата математика (Feynman, p. 22-10).
Ако искаме да обясним формулата на Ойлер с най-прости думи, това е равносилно на ротация на единичен вектор на ъгъл .
Извод
Уравнението на Ойлер може да бъде изведено по много начини. Един от най-елегантните изводи прибягва до помощта на комплексен интеграл.[1]: Нека z е комплексно число с модул единица в тригонометричен вид
- .
След диференциране и преобразуване, получаваме
където А е произволна константа, която се определя със следното съображение:
и оттук
- .
Тъждество на Ойлер
В частния случай, когато
получаваме
Доколкото
и
следва
а оттук
Източници
- ↑ Eric W. Weisstein. Euler Formula // MathWorld. Посетен на 12 декември 2010.























