Аксиома за успоредните прави
За информацията в тази статия или раздел не са посочени източници. Въпросната информация може да е непълна, неточна или изцяло невярна. Имайте предвид, че това може да стане причина за изтриването на цялата статия или раздел. |
Аксиомата за успоредните прави за първи път е формулирана явно от Евклид в неговите „Елементи“ като постулат за успоредните прави (известен като V постулат на Евклид). Съвременната формулировка е:
За всяка права g и всяка точка S, нележаща на нея, съществува точно една права h през S, която лежи в еднозначно определената от g и S равнина и е успоредна на правата g, т.е. която не сече g.
Евклид е формулирал своя постулат така:
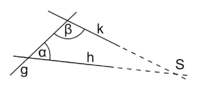
Когато една права при пресичане с две други прави образува вътрешни ъгли от една и съща нейна страна, които заедно са по-малко от два прави ъгъла, то двете прави при продължаване до безкрайност трябва да се пресекат от страната, където лежат ъглите, които заедно са по-малко от два прави ъгъла.
Твърдения, еквивалентни на аксиомата за успоредните прави[редактиране | редактиране на кода]
Още в древността е дискутиран въпросът, дали аксиомата за успоредните прави може да се докаже с другите аксиоми на Евклид. Той остава нерешен около две хиляди години въпреки многобройните опити на учените в това отношение. Те успяват само да намерят редица твърдения, еквивалентни на аксиомата за успоредните прави, но никое от тях не е доказано, без тя да бъде използвана.
Ще посочим някои от тези еквивалентни твърдения:
- Множеството от всички точки от една равнина, които се намират на равни разстояния от една и съща страна на една права, също образува права – Посидоний (ок. 135 – 51 г. пр.н.е.).
- Разстоянието между две прави, перпендикулярни на една права, е ограничено.
- През точка от вътрешността на ъгъл, по-малък от изправен, винаги може да се прекара права, която да пресича и двете рамене на ъгъла – Льожандър.
- Две неограничено приближаващи се прави се пресичат.
- За всеки триъгълник съществува подобен с произволна големина – Уолис.
- Съществува правоъгълник.
- Сборът от ъглите в триъгълника е равен на два прави ъгъла – Сакери.
- През три точки, нележащи на една права, може да се прекара окръжност.
- През точка, нележаща на дадена права, не може да минава повече от една права, успоредна на дадената.
Част от опитите да се докаже аксиомата за успоредните прави изхождат от допускане на противното, че аксиомата не е вярна. Резултат от тези изследвания са редица теореми и твърдения, които принадлежат на неевклидовата геометрия.
Неевклидови геометрии[редактиране | редактиране на кода]
До убеждението, че аксиомата за успоредните прави не може да се докаже като следствие от останалите аксиоми на Евклид, нито може да се опровергае чрез тях, а е независима от тях, първи стига Карл Фридрих Гаус, а независимо от него и помежду си Янош Бояй и Николай Иванович Лобачевски. И тримата развиват неевклидова (хиперболична) геометрия, наричана още геометрия на Лобачевски, на когото принадлежи първата ѝ публикация. Гаус не публикува откритието си, а Бояй и Лобачевски срещат пълното неразбиране на съвременните си математици. Правото на съществуване на неевклидовите геометрии е завоювано от Феликс Клайн, който построява модел на неевклидова геометрия в рамките на евклидовата геометрия.
