Неевклидова геометрия
За информацията в тази статия или раздел не са посочени източници. Въпросната информация може да е непълна, неточна или изцяло невярна. Имайте предвид, че това може да стане причина за изтриването на цялата статия или раздел. |
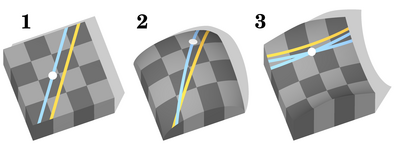
Неевклидова геометрия е термин, обединяващ хиперболичната и елиптичната геометрия, които се разграничават от евклидовата геометрия. Основната разлика между евклидовата и неевклидовата геометрия е естеството на успоредните прави. В евклидовата геометрия, ако са дадени права l и точка A, нележаща на l, то през A може да се прекара само една права, успоредна на l. В хиперболичната геометрия съществуват безброй много прави през A, успоредни на l, а в елиптичната геометрия не съществуват паралелни прави.
Друг начин да се опишат разликите между тези геометрии е следният: Нека са дадени две прави в една двумерна повърхност, които са перпендикулярни на трета права. В евклидовата и хиперболичната геометрия тези две прави са успоредни. В евклидовата геометрия обаче тези две прави остават на еднакво разстояние една от друга, докато в хиперболичната геометрия те се отдалечават една от друга, увеличавайки разстоянието помежду си с отдалечаването от точката на пресичане с общия перпендикуляр. В елиптичната геометрия линиите се приближават една към друга и накрая се пресичат – следователно в елиптичната геометрия не съществуват успоредни линии.
История[редактиране | редактиране на кода]
Докато евклидовата геометрия (наречена на гръцкия математик Евклид) включва едни от най-старите познати математически възгледи, неевклидовите геометрии не са били широко признати до 19 век. Дебатът, който накрая довежда до откриването на неевклидовите геометрии, започва с написването на евклидовите „Елементи“. В „Елементите“ Евклид започва с ограничен брой допускания (пет аксиоми и пет постулата) и се стреми да докаже всички останали резултати (теореми) в труда. Най-известният от постулатите често е наричан „пети постулат на Евклид“ или просто „постулат за успоредността“ и в оригиналната си формулировка гласи:
- „Ако една права линия пада върху две прави линии така, че вътрешните ъгли от едната страна са заедно по-малки от два прави ъгъла, то правите линии, ако се продължат безкрайно, се срещат от страната, от която ъглите са по-малки от два прави ъгъла.“
Други математици са измислили по-прости форми на това свойство (вж. „постулат за успоредността“ за еквивалентни съждения). Независимо от формата на постулата обаче той винаги се оказва по-сложен от останалите постулати на Евклид (като например „Между две точки може да се прекара права линия“).
В продължение на няколкостотин години геометрите се затрудняват от сложността на петия постулат и мислят, че той може да се докаже като теорема от останалите четири. Много от тях се опитват да намерят доказателство чрез допускане на противното, особено италианецът Джовани Сакери. В труд със заглавие „Euclides ab Omni Naevo Vindicatus“ („Евклид, освободен от всички недостатъци“), публикуван през 1733 г., той бързо отхвърля елиптичната геометрия като възможност (някои други от евклидовите аксиоми трябва да бъдат променени, за да може елиптичната геометрия да работи) и се захваща с доказване на голям брой резултати от хиперболичната геометрия. Накрая той стига до момент, в който смята, че резултатите му са показали невъзможността на хиперболичната геометрия. Неговото твърдение изглежда основано на евклидовите предположения, защото няма логическо противоречие. В опита си да докаже евклидовата геометрия всъщност, без да иска, той създава нова приложима геометрия. По това време широко е разпространено убеждението, че Вселената работи по принципите на евклидовата геометрия.
Сто години по-късно, през 1829 г., в руснакът Николай Лобачевски публикува монография за хиперболичната геометрия. По тази причина хиперболичната геометрия се нарича още „геометрия на Лобачевски“. Горе-долу по същото време унгарецът Янош Бояй също написва трактат по хиперболична геометрия, който е публикуван през 1832 г. като приложение към работа на баща му. Великият математик Карл Фридрих Гаус прочита приложението и разкрива на Бояй, че е получил същите резултати преди него, но не ги е публикувал поради страх от неразбиране.
Името на Лобачевски е дадено според правото на най-ранната публикация. Фундаменталната разлика между неговата и по-ранните работи като тази на Сакери е, че те са първите, които непредубедено заявяват, че евклидовата геометрия не е нито единствената геометрия, нито единствената възможна геометрична структура за Вселената. Лобачевски нарича евклидовата геометрия „обикновена геометрия“, а новата хиперболична геометрия – „имагинерна геометрия“. Но все пак е оставала възможността аксиомите на хиперболичната геометрия да излязат логически противоречиви.

Евклидовата геометрия се моделира от понятието „равнина“. Най-простият модел на елиптичната геометрия е сфера, където правите са големи окръжности (като екватора или меридианите на един глобус), а срещуположните точки се идентифицират (смятат се за съвпадащи). Дори след трудовете на Лобачевски, Гаус и Бояй остава въпросът, дали съществува такъв модел за хиперболичната геометрия. Отговорът е намерен от Еудженио Белтрами през 1868 г., който доказва, че повърхнина, наречена псевдосфера, има кривина, подходяща за моделиране на хиперболичната геометрия. Работата му е пряко основана на тази на Риман. Значението на труда на Белтрами е в показването, че хиперболичната геометрия е логически непротиворечива, ако евклидовата геометрия е такава.
Развитието на неевклидови геометрии се оказва много важно за физиката през 20 век. При ограничението на скоростта на светлината сумирането на скорости изисква използването на хиперболична геометрия. Айнщайновата теория на относителността описва пространството като, общо взето, равно (т.е. евклидово), но изкривено елиптично (т.е. неевклидово) в области около места, където има наличие на материя. Тъй като Вселената се разширява (виж константа на Хъбъл), пространството, където няма материя, може да се опише чрез хиперболичен модел. Този вид геометрия, в която кривината се променя в различните точки, се нарича риманова геометрия.
Има и други математически модели на равнината, в които постулатът за успоредността не е валиден, например в равнината на Ден, състояща се от всички точки (x, y), където x и y са крайни сюрреални числа.
