Хеш таблица
Тази статия съдържа списък с ползвана литература, препоръчана литература или външни препратки, но източниците ѝ остават неясни, защото липсва конкретно посочване на източници за отделните твърдения. |
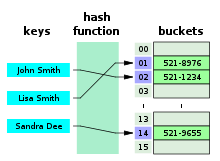
Хеш таблицата е структура от данни, съдържаща ключ и данни, която се характеризира с директен достъп до елементите, независимо от типа им. Елементите ѝ, подобно тези на други структури от данни използвани за търсене, се състоят от ключ и данни. Ключът е уникален за разлика от данните – не може да съществуват два елемента с един и същи ключ. Сложността на елементарните операции по ключ (търсене, вмъкване, изтриване и актуализиране) в общия случай е константна, което я прави изключително полезна.
Приложение
[редактиране | редактиране на кода]При процеса на компилиране на дадена програма всеки идентификатор в нея се съхранява в определена структура (таблица), в която за него има полета и за друга информация – тип, адрес от паметта и други. Когато се срещне такъв идентификатор трябва да се определи дали той вече не е сред множеството идентификатори, които вече са в таблицата. Последователното обхождане и поддържането в сортиран вид на тези структури са бавни операции. Най-удачна реализация на операциите търсене, четене и вмъкване в такова множество от идентификатори (ключове) е хеширането (от англ. „hash, hashing“). Хеширането е много добър пример за компромисно решение на проблема памет-време. При хеширането ключът се преобразува чрез определена хеш функция в адрес на таблица (хеш таблица) т.е. на дадени данни се съпоставят други, посредством правила, но така че обратната операция да е невъзможна (ако хеширате даден низ, с хеш функция, то от резултата няма как да получите обратно първоначалния низ).
Операции
[редактиране | редактиране на кода]Основните операции за работа с хеш таблица са следните три:
- Void put (key, data); – включване на елемент с ключ (key) и данни (data) в хеш таблицата
- Data get (key); – търсене и извличане на данните от елемент с ключ (key) от хеш таблицата
- Void remove (key); – изключване на елемент с ключ (key) от хеш таблицата
Всеки елемент на хеш таблицата се характеризира с две полета: ключ (key) и данни (data). Ключът представлява уникален идентификатор: ако два елемента имат един и същ ключ се считат идентични.
Хеш функции
[редактиране | редактиране на кода]Хеш функция или хеш алгоритъм е метод, който преобразува данни в число, подходящо за манипулиране от компютъра. Тези функции осигуряват начин за създаване на малки дигитални „отпечатъци“ от всякакъв тип данни. Тези „отпечатъци“ често са наричани хеш стойности. Означава се с: h (k), където k е ключ.
Фундаментално свойство на всички хешфункции е, че ако две хеш стойности (спрямо една хеш функция) са различни, то и въведените данни се различават по някакъв начин. Tова свойство е следствие от определеността на хеш функциите. От друга страна, ако две хеш стойности са еднакви, това не означава, че въведените данни са еднакви.
Изискванията при избор на подходяща хеш функция са:
- Да се изчислява бързо, лесно и с малък брой операции;
- Изчислените с нея хеш адреси да са такива, че да има минимум колизии.
Конкретната хеш функция зависи от вида на ключовете (данните). Когато те са цяло число, тя има вида:
(1) h (k) = k mod n, (остатък от делението на k с n, n – размер на таблицата.)
По този начин хеш адресът винаги е в границите на индексите на таблицата.
Когато ключът не е цяло число, а е низ, хеш функцията има вида:
(2) h (k) = f(k) mod n, f(k) – преобразува ключа в цяло число.
Тогава, когато h (k1) = h (k2) настъпва колизия. Идеална хеш функция (без колизии) няма или поне няма обосновано твърдение (с ясно математическо доказателство), че някоя хеш функция не подлежи на колизия.
Два блока с информация са в колизия, ако те се различават по съдържание, но имат един и същи хеш. Не е задължително блоковете да са два – може да са и повече (повече колизии). Една хеш функция е под заплаха, ако се намери начин за контролирано намиране на колизия (т.е. да се намери алгоритъм, който е повторим и по зададен изходен блок от информация и неговия хеш, той да позволява да се изчисли друг блок информация, който има същия хеш). За една хеш функция се казва че е разбита, ако е намерен алгоритъм за редукция на броя търсения. Колизиите се разрешават чрез отворено и затворено хеширане.
Отворено хеширане – При него таблицата е масив от указатели, които сочат динамично свързани списъци от ключове, с еднакъв хеш адрес.
Затворено хеширане – При затвореното хеширане се използва само едномерен масив и индекс:
h (k) = [h(k) + f(i)] % n, където: h(k) – оригинална хеш функция; i – пореден номер на опита (индексиране); f (i) – функция за разрешаване на колизии, като винаги f (0) = 0.
Класически хеш функции
[редактиране | редактиране на кода]Удачният избор на хеш функция се определя от две неща:
- Хеш функцията да не отнема много изчислително време.
- Да разпределя елементите относително равномерно в различните хеш адреси.
Най-често срещаните в практиката хеш функции (върху целочислен ключ):
- Остатък при деление с размера на таблицата
Ключът k се разделя целочислено на n и се взема остатъкът от делението. При този подход не е удачно за капацитет на хеш таблицата да се избира число n, степен на 2. Ако n=2p, то хеш кодът на даден ключ k ще бъдат младшите p бита на k. Например n=24, k=173.
173=10101101(2) 173 % 16=13=1101(2)
Това хеширане ще се държи лошо, ако разпределението на ключовете е такова, че има има голям брой числа със съвпадащи младши битове. Препоръчва се за капацитет на хеш таблицата да се избира просто число.
- Мултипликативно хеширане
При мултипликативното хеширане избираме реална константа a между 0 и 1 и образуваме функцията:
hash(key) = trunc(n * ((key * a) – trunc(key * a)))
Т.е. взимаме дробната част от умножението на ключа с константата и я умножаваме по размера на таблицата. Често за стойност на константата се избира
а = (sqrt (5) – 1) / 2,
т.нар. златно сечение.
Хеш функции върху части от ключа
[редактиране | редактиране на кода]При този вид хеш функции се обработва само част от ключа – използват се само цифрите стоящи на определени позиции. Такива функции обикновено се използват, когато ключът може да е много голямо число. Често се използва т.нар. сгъване – разделяне ключа на части и прилагане някаква аритметична операция върху тях.
При тази схема от ключа се извличат само цифри, намиращи се на определени позиции (например първа, трета и пета цифра от числото). Така за ключовете 123569, 425435, 676576 се получава хеш адреси съответно 136, 453, 667. Очевидно в този случай n трябва да бъде 1000. Този метод има добра успеваемост, когато числата не съдържат много повтарящи се цифри.
- Сгъване
Този метод се прилага най-често, когато ключовете са много големи числа. Методът се основава на разделяне на ключа на части и извършване на някакви аритметични действия върху получените числа (например сумата от частите да определи хеш адреса.
- Повдигане на средата в квадрат
При тази схема средните p цифри на ключа се повдигат в квадрат. Например за ключа 1256557134280980 средните три цифри са 134. 1342=17956. Ако резултатът надхвърли n се премахват първите няколко значещи цифри. Ако n=10001, то от 17956 се премахва първата цифра и полученият хеш адрес е 7956.
Хеш функции върху низове
[редактиране | редактиране на кода]Низовете са едни от най-използваните ключове при хеширането. Общата схема, по която работят хеш функциите върху тях е:
hash(key)
{
резултат = начална стойност
за всеки символ c от key
резултат = комбиниране (резултат, c)
резултат = модифициране (резултат)
резултат = допълнително_модифициране (резултат)
}
Най-простата функция за хеширане на низове е т.нар. адитивно хеширане. При него се взема остатъкът от делението на сумата от ASCII кодовете на символите, участващи в низа с размера на таблицата. Проблем при това хеширане е, че редът, в който са символите, не е от значение, което означава, че пермутациите на един низ ще имат еднакви хеш кодове. Това може лесно да се избегне например като умножим кода на символа по позицията му или на всяка стъпка удвояваме резултата преди да го комбинираме със символа.
Справяне с колизии
[редактиране | редактиране на кода]В литературата чисто терминологично са налице два вида разделение: хеширането бива отворено и затворено, а адресирането отворено и със списъци на препълванията (chaining). Това може да доведе до объркване, тъй като на отвореното адресиране съответства затвореното хеширане, а списъците с препълвания принадлежат към отвореното хеширане.
Определение: Колизия наричаме ситуация, при която два различни ключа връщат едно и също число за хеш код.
Колизиите са на практика неизбежни, когато хешираме произволно подмножество от голям набор от възможни ключове. Ето защо повечето имплементации на хеш таблици имат някаква стратегия за справяне с такива събития. Някои често срещани стратегии са описани по-долу. Всички тези методи изискват ключовете (или препратки към тях), да се съхраняват в таблицата заедно със свързаните с тях стойности.
Нареждане в списък(chaining)
[редактиране | редактиране на кода]
Най-разпространеният начин за решаване на проблема с колизиите е нареждането в списък (chaining). Той се състои в това двойките ключ и стойност, които имат еднакъв хеш код за ключа, да се нареждат в списък един след друг.
Отворена адресация (open addressing)
[редактиране | редактиране на кода]
Тази стратегия е алтернативна на нареждането в списък. Тук идеята е, че в случай на колизия се опитва да се сложи новата двойка на някоя свободна позиция от таблицата. Методите се различават по това как се избира къде да се търси свободно място за новата двойка. Освен това трябва да е възможно намирането на тази двойка на новото ѝ място. Този тип методи са неефективни при голяма степен на запълненост.
Линейно пробване (linear probing)
[редактиране | редактиране на кода]Използването на линейно пробване като метод за решаване на проблема с колизиите е неефективно и трябва да се избягва.
Този метод е един от най-лесните за имплементация. Представлява следният простичък код:
int newPosition = (oldPosition + i) % capacity;
където capacity е капацитетът на таблицата, oldPosition е позицията на която получаваме колизия, а i е номер на поредното пробване. Ако новополучената позиция е свободна, то мястото се използва, ако не пробваме отново като увеличаваме i с единица. Пробването може да е напред, както сме показали тук, или назад. Пробването назад става като вместо да прибавяме, вадим i от мястото, където е възникнала колизия.
Предимството при този метод е сравнително бързото намиране на нова позиция. Тъй като има висока вероятност, ако на едно място е имало колизия, в бъдеще да има и още, методът е силно неефективен.
Квадратично пробване (Quadratic probing)
[редактиране | редактиране на кода]Това е класически метод. Той се различава от линейното пробване по това, че използва квадратна функция на i (номер на поредното пробване) за намиране на следваща позиция (C#):
int newPosition = (oldPosition + c1*i + c2*i*i) % capacity;
Тук се появяват две константи c1 и c2, като се иска c2 да е различна от нула. В противен случай се връщаме на линейно пробване.
От избора на константите зависи кои позиции ще пробваме. Например, ако изберем да са равни на 1, ще пробваме последователно oldPosition, oldPosition + 2, oldPosition + 6 и т.н. За таблица с капацитет от вида 2n е най-подходящо c1 и c2 да се изберат равни на 0,5.
Двойно хеширане (double hashing)
[редактиране | редактиране на кода]При този метод се прави повторно хеширане на вече намерения хеш код, но с друга хеш функция, съвсем различна от първата. Този метод е по-ефективен от линейното и квадратичното пробване, тъй като всяко следващо пробване зависи от стойността на ключа, а не от позицията определена за ключа в таблицата. Това има смисъл, защото позицията за даден ключ зависи от текущия капацитет на таблицата.
Квадратичното пробване е по-ефективно от линейното.
Хеширане в Java
[редактиране | редактиране на кода]- метод hashCode на класа Object: public int hashCode()
- ограничаване до конкретен размер на масив – например: h(k) = abs(k.hashCode())%N
- хеш кодове за примитивни стойности:
- – за стойности от числов тип с размер по-малък или равен на int: самата стойност или битовата последователност (при float) интерпретирана като стойност от тип int.
- – за стойности от тип с размер (2 пъти) по-голям от int (long, double) – изключващо или на 2-те половини, интерпретирани като стойност от тип int.
- хеш кодове за ключове, комбиниращи множество примитивни стойности или обекти: събиране с умножение на междинните суми по просто число (31). Например за масив от символи а :
int h = 0;
for(int i = 0; i < a.length; i++)
{
h = 31 * h + a[i];
}
За масив от обекти a:
int h = 0;
for(int i = 0; i < a.length; i++)
{
h = 31 * h + (a[i] != null ? a[i].hashCode() : 0);
}
Реализация
[редактиране | редактиране на кода]По-долу е дадена примерна реализация на основните операции върху хеш таблица с отворено хеширане (списък на препълванията) на C++. Използват се наготово функции за работа със списъци, за да не се утежнява кода с тяхната реализация.
void OpenHashTable::Put(HashTable::KeyType key, HashTable::DataType data)
{
HashedKeyType i = HashFunction(key);
list *l = listFind(mOpenTable[i], key);
if (l)
{
l->data = data;
}
else
{
if (mOpenTable[i])
++mCollisionsCount;
listInsert(&mOpenTable[i], key, data);
}
}
HashTable::DataType OpenHashTable::Get(HashTable::KeyType key)
{
HashedKeyType i = HashFunction(key);
list *l = listFind(mOpenTable[i], key);
return l ? l->data : NOT_FOUND;
}
void OpenHashTable::Remove(HashTable::KeyType key)
{
HashedKeyType i = HashFunction(key);
if (mOpenTable[i]) listDelete(&mOpenTable[i], key); }
Вижте също
[редактиране | редактиране на кода]Външни препратки
[редактиране | редактиране на кода]- Какво е хеш таблица в softuni.bg
- Hash Table
- YouTube-hash
- Hash
- Creating A HashTable
- Java HashMap example Архив на оригинала от 2014-03-30 в Wayback Machine.
Литература
[редактиране | редактиране на кода]- Наков, С. Въведение в програмирането със C#. В. Търново, Фабер, 2011. ISBN 978-954-400-527-6.
- Charles E. Leiserson, The Common Lisp Cookbook Project, MIT-Scheme, Panu Kalliokoski, Department of Computer Science, University of Regina
