Котангенс

Котангенсът е тригонометрична функция, дефинирана като:

ctgx={\frac {\,\cos x}{\,\sin x}}

за всяко реално x ≠ k.π, където к е цяло число. Тази точка се изключва от дефиниционната област на котангенса, понеже той е дефиниран като частно и знаменателят не може да бъде равен на нула. Бележи се с ctg, cotg или cot.

Дефиниция

За остър ъгъл в правоъгълен триъгълник котангенсът се дефинира като отношението на прилежащия катет към срещулежащия. За обобщен ъгъл с радианна мярка x ≠ k π, чийто връх е в координатното начало, а първото рамо е по абсцисната ос, ctg x е абсцисата на точката, в която второто рамо на ъгъла пресича оста на котангенсите – допирателната към единичната окръжност, прекарана през точката с координати (0,1).

Формули и свойства

Някои от свойствата на функцията котангенс са:

Функцията котангенс е нечетна функция, понеже ctg (-x) = – ctg x.
Функцията котангенс е периодична функция с период π, понеже ctg x = ctg (x + kπ).
Функцията котангенс не е ограничена функция, тъй като tg 0 = ∞, tg π = -∞.
За функцията котангенс са изпълнени:

ctg x = 1/ tg x,

1 + ctg² x = 1/sin²x,

Котангенс на сбор и разлика на два ъгъла

ctg (x + y) = (ctg x . ctg y -1) / (ctg y + ctg x),

ctg (x – y) = (ctg x . ctg y + 1) / (ctg y – ctg x).

Котангенс на удвоен ъгъл

ctg 2x = (ctg² x-1) / 2 ctg x.

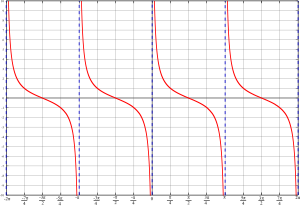
Графика на функцията

Графиката на котангенса е показана на следващия чертеж. Като вземем предвид равенството

ctg x = tg (π/2 – x),

виждаме, че графиката на котангенса може да се получи от графиката на тангенса посредством една симетрия и една транслация.

Вижте също