Тригонометрична функция
Тригонометричните функции в математиката са функции на ъгли. Използват се в геометрията за изследване на триъгълници и моделиране на периодични процеси. Най-често тригонометричните функции се дефинират като:
- отношение на две страни на правоъгълен триъгълник;
- координати на точка от единичната окръжност (окръжност с радиус 1 и център – началото на координатната система).
В най-общ вид в съвременната математика тригонометричните функции се дефинират като
- решения на някои диференциални уравнения;
- безкрайни числови редове, което позволява да се додефинират и за комплексен аргумент или да приемат произволна положителна или отрицателна стойност.

Тригонометрични функции в правоъгълен триъгълник
[редактиране | редактиране на кода]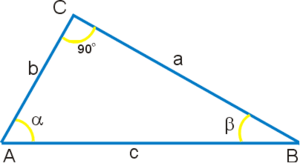
Разглежда се правоъгълен триъгълник в евклидовата равнина (фиг. 1), поради което сборът от вътрешните му ъгли е равен на 180° (π радиана). Следователно ° или .
Дефиниции
[редактиране | редактиране на кода]Синус на ъгъл е отношението на срещулежащия катет към хипотенузата:
- .
Това отношение не зависи от триъгълника АВС с остър ъгъл , тъй като всички правоъгълни триъгълници с остър ъгъл са подобни.
Косинус на ъгъл е отношението на прилежащия катет към хипотенузата:
- .
Тангенс на ъгъл е отношението на срещулежащия катет към прилежащия:
- .
Котангенс на ъгъл е отношението на прилежащия катет към срещулежащия:
- .
Секанс на ъгъл е отношението на хипотенузата към прилежащия катет:
- .
Косеканс на ъгъл е отношението на хипотенузата към срещулежащия катет:
- .
Тригонометричните функции, дефинирани чрез единична окръжност
[редактиране | редактиране на кода]Определянето на тригонометричните функции чрез единична окръжност е частен случай на дефинициите чрез правоъгълен триъгълник с хипотенуза, равна на единица. Нека в равнината е зададена правоъгълна координатна система с начало точка О и оси OE и OF. Разглежда се окръжност с център точка О и радиус, равен на единица. Построява се произволен радиус ОА, който сключва ъгъл с абсцисната ос OE (фиг. 2).

От правоъгълния триъгълник OCA
- ,
тъй като дължината на радиуса ОА е равна на 1. От тук следва определението:
Синус на даден ъгъл , отчетен от абсцисната ос, се нарича ординатата АC на пресечната точка А на другото му рамо с единична окръжност:
- .

По същия начин се получават определенията и за другите тригонометрични функции:
Косинус на даден ъгъл , отчетен от абсцисната ос, се нарича абсцисата OC на пресечната точка А на другото му рамо с единична окръжност:
- .
Тангенс на даден ъгъл , отчетен от абсцисната ос, се нарича отношението на ординатата на пресечната точка А на другото му рамо с единична окръжност, към нейната абсциса:
- , .
Котангенс на даден ъгъл , отчетен от абсцисната ос, е отношението на абсцисата на пресечната точка А на другото му рамо с единична окръжност, към нейната ордината:
- , .
Дефинициите на функциите „секанс“ и „косеканс“ се формулират малко по-сложно.
Секанс на даден ъгъл , отчетен от абсцисната ос, се нарича абсцисата OE на пресечната точка E на абсцисната ос и допирателната към единична окръжност в пресечната точка А на другото рамо на ъгъла с окръжността:
- , .
Косеканс на даден ъгъл , отчетен от абсцисната ос, се нарича ординатата OF на пресечната точка F на ординатната ос и допирателната към единична окръжност в пресечната точка А на другото рамо на ъгъла с окръжността:
- , .
В допълнение към шестте изброени съотношения, има допълнителни тригонометрични функции, които са били исторически важни, макар и рядко използвани днес (фиг. 3):

- versin, vers или sin vers:
- versin(θ) = 1 − cos(θ) = 2 sin2(θ2)
- (появява се в най-ранните таблици); [1]
- веркосинус или косинус версус –
- vercos или cos vers:
- vercos(θ) = 1 − sin(θ) = versin(π2 − θ) ;
- хаверсинус – haversin или hav:
- haversin(θ) = 12versin(θ) = sin2(θ2) ; [2]
- хаверкосинус – havercos или hac:
- havercos(θ) = 12vercos(θ) = cos2(θ2);
- екссеканс – exsec(θ) = sec(θ) − 1;
- екскосеканс – excsc(θ) = exsec(π2 − θ) = csc(θ) − 1.

Свойства
[редактиране | редактиране на кода]Свойства на функцията синус
[редактиране | редактиране на кода]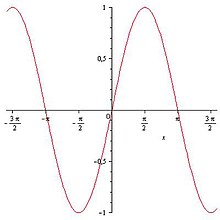
- Дефиниционна област (допустими стойности на аргумента, за които функцията е определена) – множеството на всички реални числа: .
- Множество на стойностите на функцията – областта
[−1; 1]: [−1;1]. - Функцията е нечетна: .
- Функцията е периодична, най-малкият положителен период е равен на : .
- Графиката на функцията пресича оста Ох при .
- Области с постоянен знак:
при и
при . - Функцията е непрекъсната и има производна при всяка стойност на аргумента:
- Функцията е растяща при , и намаляваща при .
- Функцията има минимум при и максимум при .
Свойства на функцията косинус
[редактиране | редактиране на кода]
- Дефиниционна област (област на определяне) – множеството на всички реални числа: .
- Множество на стойностите – областта [−1; 1]:
= [−1;1]. - Функцията е четна: .
- Функцията е периодична, най-малкият положителен период е равен на : .
- Графиката на функцията пресича оста Ох при .
- Области с постоянен знак:
при и
при . - Функцията е непрекъсната и има производна при всяка стойност на аргумента:
- Функцията е растяща при и е намаляваща при .
- Функцията има минимум при и максимум при .
Свойства на функцията тангенс
[редактиране | редактиране на кода]
- Област на определяне на функцията – множеството от всички реални числа: , освен числата .
- Множество на стойностите – множеството на всички реални числа: .
- Функцията е нечетна: .
- Функцията е периодична. Най-малкият положителен период е равен на : .
- Графиката на функцията пресича оста Ох при .
- Области с постоянен знак:
при и
при . - Функцията е непрекъсната и има производна при всяка стойност на аргумента:
- Функция расте при .
Свойства на функцията котангенс
[редактиране | редактиране на кода]
- Област на определяне на функцията – множеството на всички реални числа: освен числата
- Множество на стойностите – множеството на всички реални числа: .
- Функцията е нечетна: .
- Функцията е периодична, най-малкият положителен период е равен на : .
- Графиката на функцията пресича оста Ох при .
- Области с постоянен знак:
при и
при . - Функцията е непрекъсната и има производни при всяка стойност на аргумента:
- Функцията намалява при .
Обобщени свойства
[редактиране | редактиране на кода]Функцията косинус е четна, а синус, тангенс и котангенс – нечетни, т.е.
- , ,
- , .
За остри ъгли
- , ,
- , ,
- , ,
- , .
За ъгли е изпълнено
- , ,
- , ,
- ,
- ,
- ,
- .
Знакът на функциите sin, cos, sec и cosес се променя през интервали от 180°, а на tg и cotg – през 90°.
- за или
- für или
- за oder
- за или
- за или
- за или
- за или
- за или
- за или
- за или
- за или
- за или
Таблицата показва знаците на тригонометричните функции в зависимост от квадранта:
| Квадрант | sin и csc | cos и sec | tan и cot |
|---|---|---|---|
| I | + | + | + |
| II | + | − | − |
| III | − | − | + |
| IV | − | + | − |
В следващата таблицата са дадени най-основните свойства на тригонометричните функции.
| Функция | Озна-чения | Изразяване чрез основна връзка | Дефиниционна област | Област на стойностите |
|---|---|---|---|---|
| Синус | [–1; 1] | |||
| Косинус | [–1; 1] | |||
| Тангенс | или | без , |
||
| Котангенс | , или | без , |
Връзки между функциите
[редактиране | редактиране на кода]Тъждества се наричат равенства, изпълнени за всички допустими стойности на променливите в тях. Стандартните тъждества на връзките между функциите са
От правоъгълния триъгълник ABC (фиг. 1) съгласно теоремата на Питагор
- ,
и тъй като AB = 1, AC = sin α и BC = cos α, то
- .
В следващата таблица са дадени всички връзки между тригонометричните функции. Всяка от функциите е изразена чрез всяка от другите пет.
| sin | cos | tan | cot | sec | csc | |
|---|---|---|---|---|---|---|
| sin(x) | ||||||
| cos(x) | ||||||
| tan(x) | ||||||
| cot(x) | ||||||
| sec(x) | ||||||
| csc(x) |
При използване на формулите трябва да се имат предвид, че знакът определя две стойности.
Тригонометричните функции като редове
[редактиране | редактиране на кода]Като се използват геометрични съображения и свойствата на границите, може да се докаже, че производната на синуса е равна на косинуса на същия ъгъл и производната на косинуса е равна на производната на синуса със знак минус. Тогава с помощта на редовете на Тейлър се представят синусът и косинусът като степенни редове:
,
.
Ползвайки тези формули, а също и равенствата и може да се разложат в ред и другите тригонометрични функции:
където са числа на Бернули, са числа на Ойлер.
Косинусът като скаларно произведение
[редактиране | редактиране на кода]Във векторната геометрия косинусът се определя от скаларното произведение на два вектора u и v и техните норми ||u|| и ||v||:
- .
Пресмятане на тригонометрични функции
[редактиране | редактиране на кода]Тригонометричните функции са включени в едни от най-рано използваните математически таблици. Тези таблици са част от справочниците по математика и студентите по различни инженерни дисциплини в миналото са обучавани да ги използват при изчислителните задачи и проекти.
Днес тригонометричните функции (sin, cos, tan, cot, sec, csc) се пресмятат с калкулатори от по-високо ниво. Повечето позволяват избора на измервателната единица за ъгъл: DEG, RAD, GRAD. При съвременните компютри съществуват голям брой програми, които осигуряват изключително точни и пълни изчисления.
Стойности на тригонометрични функции за някои ъгли
[редактиране | редактиране на кода]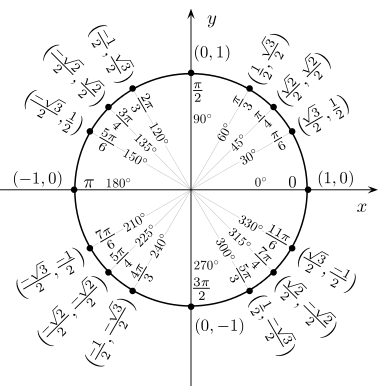
Стойностите на синус, косинус, тангенс, котангенс, секанс и косеканс за някои ъгли са дадени в таблиците. („“ означава, че функцията в указаната точка не е дефинирана, но клони към безкрайност в нейната близост).
Основни стойности
[редактиране | редактиране на кода]| Радиани | ||||||||
|---|---|---|---|---|---|---|---|---|
| Градуси | ||||||||
Стойности на тригонометрични функции за нестандартни ъгли
[редактиране | редактиране на кода]| Радиани | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Градуси | |||||||||
| Радиани | ||||||||
|---|---|---|---|---|---|---|---|---|
| Градуси | ||||||||
Литература
[редактиране | редактиране на кода]- Lars Ahlfors. Complex Analysis: an introduction to the theory of analytic functions of one complex variable, segona edició, McGraw-Hill Book Company, Nova York, 1966.
- Abramowitz, Milton; Irene A. Stegun. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Dover, Nova York. (1964). ISBN 0-486-61272-4.
- Boyer, Carl B. – A History of Mathematics, John Wiley & Sons, Inc., segona edició. (1991). ISBN 0-471-54397-7.
- Joseph, George G. The Crest of the Peacock: Non-European Roots of Mathematics, segona edició Penguin Books, Londres. (2000). ISBN 0-691-00659-8.
- Kantabutra, Vitit. "On hardware for computing exponential and trigonometric functions," IEEE Trans. Computers 45 (3), 328–339 (1996).
- Maor, Eli. Trigonometric Delights Arxivat 2006-04-14 a Wayback Machine., Princeton Univ. Press. (1998). Reimpressió (25 febrer de 2002): ISBN 0-691-09541-8.
- Needham, Tristan. "Preface" Arxivat 2004-06-02 a Wayback Machine." a Visual Complex Analysis Arxivat 2008-06-07 a Wayback Machine.. Oxford University Press, (1999). ISBN 0-19-853446-9.
- O'Connor, J.J.; E.F. Robertson. "Trigonometric functions" Arxivat 2013-01-20 a Wayback Machine., Arxiu d'història de les matemàtiques a MacTutor. (1996).
- O'Connor, J.J.; E.F. Robertson. "Madhava of Sangamagramma", Arxiu d'història de les matemàtiques a MacTutor. (2000).
- Pearce, Ian G. "Madhava of Sangamagramma" Arxivat 2006-05-05 a Wayback Machine.. Arxiu d'història de les matemàtiques a MacTutor. (2002).
- Weisstein, Eric W. "Tangent" a MathWorld, accés el 21 de gener de 2006.
Вижте също
[редактиране | редактиране на кода]- Тригонометрия
- Списък с интеграли на тригонометрични функции
- Обратни тригонометрични функции
- Аркуссинус
- ↑ Boyer 1991, с. xxiii–xxiv.
- ↑ Nielsen 1966, с. xxiii–xxiv.




























































































































































































































































































































































