Функция на разпределение на простите числа
Облик
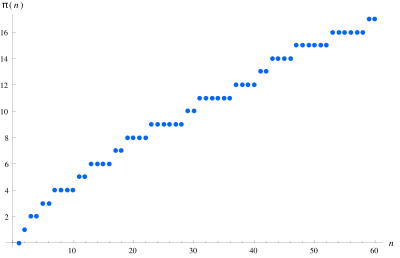
Функцията на разпределение на простите числа е математическа функция, равна на броя прости числа, по-малки или равни на реалния аргумент x.[1] Тя обикновено се обозначава с π(x) (без връзка с числото π).
Функцията на разпределение на простите числа играе важна роля в теорията на числата. Според теоремата за разпределението на простите числа π(x) може да се изчисли приблизително от
- ,
като съотношението между π(x) и тази дроб клони към 1 когато x клони към безкрайност.[2] Като следствие вероятността произволно избрано число между 1 и x да е просто, е обратнопропорционална на броя на десетичните цифри в x. Още по-добро приближение на π(x) се получава чрез интегралната функция Li(x), дефинирана като
- .
Бележки
[редактиране | редактиране на кода]- ↑ Bach, Eric. Algorithmic Number Theory. MIT Press, 1996. ISBN 0-262-02405-5. с. volume 1 page 234 section 8.8.
- ↑ Bateman 2004.
Цитирани източници
[редактиране | редактиране на кода]- Bateman, P. T. et al. Analytic number theory: an introductory course. New Jersey, World Scientific, 2004. ISBN 978-981-256-080-3. OCLC 492669517. (на английски)
Тази статия, свързана с математика, все още е мъниче. Помогнете на Уикипедия, като я редактирате и разширите.



