Хипотеза на Голдбах

Хипотезата на Голдбах (Goldbach's conjecture) е един от най-старите и най-известни неразрешени проблеми в теорията на числата, и изобщо в математиката. Тя гласи:
- Всяко четно число по-голямо от 2 може да бъде изразено като сбор от две прости числа.
Хипотезата е в сила до , но остава недоказана въпреки значителните усилия.
Числото на Голдбах[редактиране | редактиране на кода]
Числото на Голдбах е цяло положително число, което може да бъде изразено като сбор от две нечетни прости числа.
Eдинственото четно просто число е две, а четири е единственото четно число по-голямо от 2, което е сбор от две прости числа, друга формулировка на израза на хипотезата на Голдбах, е че всички четни числа по-големи от 4 са числа на Голдбах.
Изразът на дадено четно число като сбор от две прости се нарича Голдбах partition на това число. Следните са примери за числа на Голдбах за някои четни числа:
- 6 = 3 + 3
- 8 = 3 + 5
- 10 = 3 + 7 = 5 + 5
- 12 = 7 + 5
- ...
- 100 = 3 + 97 = 11 + 89 = 17 + 83 = 29 + 71 = 41 + 59 = 47 + 53
- ...
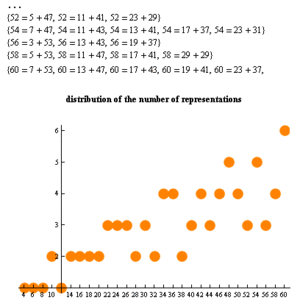
Последователността от начини, в които 2n може да бъде изписано като сбор от две прости числа (за n започващ от 1) е:
- 0, 1, 1, 1, 2, 1, 2, 2, 2, 2, 3, 3, 3, 2, 3, 2, 4, 4, 2, 3, 4, 3, 4, 5, 4, 3, 5, 3, 4, 6, 3, 5, 6, 2, 5, 6, 5, 5, 7, 4, 5, 8, 5, 4, 9, 4, 5, 7, 3, 6, 8, 5, 6, 8, 6, 7, 10, 6, 6, 12, 4, 5, 10, 3, ... Шаблон:OEIS.
Произход[редактиране | редактиране на кода]

На 7 юни 1742 г. немският математик Кристиан Голдбах написва писмо до именития си колега Леонард Ойлер(писмо XLIII)[3], в което предлага следната хипотеза:
- Всяко цяло число, което може да бъде записано като сбор от две прости числа, може също да бъде изписано като сбор от колкото прости числа пожелае човек, докато всички те не станат единици.[4]
Продължения и обобщения[редактиране | редактиране на кода]
Класическото предположение на Голдбах за четните числа понякога се определя като 'силно', докато търдението, че всяко нечетно число се представя като сума от три прости, се нарича слабо. В действителност то е следствие от силното тъй като с добаването на 3 всички нечетни числа след 5 биха се представяли в този вид т.е. 2n + 3 = p + q +3, където p и q са прости. Слабото предположение е доказано строго от Харалд Хелфгот[5] в 2013 г.
В 1894, Емил Льомоан е изказал предположение, което сега носи неговото име[6]: всяко нечетно число след 3 може да бъде представено във вида 2p + q където p и q са прости.
Източници[редактиране | редактиране на кода]
- ↑ "Goldbach's Conjecture" by Hector Zenil, Wolfram Demonstrations Project, 2007.
- ↑ Correspondance mathématique et physique de quelques célèbres géomètres du XVIIIème siècle (Band 1), St.-Pétersbourg 1843, pp. 125 – 129
- ↑ www.math.dartmouth.edu
- ↑ Голдбах е включвал 1 между простите числа
- ↑ ^ Helfgott, Harald A. (2013). "The ternary Goldbach conjecture is true". arXiv:1312.7748 (math.NT).
- ↑ Dickson, Leonard E. (1971). History of the Theory of Numbers (4 volumes). 1. S.l.: Chelsea. p. 424. ISBN 0-8284-0086-5.

