Червено-черно дърво

Червено-черно дърво
	Червено-черно дърво
Информация
Тип	tree
Година	1972
Изобретено от	Рудолф Байер
Сложност в O-нотация
	Червено-черно дърво в Общомедия

Червено-черното дърво е вид самобалансиращо двоично дърво за търсене. Всеки елемент от двоичното дърво съдържа допълнителен бит, като този бит често се интерпретира като цвят (червен или черен) на елемента. Този цветен бит се използва за да се осигури, че дървото остава относително балансирано по време на въвеждане и изтриване. Баланса се контролира, като се „оцветяват“ отделните елемнти в един от двата цвята (червено или черно) по определени критерии. Това ограничава разбалансирането на дървото, дори и в най-лошия случай. След като дървото се модифицира, настъпва последователно преподреждане и преоцветяване, за да се възстановят цветовите свойства. Тези свойства са проектирани така, че преподреждането и преоцветяването да се извършват бързо.

Балансирането на дървото не е идеално, но позволява ефективно търсене — за време O(log n), където n е броят на елементите в дървото. Операциите вмъкване и изтриване, преподреждане и преоцветяване стават също за време O(log n).

История[редактиране | редактиране на кода]

През 1972 Рудолф Байер създава структура от данни, която има специална подредба — четири случая на Б-дърво. Тези дървета поддържат всички пътища от корените до листата с еднакъв брой разклонения, създавайки идеално балансирани дървета. Въпреки това те не са двоични дървета за търсене. Байер ги нарича „симетрични двоични Б-дървета“ в записките си, но по-късно те стават известни като 2-3-4 дървета и 2–4 дървета.

В една записка от 1978 г. със заглавие „Двуцветна структура за балансирани дървета“ Леонидас Дж. Гуибас и Робърт Седжуик извличат червено-черното дърво от симетричното двоично Б-дърво. Цветът „червено“ е избран, защото по това време е бил най-добре пресъздаван от цветните принтери, достъпни за авторите, които работят в Xerox PARC. Според разказа на проф. Гуибас двамата тогава разполагали само с червени и черни химикали за рисуването на дърветата.

През 1993, Андерсън представя идеята за дясно наклонено дърво с цел опростяване въвеждащите и изтриващи операции.

През 1999, Окасаки показал как може да се направи въвеждащата операция изцяло функционална. Неговата балансираща функция трябвало да се погрижи само за 4 небалансирани случая и един дефолтен балансиран случай.

Оригиналният алгоритъм използвал 8 небалансирани случая, но Кормен ет. Ал. (2001) ги намалил до 6 небалансирани. Седжуик показъл, че въвеждащата операция може да бъде имплементирана само с 46 реда код на Java. През 2008, Седжуик предложил ляво-наклонено червено-черно дърво, противоположно на идеята на Андерсън за опростяване на алгоритми. Седжуик първоначално разрешил разклонения чийто два дъщерни елемента са червени, приличайки повече като 2-3-4 структурни дървета, но по-късно е добавено ограничение, правейки новите дървета повече като 2 – 3 дървета. Впоследствие Седжуик имплементирал въвеждащ алгоритъм само от 33 реда код, намалявайки значително оригиналните 46 реда код.

Терминология[редактиране | редактиране на кода]

Червено-черно дърво е специален тип бинарно дърво, използвано в компютърните науки за класификация на фрагменти от сравними данни, като част от текст или числа.

Листовите разклонения на червено-черните дървена не съдържат данни. Тези листа не трябва да бъдат експлицитни в компютърната памет – зададеният дъщерен елемент показва, че елемента е листо – но опростява някои от алгоритмите за операции на червено-черните дървета, ако листата наистина са експлицитни разклонения. За спестяване памет, понякога един-единствен сентинално разклонение върши ролята на всички зададени листни разклонения; всички референции от вътрешните разклонения до листните сочат към сентинелното разклонение.

Червено-черните дървета, като всички бинарно търсещи дървета, позволяват ефективно подредено търсене (което е в ред: ляво-корен-дясно) на техните елементи. Времето за намиране на резултати от търсенето от корен към листо, следователно балансирано дърво с n разклонения, имайки възможно най-малката височина на дървото, се получава О(log n) време за търсене.

Свойства[редактиране | редактиране на кода]

В допълнение на изискванията, изброени в бинарно дърво трябва да бъдат изпълнени и следните условия:

Всеки елемент има само черен или червен цвят.
Основния елемент е черен. Това правило понякога се пропуска. Понеже основния елемнт винаги може да бъде променен от черен на червен, това правило има малък ефект върху анализа.
Ако един елемнт е червен, и двете му деца са черни.
Всеки път от даден елемент до кой да е празен елемент от неговите наследници, съдържа еднакъв брой черни елемнти.

Ето някои дефиниции:

броя на черните елементи от основния до даден елемент се нарича черна дълбочина;
постоянния брой черни елементи от основата до даден изход се нарича черна височина на червено-черното дърво.^[2]

Тези ограничения налагат едно критично свойство на червено-черните дървета: пътят от основата до най-отдалеченото листо е не повече от двойния път до най-близкото . Резултата е, че дървото е грубо балансирано по височина. Понеже операции като вмъкване, изтриване и търсене изисква време, пропорционално в най-лошия случай на височината на дървото, ограничената височина позволява на дървото да бъде по-ефективно от обикновеното двоично дърво.

Аналогия с В-дървета от 4-ти ред[редактиране | редактиране на кода]

Червено-черното дърво е подобно като структура на B-дърво от 4-ти ред, където всеки възел може да съдържа между 1 и 3 стойности и (съответно) между 2 и 4 указателя към деца. В такова B-дърво, всеки възел съдържа само една стойност, съвпадаща със стойността в черен възел от червено-черно дърво, с допълнителна (незадължителна) стойност преди и/или след нея в същия възел, като и двете съвпадат с еквивалентен червен възел на червено-черно дърво.

Един от начините да се види тази еквивалентност е да „се придвижат нагоре“ червените възли в графичното представяне на червено-черно дърво, така че те да се приравнят хоризонтално с техния черен възел-родител, чрез съвместно създаване на хоризонтален клъстер. В B-дърво или в модифицираното графично представяне на червено-черно дърво, всички листни възли са на една и съща дълбочина.

След това червено-черното дърво е структурно еквивалентно на B-дърво от 4-ти ред, с минимален коефициент на запълване 33% от стойностите на клъстер, с максимален капацитет от 3 стойности.

Все пак, този вид B-дърво е все още по-общ от червено-черното дърво, тъй като позволява двусмислие при преобразуване в червено-черно дърво – множество червено-черни дървета могат да бъдат направени от еквивалентно B-дърво от 4-ти ред. Ако клъстер на B-дърво съдържа само една стойност, което е минимално, е черно, и има два указателя към деца. Ако клъстер съдържа 3 стойности, тогава централната стойност ще бъде черна и всяка стойност, съхранявана от двете страни ще бъде червена. Ако обаче клъстер съдържа две стойности, всяка една може да стане черен възел в червено-черно дърво (а другата ще бъде червена).

B-дървото от 4-ти ред не поддържа коя от стойностите, които се съдържат във всеки клъстер, е основното черно дърво за целия клъстер и родител на останалите стойности в същия клъстер. Въпреки това, операциите в червено-черните дървета са по-икономични по отношение на времето, тъй като не е нужно да се поддържа векторът на стойностите. Може да бъде времеемко, ако стойностите се съхраняват директно във всеки възел, вместо да се съхраняват чрез препратка. Възлите в B-дървото, обаче, са по-икономични по отношение на пространството, защото не е нужно да се съхраняват цветовите атрибути на всеки възел. Вместо това, трябва да знаете кой слот в клъстерния вектор е използван. Ако стойностите се съхраняват референтно, например обекти, могат да се използват нулеви референции и така клъстера може да бъде представен чрез вектор, съдържащ 3 слота за указатели към стойностите плюс 4 слота за препратки към деца в дървото. В този случай, B-дървото може да бъде по-компактно в паметта, подобрявайки местоположението на данните.

Приложения и свързани структури от данни[редактиране | редактиране на кода]

Червено-черни дървета предлагат гаранции в най-лошия случай (worst-case guarantees) за времето за вмъкване, изтриване и търсене. Това ги прави ценни не само в приложения чувствителни по отношение на времето за работа, като например приложения в реално време, но това ги прави ценни и в градивни елементи в други структури от данни, които осигуряват гаранции в най-лошия случай (worst-case guarantees); например, много структури от данни, използвани в компютърната геометрия може да са базирани на червено-черно дървета, а Completely Fair Scheduler използван в сегашните Линукс ядра използва червено-черни дървета.

AVL дървото е друга структура, която поддържа O(log n) търсене, вмъкване и изтриване. Тя е по-строго балансирана отколкото червено-черните дървета, което води до по-бавно вмъкване и изтиване, но по-бързо обработване. Това го прави привлекателен за структури от данни, които могат да бъдат изградени веднъж и зареден без реконструкция, като например езикови речници (или програмни речници, като опкодовете на един асемблер или интерпретатор).

Червено-черните дървета също са особено ценни във функционалното програмиране, където те са едни от най-често срещаните устойчиви структури от данни, използвани за изграждане на асоциативни масиви и сетове, които могат да запазят предишните версии след промени. Постоянната версия на червено-черните дървета изисква O(log n) пространство за всяко вмъкване или изтриване, в допълнение към времето.

За всяко 2 – 4 дърво има съответстващи червено-черни дървета с елементи на данните в същия ред. Операциите на вмъкване и изтриване върху 2 – 4 дървета също са еквивалентни на промяната на цвета и ротациите в червено-черните дървета. Това прави 2 – 4 дърветата важен инструмент за разбиране на логиката зад червено-черно дървета и това е причината много уводни текстове за алгоритми да представят 2 – 4 дървета точно преди червено-черните дървета, въпреки че 2 – 4 дърветата не са често използвани в практиката.

През 2008 г., Седжуик въведе по-опростена версия на червено-черно дърво наречена ляво-наклонено червено-черно дърво, чрез елиминирането на по-рано неуточнена степен на свобода в изпълнението. LLRB поддържа допълнителен инвариант, че всички червени връзки трябва да са ляво-наклонени, освен по време на вмъкване и изтриване. Червено-черните дървета могат да бъдат направени изометрични до 2 – 3 дървета, или 2 – 4 дървета, за всяка последователност от операции. Изометрията на 2 – 4 дърветата е описана през 1978 г. от Седжуик. С 2 – 4 дървета изометрията е решена чрез „обръщане на цвета“ (color-flip), съответстваща на раделяне, в което червеният цвят на два възела на децата науска децата и се движи към възела родител. Дървото на танго, вид дърво, оптимизиран за бързо търсене, обикновено [кога?] използва червено-черните дървета, като част от неговата структура от данни.

Операции[редактиране | редактиране на кода]

Операциите „само за четене“ (read-only) на червено-черно дърво не се нуждаят от промяна от тези, използвани за двоични дървета за търсене (binary search trees), защото всяко червено-черно дърво е специален случай на просто двоично дърво за търсене. Въпреки това, прекият резултат на вмъкване или изтриване може да наруши свойствата на червено-черното дърво. Възстановяването на свойствата на червено-черно дърво изисква малък брой (Big-O_notation]] или амортизиран O(1)) промени в цвета (които са много бързи практически) и не повече от три ротации в дърветата (две за вмъкване). Въпреки че операциите вмъкване и изтриване са сложни, техните времена остават O(log n).

Вмъкване[редактиране | редактиране на кода]

Вмъкването започва чрез добавяне на възел както при всяко вмъкване при двоично дърво за търсене и чрез оцветяването му в червено. Докато в двоичното дърво за търсене винаги добавяме лист, в червено-черното дърво листата не съдържат информация, така че вместо това прибавяме червен вътрешен възел с две черни листа, на мястото на съществуващ черен лист.

Какво се случва след това зависи от цвета на другите близки възли. Терминът uncle node ще се използва за означаване на сродните на основния възел, както в човешките родословни дървета. Трябва да се отбележи, че:

свойство 3 (всички листа са черни) винаги се запазва.
свойство 4 (и двете деца на всеки червен възел са черни) е застрашено само чрез добавяне на червен възел, което пребоядисва черния възел в червено, или от ротация.
свойство 5 (всички пътища от даден възел до своите листни възли съдържат същия брой черни възли) е застрашено само от добавяне на черен възел, пребоядисване на червен възел в черен (или обратното), или от ротация.

Забележка:

Обозначението N ще бъде използвано за да означим текущият възел (оцветен в червено). В диаграмите N ще носи син контур. В началото това може да бъде новопоставен възел, но в цялата процедура може да се приложи рекурсивно и към други възли. С P ще означаваме бащата на N, с G неговият дядо, а с U – чичото на N. В последващите примери ролите и означенията на възлите се разменят, но въпреки това, всеки възел продължава да представлява същият възел, който е бил в началото на примера.
Номерираните триъгълници представляват поддърво с неопределена дълбочина. Черният кръг на върха на триъгълника означава, че черната височина на поддървото е по-голяма с единица сравнено с поддърво без такъв черен кръг.

Има няколко правила, които трябва да бъдат спазени при вмъкване в червено-черно дърво:

N e първият възел в червено-черното дърво
Родилетлят(P) на N е черен
Родителят(P) и чичото на N са червени.
N е добавен вдясно на лявото дете на дядото или N e добавен вляво на дясното дете на дядото (P е червено, а U е черно)
N е добавен вляво на лявото дете на дядото или N e добавен вдясно на дясното дете на дядото (P е червено, а U е черно)
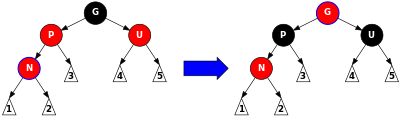
Диаграма за случай 1

Случай 1. Ако бащата на вмъкнатия елемент е ляво дете на дядото (този и другите случаи важат и за симетричните такива, само че с разменени указатели ляво/дясно и симетрични ротации) и е червен, чичото (чичо – другото дете на дядото) също е червен, то можем да сложим бащата и чичото да са черни, а дядото – червен (така не се нарушава свойство 4). Така нашия нов елемент има черен баща. По този начин обаче може дядото да наруши свойство 2 (ако неговият баща е червен).

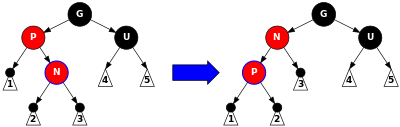
Случай 2. Елементът е дясно дете на баща си, бащата – ляво дете на дядото и е червен, а чичото – черен. В този случай правим лява ротация на бащата и директно го свеждаме до следващия случай (свойство 3 все още е нарушено).

Случай 3. Елементът е ляво дете на баща си, бащата – ляво дете на дядото и е червен, а чичото – черен. В този случай правим бащата черен, а дядото-червен и правим дясна ротация върху дядото. Така свойства 3 е удовлетворено, свойство 4 също (то не се нарушава в този и предишните случаи).

Изтриване[редактиране | редактиране на кода]

В обикновено двоично дърво за търсене, при изтриване на разклонение от две нелистови деца, намираме или максималния елемент на лявото поддърво

(което е предшественика подред) или минималния елемент на дясното поддърво (което е приемника подред) и преместваме стойността в изтритото разклонение.

След това изтриваме разклонението, стойността на което сме копирали, което трябва да има по-малко от две нелистови деца. (Нелистовите деца, за разлика от всички останали деца, са по-специални тук, защото за разлика от обикновените двоични дървета за търсене червено-черните дървета могат да има листни разклонения навсякъде, така че всички разклонения са или вътрешни разклонения с две деца или листни разклонения, по дефиниция, с нула деца. По функция вътрешните разклонения имащи по две листови деца са като листовите разклонения в обикновено бинарно дърво за търсене.) Поради това, че копирането на стойност не променя свойствата на червено-черното дърво, това свежда до проблема на изтриване на възел с поне едно нелистово дете. След като този проблем се разреши, решението му се прилага и в случая когато както разклонението, което искаме да изтрием има поне едно нелистово дете така и в случая, в който има има две нелистови деца.

Следователно, за остатъка от дискусията ние адресираме изтриването на разклонение с поне едно нелистово дете. Използваме М за маркираме разклонението, което ще бъде изтрито;С ще маркира избрано дете на М, което съще ще наричаме „неговото дете“. Ако М има нелистово дете, наричаме това „неговото дете“, С; иначе избираме едното от листата за „неговото дете“, С.

Ако М е червено разклонение, просто го заменяме със С, което трябва да е черно (от свойство 4).(Това може да се случи само когато М има две листови деца, защото ако червения възел М има черно, нелистово дете, от едната страна и само листово дете от другата, тогава бройката на черните разклонения от двете страни ще бъде различна, следователно дървото ще наруши 5-о свойство.) Всички пътища през изтрития възел просто ще преминават през един червен възел по-малко, родителят или детето на изтритото разклонение трябва да са черни, така че свойство 3(всички листа са черни) и свойство 4(и двете деца на всеки черен възел са черни) все още важат.

Следващ прост случай е когато М е черно, а С е червено. Премахването на черен възел би нарушило свойство 4 и 5(всички пътища от възел до листата му съдържат същата бройка черни възли.), но ако просто пребоядисаме С в черно и двете свойства ще се запазят.

Сложният случай е когато и М, и С са черни.(Това може да се случи само когато изтриваме черен възел, който има две две листови деца, защото ако черното разклонение М има черно нелистово дете от едната страна и само листово дете от другата, бройката на черни разклонения от двете страни ще бъде различна, следователно дървото няма да е валидно черно-червено дърво поради нарушаване на свойство 5.) Започваме със заместване на М с неговото дете С. Ще преименуваме С (в новата му позиция) с N, и роднината му (на новия родител-другото дете) S. (S е било роднина на М преди това.) В диаграмите надолу ще използваме Р за новия родител на N(стария родител на М), SL за лявото дете на S, и SR за дясното дете на S(S не може да бъде листо).

Забележки:

1. N ще бъде използвано за да се преименува текущия възел (оцветен в черно). В диаграмите N е със син контур. В началото, това е заместващият възел и листо, но цялата процедура може също да се приложи рекурсивно и към други възли (случай 3). В някои случаи ролите на етикетите и възлите се разменят, но във всеки случай всеки етикет представлява същия възел, който е представлявал в началото на случая.

2. Ако разклонение в дясната половина на диаграмата има син контур ще стане текущия контур в следващата итерация и там другите възли ще бъдат новообозначени като негови роднини. Всеки цвят показан в диаграмата е или предположен за случая си, или подразбран от тези предположения. Бялото представлява произволен цвят (черен или червен), но е същия и в двете части на диаграмата.

3. Нумериран триъгълник представлява поддърво от неопределена дълбочина. Черен кръг върху триъгълник означава че черната височина на поддърво и по-голяма с едно от поддърво без този кръг.

Ако и двете N, и истинският му родител са черни, тогава изтриването на този родител поражда пътищата, които преминават през N да имат един черен възел по-малко от пътищата които не преминават. След като това нарушава свойство 5, дървото трябва да се балансира отново. Има няколко случая да се вземат в предвид:

Случай 1. N е нов корен. Премахваме един черен възел от всяка пътека, следователно новия корен е черен, така свойствата са запазени.

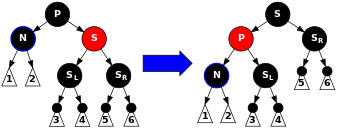
Случай 2. S e червен. В този случай разменяме цветовете на P и S и извършваме лява ротация на бащата. P очевидно трябва да е бил черен, тъй като е имал червено дете (S). Въпреки че всички пътеки имат същия брой черни възли, сега N има черен брат, което го свежда до случаи 3, 4 или 5 (новия брат е черен, понеже е бил дете на червения S). (В следващите случаи означаваме новия брат на N да е S).

Случай 3. P, S и децата на S са черни. В този случай просто пребоядисваме S да е червен. Резултатът е, че всички пътища, които минават през S, които са точно тези пътища, които не минават през N, имат един черен възел по-малко. Обаче сега всички пътища, които минават през P имат един черен възел по-малко от пътищата, които не минават през P, така че свойство 4 все още е нарушено. За да оправим това, прилагаме случай 1 върху P.

Случай 4. S и децата на S са черни, но P е червен. В този случай просто разменяме цветовете на S и P. Това не оказва влияние върху броя черни възли в пътищата, които не минават през N, но добавя черен възел в пътищата, които минават през N и така компенсира за изтрития възел.

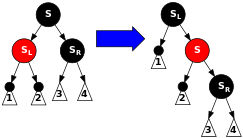
Случай 5. S е черен, лявото дете на S е червено, а дясното – черно (и N e ляво дете на баща си). В този случай извършваме дясна ротация върху S, така че лявото дете на S става баща на S и брат на N. След това разменяме цветовете на S и новия му баща. Всички пътища все още имат същия брой черни възли, но сега N има черен брат, чието дясно дете е червено и попадаме в случай 5.

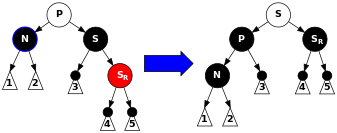
Случай 6. S е черен, дясното дете на S е червено и N е лявото дете на P(P e черен или червен). В този случай извършваме лява ротация върху P, така че S става баща на P. Корена на поддървото запазва цвета си, така че свойства 3 и 4 се запазват. Обаче N има допълнителен черен предшественик: или P е станал черен, или е бил черен и S e добавен като черен дядо. Така пътеките през N минават през един черен възел повече. Ако обаче пътя не минава през N, има две възможности:

Минава през брата на N. Следователно трябва да минава през S и Р, но те само са си разменили цветовете, следователно този път съдържа същия брой черни възли.
Минава през новия чичо на N (дясното дете на S). Следователно преди това е минавал през S, бащата на S и дясното дете на S но сега минава само през S, който има същия цвят като предишния му баща и дясното дете на S, което е променено от червено на черно, следователно този път минава през същия брой черни възли.

^[3]

Източници[редактиране | редактиране на кода]

↑ ^а ^б ^в ^г ^д ^е James Paton. Red-Black Trees
↑ Mehlhorn, Kurt, Sanders, Peter. Algorithms and Data Structures: The Basic Toolbox. Springer, Berlin/Heidelberg, 2008. ISBN 978-3-540-77977-3. DOI:10.1007/978-3-540-77978-0. с. 154 – 165. p. 155.
↑ Red–Black Trees // Introduction to Algorithms. second. MIT Press, 2001. ISBN 0-262-03293-7. с. 273 – 301.

Тази страница частично или изцяло представлява превод на страницата Red–black tree в Уикипедия на английски. Оригиналният текст, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за съдържание, създадено преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналната страница, както и на преводната страница, за да видите списъка на съавторите.

ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни.

[wiscurl-1] а ^б ^в ^г ^д ^е James Paton. Red-Black Trees

[2] Mehlhorn, Kurt, Sanders, Peter. Algorithms and Data Structures: The Basic Toolbox. Springer, Berlin/Heidelberg, 2008. ISBN 978-3-540-77977-3. DOI:10.1007/978-3-540-77978-0. с. 154 – 165. p. 155.

[:0-3] Red–Black Trees // Introduction to Algorithms. second. MIT Press, 2001. ISBN 0-262-03293-7. с. 273 – 301.

[1]

[2]

[3]