Числа на Фибоначи

Числата на Фибоначи в математиката образуват редица, която се дефинира рекурсивно по следния начин:

F(0) = 0
F(1) = 1
F(n) = F(n-1) + F(n-2)

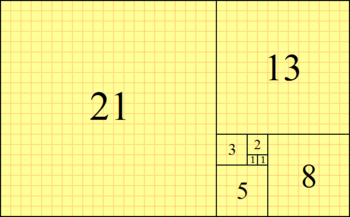
Започва се с 0 и 1, а всеки следващ член на редицата се получава като сума на предходните два. Първите числа на Фибоначи са:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …

Ето някои от основните свойства на числата на Фибоначи:

[F(n),F(m)]=F[(m,n)] т.е. НОД на числата F(n) и F(m) e число на Фибоначи с индекс НОД(m,n)

F(n+k)=F(k-1)*F(n) + F(k)*F(n+1)

F(k)/F(kn) за произволно n

Отношенията ${\frac {F_{n+1}}{F_{n}}}$ са приближени дроби на златното сечение φ и по-специално $\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\phi$ .

Числата на Фибоначи могат да се бележат и с u(n).

Произход

Италианският математик Леонардо Фибоначи публикува през 1202 г. редица от числа, всяко от които се получава като сума от предходните две, като първите две числа са 0 и 1: 0, 1, 1, 2, 3, 5, 8, 13, 21,… Той е научил за тази редица от числа по време на пътешествията си в страните от тогавашния Изток и редицата е била наречена на негово име, защото я е популяризирал.

Оказва се, че колкото по-големи са числата от редицата на Фибоначи, толкова отношението на двете последни числа се приближава до 'златното сечение' и при граничен преход (при безкраен брой числа в редицата) става равно на 'златното сечение'.

Често редицата на Фибоначи се свързва и със следната задача: Чифт зайци (мъжки и женски екземпляр) могат да произведат за единица време (напр. един месец) нов чифт зайци, които продължават да се размножават (в класическата задача на Фибоначи на новородения чифт зайци са му необходими два месеца, за да дадат първото си поколение, след което продължават да се размножават всеки месец). Колко е броят на живите чифтове зайци след определено време, ако никой не унищожава зайците? Отговорът се дава от последното число в редицата на Фибоначи. Разбира се, тази задача е чисто илюстративна.

Оказва се обаче, че твърде много закономерности, наблюдавани в природата и в поведението на човека, могат да се опишат, макар и с някаква по-малка или по-голяма грешка, с числа от редицата на Фибоначи, въпреки че в някои случаи това обяснение може да изглежда преднамерено.

Всъщност алгоритъмът за образуване на поредното число от редицата на Фибоначи изразява факта, че следствието (последното число от реда) зависи от предисторията (причините) по конкретния за тази редица начин, а именно: последното число е сума от двете предходни числа. Така този алгоритъм се включва в категорията на т. нар. рекурентни формули. Доколко с алгоритъма на 'златното сечение' могат да се обяснят природни и човешки феномени зависи именно от това, доколко тези феномени се подчиняват на горната проста и същевременно съответстваща добре на 'здравия разум' рекурентна зависимост на следствието от причините, които го пораждат. До Фибоначи основните алгоритми за описване на възпроизвеждащи формули са били аритметичната и геометричната прогресия.

Първите 100 числа на Фибоначи

пореден номер | число на Фибоначи

           1 |                     1
           2 |                     1
           3 |                     2
           4 |                     3
           5 |                     5
           6 |                     8
           7 |                    13
           8 |                    21
           9 |                    34
          10 |                    55
          11 |                    89
          12 |                   144
          13 |                   233
          14 |                   377
          15 |                   610
          16 |                   987
          17 |                  1597
          18 |                  2584
          19 |                  4181
          20 |                  6765
          21 |                 10946
          22 |                 17711
          23 |                 28657
          24 |                 46368
          25 |                 75025
          26 |                121393
          27 |                196418
          28 |                317811
          29 |                514229
          30 |                832040
          31 |               1346269
          32 |               2178309
          33 |               3524578
          34 |               5702887
          35 |               9227465
          36 |              14930352
          37 |              24157817
          38 |              39088169
          39 |              63245986
          40 |             102334155
          41 |             165580141
          42 |             267914296
          43 |             433494437
          44 |             701408733
          45 |            1134903170
          46 |            1836311903
          47 |            2971215073
          48 |            4807526976
          49 |            7778742049
          50 |           12586269025
          51 |           20365011074
          52 |           32951280099
          53 |           53316291173
          54 |           86267571272
          55 |          139583862445
          56 |          225851433717
          57 |          365435296162
          58 |          591286729879
          59 |          956722026041
          60 |         1548008755920
          61 |         2504730781961
          62 |         4052739537881
          63 |         6557470319842
          64 |        10610209857723
          65 |        17167680177565
          66 |        27777890035288
          67 |        44945570212853
          68 |        72723460248141
          69 |       117669030460994
          70 |       190392490709135
          71 |       308061521170129
          72 |       498454011879264
          73 |       806515533049393
          74 |      1304969544928657
          75 |      2111485077978050
          76 |      3416454622906707
          77 |      5527939700884757
          78 |      8944394323791464
          79 |     14472334024676221
          80 |     23416728348467685
          81 |     37889062373143906
          82 |     61305790721611591
          83 |     99194853094755497
          84 |    160500643816367088
          85 |    259695496911122585
          86 |    420196140727489673
          87 |    679891637638612258
          88 |   1100087778366101931
          89 |   1779979416004714189
          90 |   2880067194370816120
          91 |   4660046610375530309
          92 |   7540113804746346429
          93 |  12200160415121876738
          94 |  19740274219868223167
          95 |  31940434634990099805
          96 |  51680708854858323072
          97 |  83621143489848422977
          98 | 135301852344706746049
          99 | 218922995834555169026
         100 | 354224848179261915075

Външни препратки

Сайт с информация за числото Фи ((en))

Категория:Числови редици