Бутилка на Клайн

Модел на бутилка на Клайн в тримерно пространство

Бутилка на Клайн в математиката е двумерна повърхнина, която има само една страна, т.е. при нея не може да се разграничат „вътрешна“ от „външна“ страна. Тя не може да бъде конструирана в по-ниско от четиримерното пространство, макар че идея за нея може да бъде придобита от двумерните и тримерните ѝ изображения.

За първи път обектът е описан от немския математик Феликс Клайн през 1882 г. Първоначално Клайн го нарича "повърхнина" ("Fläche"), което грешно е превеждано на английски като "бутилка" ("Flasche"). Тази грешка обаче лесно се обяснява и с известното изображение на повърхнината, което прилича на бутилка, чието дъно с дупка е закривено и минавайки през стената на бутилката отново се слива с нейното гърло.

В топологията бутилката на Клайн е двумерно затворено неориентируемо многообразие с ойлерова характеристика нула.

Свойства и формулно представяне

Топологическа конструкция на бутилката на Клайн

Бутилката на Клайн е пример за повърхнина, която е едновременно едностранна и затворена. По подобие на листа на Мьобиус, бутилката е двумерно многообразие - диференцируемо и неориентируемо (т.е. такова, за което понятията ляво и дясно не са дефинирани). За разлика от листа на Мьобиус, бутилката е затворено многообразие - компактно и без граница. И докато листът на Мьобиус може да се реализира на практика в тримерното пространство, бутилката на Клайн не може. Тя обаче може да бъде успешно конструирана в четиримерно пространство, при което няма да се получи самопресичането и неизбежния отвор в повърхнината, които налагат ограниченията на двумерните и тримерните ѝ изображения.

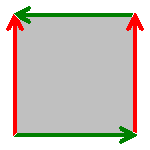
Топологически, Бутилката на Клайн се получава от квадрат [0,1] × [0,1] посредством отъждествяване на точките $(x, -1)$ с $(-x, 1)$ и на $(-1, y)$ с $(1, y)$. Така отъждествяването на страните на квадрата $x = \pm 1$ става „с усукване“, а на $y = \pm 1$ - „без усукване“.

Уравнението ѝ се задава с уравнението:

$(x^2 + y^2 + z^2 + 2y - 1)[(x^2 + y^2 + z^2 - 2y - 1) - 8z^2] + 16xz(x^2 + y^2 + z^2 - 2y - 1) = 0$

Бутилка на Клайн, представена чрез лист на Мьобиус

Друг вариант за конструирането на бутилката е, като се сгъне по дължина един лист на Мьобиус и ръбовете му се слепят. Обратно, чрез разрязване на бутилка на Клайн може да се получи отново лист на Мьобиус. В това си представяне бутилката на Клайн има следната проста параметризация:

$\begin{cases} x = (r + \ cos \frac{u}{2} \sin v - \sin \frac{u}{2} \sin 2v) \cos u \\ y = (r + \ cos \frac{u}{2} \sin v - \sin \frac{u}{2} \sin 2v) \sin u \\ z = \sin \frac{u}{2} \sin v + \cos \frac{u}{2} \sin 2v) \end{cases}$

При това представяне самопресичащата се окръжност е геометрична окръжност в равнината XY. Тук положителната константа r е радиусът на окръжността. Параметърът u задава ъгъла в равнината XY, а v фиксира положението спрямо сечението с форма на осморка.

Любопитно

• В телевизионния сериал "Футурама" на една полица е показана бира марка Клайн. Бутилката ѝ, естествено, е бутилка на Клайн.
• В Британския музей на науката е изложена красива колекция от тримерни модели на бутилката на Клайн от ръчно духано стъкло.

Вижте също

• Лист на Мьобиус
• Триъгълник на Пенроуз

Външни препратки

• Страница за бутилката на Клайн на сайта на Система Mathematica
• Конструкция на бутилка на Клайн