Потенциална яма
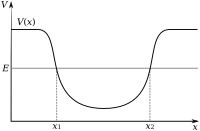
Потенциална яма се нарича диапазонът от енергии около локален минимум на потенциалната енергия. Потенциалната яма се характеризира с широчина и потенциална енергия (потенциал) . Когато едно тяло има потенциална енергия Е, по-ниска от и не може да получи допълнително енергия, се казва, че тялото е „уловено“ в ямата. Такъв пример за потенциална яма е например неутрон в атомно ядро. Ако към системата от тела се добави допълнително енергия така, че локалният минимум бъде надхвърлен, е възможно тялото да напусне ямата и потенциалната му енергия да се превърне в кинетична.
Противоположното понятие на потенциална яма е потенциална бариера – диапазонът от енергии около локален максимум на потенциалната енергия.
Една образна представа на двумерна потенциална повърхност е земната повърхност. Ако си представим пейзажа като съвкупност от долини и хълмове, потенциалната яма ще бъде долина, заобиколена отвсякъде с по-високи терени и евентуално пълна с вода (езеро), като водата не може да изтече към по-нисък минимум. Глобалният минимум в случая е морското равнище.
В квантовата механика обаче е възможно (има определена, макар и малка вероятност) частица с по-малка енергия да премине през потенциална бариера (виж тунелен преход).
Безкрайно дълбока потенциална яма[редактиране | редактиране на кода]
За безкрайно дълбока потенциална яма с широчина и потенциална енергия (потенциал) (тя може да се онагледи като кутия с твърди стени, в която елементарните частици изпитват еластични удари със стените: например електрони в метал, виж фиг. 1) може да се запише:
За област , уравнението на Шрьодингер има следното решение:
,
където е вълновата функция, а n=1,2,3,.. са възможните енергийни нива в ямата.
Източници[редактиране | редактиране на кода]
- Douglas C. Giancoli. Physik. Pearson Studium, 2006.









