Изолирана точка
Облик
За информацията в тази статия или раздел не са посочени източници. Въпросната информация може да е непълна, неточна или изцяло невярна. Имайте предвид, че това може да стане причина за изтриването на цялата статия или раздел. |
Тази статия се нуждае от подобрение. Необходимо е: ДОРАЗРАБОТВАНЕ, КРИТИЧЕН ПРОЧИТ И ПРИВЕЖДАНЕ В ЕНЦИКЛОПЕДИЧЕН ВИД.. Ако желаете да помогнете на Уикипедия, използвайте опцията редактиране в горното меню над статията, за да нанесете нужните корекции. |
В топологията елемент в топологично пространство се нарича изолирана точка на , ако съществува отворено множество . От дефиницията следва непосредствено, че един елемент е изолирана точка тогава и само тогава, когато не е точка на сгъстяване.
В едно метрическо пространство точката се нарича изолирана, ако съществува -околоност на , за която .
Примери
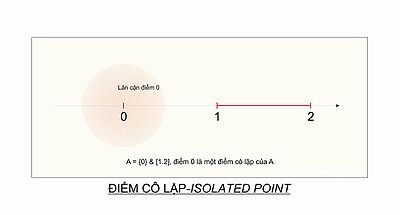
[редактиране | редактиране на кода]- В множеството числото 0 е изолирана точка.
- В множеството всеки елемент е изолирана точка, с изключение на нулата.
- В множеството на естествените числа всички точки са изолирани.
- (В примери 1.-3. се подразбира, че е избрана евклидовата метрика.)
Тази статия за математически обект все още е мъниче. Помогнете на Уикипедия, като я редактирате и разширите.











![{\displaystyle A=\{0\}\cup [1,2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bbddfd3db81d8d0a085f79b267d9f99a15efc5c)


