Квадрат (алгебра)

Квадратът на дадено число е алгебрична величина, равняваща се на произведението на числото със самото него.[1] Действието, описващо получаването на този резултат, се нарича повдигане на квадрат и е идентично със степенуване на степен 2. Аналогично на другите форми на степенуване, повдигането на квадрат се обозначава с горен индекс 2 – например квадратът на 3 може да се запише като 32 и се равнява на числото 9. Важно свойство на повдигането на квадрат е, че квадратът на всяко число x е равен на квадрата на неговото противоположно число −x, като по този начин е изпълнено тъждеството x2 = (−x)2.
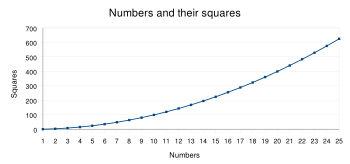
Числовата редица от квадратите на първите 50 цели числа (редица A000290 в ИЕЧР) има следния вид: [2]
- 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116 , 2209, 2304, 2401, 2500.
Исторически естествените числа от тази редица са били наричани „квадратни“.
Начини за представяне
[редактиране | редактиране на кода]Квадратът на естественото число може да се представи като:
- Сума от първите нечетни числа:
Примери:
- 1:
- 2:
- 3:
- 4:
- 5:
- 6:
- 7:
- …
- Сбор от числото и удвоената сума на естествените числа преди него:
Примери:
- 1:
- 2:
- 3:
- 4:
- 5:
- 6:
- …
Сумата от квадратите на първите естествени числа се изчислява по формулата:
Бележки и източници
[редактиране | редактиране на кода]- ↑ Squares and Square Roots in Algebra.
- ↑ N. J. A. Sloane – The On-Line Encyclopedia of Integer Sequences, 1964.


















