Кубоктаедър

Кубоктаедър е многостен, едно от тринадесетте Архимедови тела. Повърхнината му се състои от 6 квадрата и 8 равностранни триъгълника, като общия брой на стените е 14. Има 12 идентични върха, в които се срещат по две триъгълни и две квадратни стени. Има 24 идентични ръба, разделящи триъгълна от квадратна стена. До всеки връх достигат 4 ръба.
Кубоктаедърът може да се разглежда като получен с отсичането на върховете, било на куб, било на октаедър, до средата на ръбовете, които водят към тях.

Кубоктаедърът също може да се разглежда като получен с отсичането на ръбовете на тетраедър. Този метод не е така интуитивно ясен както предходните, тъй като тетраедърът има различна симетрия от тази куба или октаедъра. Обаче ако четирите различни оси на симетрия на тетраедъра се групират в двойки, получават се шест различни комбинации, които съвпадат с посоките на един тримерен координатен кръст. (Това е същото като наблюдението, че в куба може да се впише тетраедър, чиито ръбове да лежат в стените му.) При метода с отсичане на ръбовете от тетраедър, шестте негови ръба стават шестте квадратни стени на кубоктаедъра, на мястото на четирите върха се появяват 4 триъгълника и едновременно с това от стените остават още четири – общо осем.
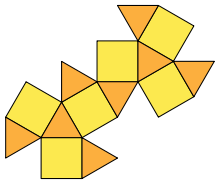
Най-голямото сечение на кубоктаедъра е правилен шестоъгълник. Това се съобразява лесно с разглеждането развивката. Така, кубоктаедърът може да бъде видян и като съединяване на два „купола“ с триъгълен покрив и стени, алтернативно квадрати и триъгълници.
Дуален на кубоктаедъра е ромбичният додекаедър.
При кубоктаедър с дължина на ръба a, лицето на повърхнината S и обемът V са съответно:
Разположението на върховете и ръбовете в кубоктаедъра се повтарят и при два неизпъкнали правилни многостена, кубохемиоктаедър и октохемиоктаедър. Тези две тела могат да се разглеждат като получени съответно от 6 правилни квадратни пирамиди или 8 тетраедъра, съединени по ръбовете към общ център.
 Кубоктаедър |
 Кубохемиоктаедър |
 Октохемиоктаедър |


