Тетраедър

Тази статия е за платоновото тяло. За многостена по брой на стени вижте Четиристен.

---

Анимация на правилен тетраедър

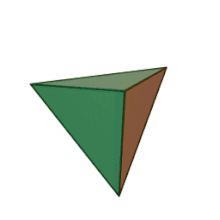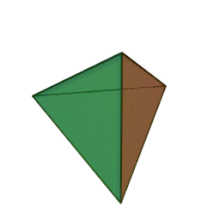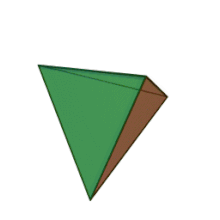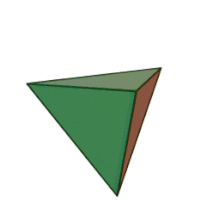
Тетраедърът е вид многостен с формата на триъгълна пирамида. Има 4 върха, 6 ръба и четири стени. Неговите разновидности могат да имат различна степен на симетрия, а тя е най-висока при правилния тетраедър, чиито стени са равностранни триъгълници и той е едно от петте платонови тела.

По-ниска симетрия имат:

• правилната триъгълна пирамида: трите стени са равнобедрени триъгълници, а основата – равностранен
• тетрагонален, ромбичен, дигонален и обикновен дисфеноид
• усукан тетраедър
• правоъгълен тетраедър: три ръба към един връх са перпендикулярни по двойки – съответните стени са правоъгълни триъгълници.

Обем на тетраедър

Ако четирите върха са точките, означени A, B, C и D, то обемът е:

$V={\frac {1}{6}}\left|det({\overrightarrow {AB}},{\overrightarrow {AC}},{\overrightarrow {AD}})\right|$

Ако основата е триъгълник с площ $B$ и съответната височина $h$, то обемът е:

$V={\frac {1}{3}}Bh$

Правилен тетраедър

Ако ръбът на правилен тетраедър е с дължина $a$,

• околната повърхност е: $A={\sqrt {3}}a^{2}$
• височината е: $H={\sqrt {\frac {2}{3}}}a={{\sqrt {6}} \over 3}a$
• обемът: $V={\tfrac {1}{12}}{\sqrt {2}}a^{3}$

Свойства

Tетраедър, вложен в куб

Върховете на правилен тетраедър лежат върху сфера. Той може също да бъде вложен и в куб, като ръбовете му са различните диагонали върху срещуположни страни.

Квадратно сечение на тетраедър

Средното сечение на куба, което е квадрат, се пренамира очертано от средите на четири страни на вложения тетраедър. Всичките 6 средни точки задават октаедъра, който е дуален на куба.

Вижте също

• Тетраедрално число
• Тристен
• Триъгълник
• Пентахорон
• Квадратна пирамида