Икосаедър

Правилен икосаедър

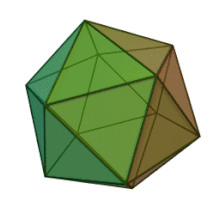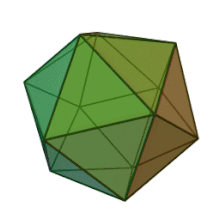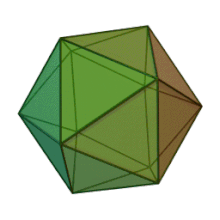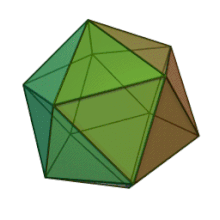
Икосаедърът (на старогръцки: εἴκοσι - 20 и на старогръцки: ἕδρον – основа) е геометрическо тяло с двадесет стени, т.е. „двадесетостен“. Правилният икосаедър е платоново тяло и делтаедър: той има 20 триъгълни стени, 12 върха и 30 ръба. Дуалният многостен е додекаедър.

Правилен икосаедър

При дължина на ръба a, площта S, обемът V, радиусите на вписаната и описаната сфери, съответно r и R, се дават с формулите:

площ: $S=5a^{2}{\sqrt {3}}$

обем: $V={\begin{matrix}{5 \over 12}\end{matrix}}(3+{\sqrt {5}})a^{3}$

радиус на вписаната сфера: $r={\begin{matrix}{1 \over {4{\sqrt {3}}}}\end{matrix}}(3+{\sqrt {5}})a$

радиус на описаната сфера: $R={\begin{matrix}{1 \over 4}\end{matrix}}{\sqrt {2(5+{\sqrt {5}})}}a$

Икосаедър вписан в куб

Икосаедър може да се впише в куб, така че всичките му върхове, общо 6 двойки, да лежат върху шестте стени. При това могат лесно да се съобразят стойностите за техните координати:

$$(\pm \varphi ,\pm 1,0)\,,\quad (\pm 1,0,\pm \varphi )\quad {\text{,}}\quad (0,\pm \varphi ,\pm 1)$$

като φ означава стойността на златното сечение, т.е. (1+√5)/2, а дължината на ръбовете е приета за 2.

История

Традиционно откритието или изобретяването на икосаедъра се приписва на древногръцкия математик Теетет. Основание за това дава първото пояснение (схолия) към кн. 13 на 'Елементи'. Автентичността на текста в това място обаче подлежи на съмнение. Спекулира се дали по-рано икосаедърът не е бил известен в древен Египет. За разлика от додекаедъра, който се разпознава в минерални образувания, икосаедърът не е имал естествен първообраз. Вируси и микроорганизми имат икосаедрична (или псевдоикосаедрична) форма, също както атомни клъстери на елемента бор, но те са ненаблюдаеми с невъоръжено око.

Джонсонови тела с 20 стени

Шест от Джонсоновите тела са неправилни икосаедри:

J22	J35	J36	J59	J60	J92
Жироудължен триъгълен купол	Удължен триъгълен ортобикупол ]	Удължен триъгълен жиробикупол	Парабинадстроен додекаедър	Метабинадстроен додекаедър	Триъгълна хебесфероротонда
16 триъгълника 3 квадрата   1 шестоъгълник	8 триъгълника 12 квадрата	8 триъгълника 12 квадрата	10 триъгълника   10 петоъгълника	10 триъгълника   10 петоъгълника	13 триъгълника 3 квадрата 3 петоъгълника 1 шестоъгълник

Звездовидни икосаедри

Тринадесет стелации на икосаедъра

• малък триамбичен икосаедър (1)
• съединение от пет октаедъра (2)
• съединение от пет тетраедъра (12)
• съединение от десет тетраедъра (13)
• изкопан додекаедър (30)
• голям икосаедър (45)
• бодлостен (58)

Източници

Тази статия, свързана с математика, все още е мъниче. Помогнете на Уикипедия, като я редактирате и разширите.