Сфера
Тази статия се нуждае от подобрение. Необходимо е: редактиране на препратки към рускоезичната Уикипедия. Ако желаете да помогнете на Уикипедия, използвайте опцията редактиране в горното меню над статията, за да нанесете нужните корекции. |
Сфера е геометрична повърхност, която се дефинира като множество от точки, намиращи се на дадено разстояние от определена точка. Тази точка се нарича център на сферата, а разстоянието до точките от сферата се нарича неин радиус.[1] Сферата се получава също чрез въртене в пространството на окръжност около неин диаметър; центърът на тази окръжност е център и на сферата, а радиусът ѝ е равен на радиуса на сферата.

Всяка отсечка, която свързва центъра на сферата с произволна нейна точка има дължина, равна на радиуса и също се нарича радиус. Сфера с радиус 1 се нарича единична сфера.
Кълбо и сфера[редактиране | редактиране на кода]
Обединението от точките върху сферата и тези във вътрешността ѝ се нарича кълбо. Сферата е повърхността на геометричното тяло кълбо.
Общият случай на сфера в n-мерно пространство е повърхнина с n – 1 измерения. Вътрешността ѝ съответно е n-мерно кълбо.
Сфера се отнася към кълбо в тримерното пространство, както окръжност към кръг в двумерното.
Взаимни положения на права, равнина и сфера[редактиране | редактиране на кода]

Всяка права може да има с дадена сфера 0, 1 или 2 общи точки.
Когато правата има 2 общи точки със сферата, тя е секуща. Отсечката, чиито краища са двете пресечни точки, се нарича хорда на сферата. Хорда, минаваща през центъра, се нарича диаметър и той е равен на два радиуса . Разстоянието между двете пресечни точки по повърхността на сферата се нарича дъга на сферата.


Когато правата има само една обща точка със сферата, тя се нарича допирателна, а общата точка се нарича допирна точка. Всяка допирателна е перпендикулярна на радиуса, който свързва центъра на сферата с допирната точка. Валидно е и обратното твърдение. Всички допирателни към сфера във фиксирана нейна точка лежат в една равнина, която се нарича допирателна равнина. Например, сфера, поставена върху равна основа се допира до нея в една точка.

Сфери на Данделен[редактиране | редактиране на кода]
В геометрията сферите на Данделен са една или две сфери, които са допирателни както към равнина, така и към конус, който се пресича от равнината. Пресечната част на конуса и равнината е конично сечение, а точката, в която една от двете сфери се допира до равнината, е фокус на коничното сечение. Затова сферите на Данделен понякога се наричат също фокални сфери. [2]
Ако коничното сечение е елипса, съществуват две такива сфери в същия конус, които се допират до секущата равнина от двете ѝ страни, както е показано на чертежа – допирните им точки и са фокуси на елипсата. Когато сечението е хипербола, едната сфера е разположена в дадения конус, а втората – в симетричен конус на дадения относно върха му. Допирните точки са фокуси на хиперболата. В случая, когато коничното сечение е парабола, съществува само една сфера, която се допира до секущата равнина във фокуса на параболата.
Kръгови сечения[редактиране | редактиране на кода]


Всяка равнина, която не е допирателна към сферата, или няма общи точки с нея, или я пресича по окръжност. Тази окръжност се нарича голяма окръжност, когато секущата равнина минава през центъра на сферата, и малка окръжност, когато тя не минава през центъра.
Ако сечението е окръжност, то може да бъде записано в параметричен вид:
(вижте Равнинно сечение на елипсоид.)
Пресичане на сфера с повърхност на въртене, чиято ос минава през центъра на сферата, се състои от окръжности и/или точки.
На фигурата сфера пресича цилиндър в две окръжности. Ако диаметрите сферата и цилиндъра са равни, сферата е вписана в цилиндъра и се допира до него в контактна окръжност.
Ротационен елипсоид със същия център като сферата и голяма ос като диаметъра на сферата би допирал сферата в две точки (върхове), които са краищата на голямата ос.
Това свойство се използва в дескриптивната геометрия за конструиране на точки върху пресечната крива на повърхности на въртене (вижте метода на спомагателната сфера).

Криви върху сфера[редактиране | редактиране на кода]
Локсодрома[редактиране | редактиране на кода]
В навигацията локсодромата е дъга, пресичаща всички меридиани под един и същи ъгъл. Локсодромите са същите като правите линии в Меркаторовата проекция. Локсодромата не е сферична спирала. С изключение на някои прости случаи, формулата на локсодромата е сложна. В Морска навигация движението по локсодрома отговаря на движение по постоянен истински или магнитен курс.
Клелия[редактиране | редактиране на кода]
Линията клелия е крива върху сфера, за която географската дължина и географската ширина отговарят на уравнението
- .
Специални случаи са: кривата на Вивиани () и сферичните спирали () като сейфертовата спирала. Пътят на сателитите в полярна орбита се приближава до клелия.


Сферични коники[редактиране | редактиране на кода]

Аналогът на коничното сечение върху сферата е сферична конична част, биквадратна крива, която може да бъде дефинирана по няколко еквивалентни начина, включително:
- като пресечната точка на сфера с квадратен конус, чийто връх е центърът на сферата;
- като пресечна точка на сфера с елиптичен или хиперболичен цилиндър, чиято ос минава през центъра на сферата;
- като геометрично място на точки, чиято сума или разлика от разстоянията на голям кръг от двойка фокуси е постоянна.
Много теореми, отнасящи се до равнинни конични сечения, се отнасят и до сферичните конични сечения.
Сечение на сфера с по-обща повърхност[редактиране | редактиране на кода]
Ако една сфера е пресечена от друга повърхност, може да има по-сложни сферични криви.

Сфера – цилиндър[редактиране | редактиране на кода]
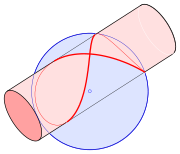
Сечението на сфера с уравнение и цилиндър с уравнение не е само един или два кръга. Това е решението на нелинейната система от уравнения
Графично се изразява с червената неявна крива на фигурата.
Части на сфера и кълбо[редактиране | редактиране на кода]
Всяка равнина, която пресича сфера, разделя сферичната повърхнина на две сферични шапки, а кълбото – на два сферични сегмента. Ако равнината минава през центъра на сферата, се получават 2 полусфери и 2 полукълба.
Ако две успоредни равнини пресичат сфера, те отсичат от сферичната повърхнина сферичен пояс, а от кълбото – сферичен слой.
Когато краят на един радиус описва окръжност по сферата, кълбото се разделя на два сферични сектора.
Две равнини през центъра на сферата я разделят на четири сферични двуъгълника, а кълбото – на четири сферични клина.
Две пресичащи се равнини, чиято пресечна линия лежи частично вътре в сферата, изрязват обект от сферата, чиято извита повърхност е лунната сфера.
Определения[редактиране | редактиране на кода]
Сферата е повърхност, образувана от въртене на кръг с половин оборот около всеки от неговите диаметри; това е много подобно на традиционното определение на сфера, дадено в „Елементи“ на Евклид. Тъй като кръгът е специален тип елипса, сферата е специален вид ротационен елипсоид. Заменяйки кръга с елипса, завъртяна около главната си ос, формата става издължен сфероид; завъртян около малката ос, сплескан сфероид. [3]
Дълго време ежедневният език е използвал думата „сфера“ за назоваване както на повърхността, така и на геометричното тяло, което тя ограничава. В наши дни освен прецизираните понятия „сфера“ за повърхността и „кълбо“ за геометричното тяло са формулирани и други определения, свързани със сферата: [4]
- Две антиподни точки са две диаметрално противоположни точки на сферата. Това е случаят с географските полюси на земната сфера.
- Голяма окръжност (кръг) е окръжност, начертана върху сферата и имаща същия радиус като сферата. Големият кръг винаги минава през две противоположни точки. Меридианите на земната сфера са големи окръжности. Паралелите също са окръжности, начертани върху сферата, но техните радиуси обикновено са по-малки от тези на сферата и тогава те не са големи окръжности. Единственият паралел, който е голяма окръжност, е екваторът.

- Сферичен капак е част от сфера, отрязана от пресичаща я равнина.
- Сферичен пояс (сферична зона) е част от сфера между две успоредни равнини.
- Сферичен слой е геометричното тяло, ограничено от две успоредни равнини, пресичащи сфера и сферичния пояс, който те определят.
- Сферичен сегмент е фигура, начертана върху сферата от два големи полукръга с еднакви краища.
- Сферичен клин е геометрично тристенно тяло, изрязано от кълбо от две пресичащи се равнини в кълбото. Двете му стени са равнинни, а третата е сферичен сегмент, подобно на резен от диня или портокал.



- Сферичен сектор или сферичен конус е геометрично тяло с конична околна повърхнина и сферична основа с формата на сферичен капак, изрязано от кълбо от радиус, чийто подвижен край описва окръжност.
- Сферична обвивка (куха сфера) е разликата между две концентрични сфери с различен радиус.


- Сферичен триъгълник е фигура, начертана върху сферата, образувана от три точки, свързани с дъги от големи кръгове.
- Сферичният многоъгълник е фигура, начертана върху сфера, образувана от няколко точки, свързани с дъги от кръгове.
Свойства[редактиране | редактиране на кода]
В своята книга „Геометрията и въображението“ Давид Хилберт и Стефан Кон-Восен описват 11 свойства на сферата и обсъждат дали тези свойства уникално определят сферата. [5] Има няколко свойства за равнината, която може да се разглежда като сфера с безкраен радиус. Тези свойства са:
- Всички точки на сферата са на едно и също разстояние от фиксирана точка. Също така съотношението на разстоянието на нейните точки от две фиксирани точки е постоянно.
- Първата част е обичайното определение на сферата и я определя еднозначно. Втората част може лесно да бъде изведена и следва подобен резултат за кръга на Аполоний Пергски. Тази втора част важи и за двумерното пространство.
- Контурите и равнинните сечения на сферата са кръгове.
- Това свойство дефинира сферата уникално.
- Сферата има постоянна ширина и постоянна обиколка.
- Ширината на повърхността е разстоянието между двойки успоредни допирателни равнини. Много други затворени изпъкнали повърхности имат постоянна ширина, например тялото на Майснер. Обиколката на повърхността е обиколката на границата на нейната ортогонална проекция върху равнина. Всяко от тези свойства предполага другото.

Нормален вектор към сфера, нормална равнина и нейното нормално сечение. Кривината на кривата на пресичане е секционната кривина. За сферата всяко нормално сечение през дадена точка ще бъде окръжност със същия радиус: радиусът на сферата. Това означава, че всяка точка от сферата ще бъде кръгова точка.
- Всички точки на една сфера са кръгови.
- Във всяка точка на повърхността нормалната посока е под прав ъгъл спрямо повърхността, защото на сферата това са линиите, излъчващи се от центъра на сферата. Пресечната точка на повърхността с равнина, която съдържа нормалата, ще образува крива, която се нарича нормално сечение, а кривината на тази крива е нормалната кривина. За повечето точки на повечето повърхности различните участъци ще имат различна кривина; максималната и минималната им стойност се наричат главни кривини. Всяка затворена повърхност ще има поне четири точки, наречени точки на закръгляне, кръгови точки или още пъпни точки (на френски омбилики). В тях всички секущи кривини са равни; по-специално главните кривини са равни. Пъпните точки могат да се разглеждат като точките, където повърхността е близка до сфера.
- За сферата кривините на всички нормални сечения са равни, така че всяка точка е пъпна. Сферата и равнината са единствените повърхности с това свойство.
- Сферата няма повърхност от центрове.
- За дадено нормално сечение съществува окръжност на кривина, която е равна на секционната кривина, допирателна е към повърхността и чиито централни линии лежат на нормалната линия. Например, двата центъра, съответстващи на максималната и минималната секционна кривина, се наричат фокални точки, а наборът от всички такива центрове образува фокалната повърхност.
- За повечето повърхности фокалната повърхност образува два листа, всеки от които е повърхност и се срещат в пъпни точки. Няколко случая са специални:
- * За канални повърхности единият лист образува крива, а другият лист е повърхност.
- * За конуси, цилиндри, тори и циклиди и двата листа образуват криви.
- * За сферата центърът на всеки оскулиращ кръг е в центъра на сферата и фокалната повърхност образува една точка. Това свойство е уникално за сферата.
- Всички геодезични на сферата са затворени криви.
- Геодезичните са криви на повърхност, които дават най-късото разстояние между две точки. Те са обобщение на понятието права линия в равнината. За сферата геодезичните са големи окръжности. Много други повърхности споделят това свойство.
- От всички твърди тела с даден обем, сферата е тази с най-малка повърхност; от всички твърди тела с дадена повърхност, сферата е тази с най-голям обем.
- Следва от изопериметрично неравенство. Сферата има най-малката площ от всички повърхности, ограничаващи даден обем; с други думи, от всички повърхности с дадена площ, сферата ограничава най-големия обем.
- Тези свойства определят сферата уникално и могат да се видят в сапунените мехурчета: сапуненият мехур ще обхване фиксиран обем, а повърхностното напрежение минимизира повърхността му за този обем. Следователно свободно плаващ сапунен мехур се доближава до сфера (въпреки че такива външни сили като гравитацията леко ще изкривят формата на балона). Може да се види и на планети и звезди, където гравитацията минимизира повърхността на големите небесни тела. Именно поради минимизирането на повърхността от силата на повърхностното напрежение, малките капки вода в безтегловност придобиват сферична форма.
- Сферата има най-малката обща средна кривина сред всички изпъкнали тела с дадена повърхност.
- Средната кривина е средната стойност на двете главни кривини, която е постоянна, тъй като двете главни кривини са постоянни във всички точки на сферата.
- Сферата има постоянна средна кривина.
- Сферата е единствената вградена повърхност, на която липсват граници или сингулярности с постоянна положителна средна кривина. Други такива потопени повърхности като минимални повърхности имат постоянна средна кривина.
- Сферата има постоянна положителна Гаусова кривина.
- Гаусова кривина е произведението на двете главни кривини. Това е присъщо свойство, което може да се определи чрез измерване на дължина и ъгли и е независимо от това как повърхността е вградена в пространството. Следователно, огъването на повърхност няма да промени гаусовата кривина, а други повърхности с постоянна положителна гаусова кривина могат да бъдат получени чрез изрязване на малък прорез в сферата и огъването ѝ. Всички тези други повърхности биха имали граници, а сферата е единствената повърхност, на която липсва граница с постоянна, положителна Гаусова кривина. Псевдосферата е пример за повърхност с постоянна отрицателна Гаусова кривина.
- Сферата се трансформира в себе си чрез трипараметърно семейство от твърди движения.
- Завъртането около която и да е ос на единична сфера в началото ще нанесе сферата върху себе си. Всяко завъртане около права през началото може да се изрази като комбинация от завъртания около трикоординатната ос (вижте ъгли на Ойлер). Следователно съществува трипараметърна фамилия ротации, така че всяка ротация трансформира сферата върху себе си; това семейство е ротационната група SO(3). Равнината е единствената друга повърхност с трипараметърно семейство от трансформации (транслации по осите x и y и ротации около началото). Кръговите цилиндри са единствените повърхности с двупараметрични семейства от твърди движения и повърхностите на въртене, а хеликоидите са единствените повърхности с еднопараметрично семейство.
Сферата е специален случай на елипсоид, в който и трите оси (полуоси, радиуси) са равни.
Една сфера се определя еднозначно от четири точки, които не са в една равнина. По-общо една сфера се определя уникално от четири условия като преминаване през точка, допирателна към равнина и т.н. [6] Това свойство е аналогично на свойството, че три неколинеарни точки определят уникална окръжност в равнина.
Следователно една сфера е еднозначно определена от (т.е. минава през) окръжност и точка, която не е в равнината на тази окръжност.
Сферата е глобално инвариантна при ротация, чиято ос минава през нейния център. [7]
Гравитационното поле на кълбо с маса , която е разпределена според радиална симетрия [т. е. по такъв начин, че всеки „сферичен слой“ (сфера с даден радиус, по-малък или равен на този на кълбото) на кълбото е хомогенен] е идентично, извън него, на това на точкова маса , която би била разположена в центъра на кълбото.
Съвкупност от сфери[редактиране | редактиране на кода]
Ако f(x, y, z) = 0 и g(x, y, z) = 0 са уравненията на две различни сфери, тогава
е уравнението на сфера за произволни стойности на параметрите s и t. Множеството от всички сфери, удовлетворяващи това уравнение, се нарича съвкупност от сфери, определени от първоначалните две сфери. В тази дефиниция се допуска сферата да бъде равнина (безкраен радиус, център в безкрайност) и ако и двете оригинални сфери са равнини, тогава всички сфери на съвкупността са равнини, в противен случай има само една равнина (радикалната равнина) в съвкупността. [8]


Координати, уравнения и неравенства[редактиране | редактиране на кода]
Координатите, уравненията и неравенствата на сферата и кълбото се разглеждат от аналитичната геометрия.
Когато центърът на сферата и съответното кълбо с радиус е в началото на тримерна правоъгълна координатна система Oxyz, координатите на точките на сферата удовлетворяват уравнението
- ,
а координатите на точките на кълбото удовлетворяват неравенството
- .
Ако центърът на сферата и кълбото е в произволна точка с координати , то уравнението на сферата е
- ,
а неравенството на кълбото:
- .
Тъй като може да се изрази като квадратичен полином, сферата е повърхност от втори ред – вид алгебрична повърхност, наричана още квадрика. [9]
Нека a, b, c, d, e са реални числа и a ≠ 0. Полага се
- .
Тогава уравнението
няма реални точки като решения, ако и се нарича уравнение на въображаема сфера.
Ако , единственото решение на уравнението е точката и уравнението се нарича уравнение на точкова сфера. И накрая, в случая , е уравнение на сфера с център точка и радиус . [10]
Ако a в горното уравнение е нула, тогава f(x, y, z) = 0 е уравнението на равнина. По този начин една равнина може да се разглежда като сфера с безкраен радиус, чийто център е точка в безкрайността. [8]
Във векторна форма уравнението на сферата се записва във вида
- , :
- ,
- ,
- или
- .
Точките на сферичната повърхност с радиус и център в началото могат да бъдат параметризирани чрез сферични координати, както следва:
с и .
Координатите на сфера в n-мерно линейно пространство с метрика скаларното произведение са свързани с уравнението:
- .
Координатите на съответното кълбо n-мерното линейно пространство удовлетворяват неравенството:

- .
Точките от сфера с радиус се представят параметрично чрез връзката между правоъгълни и сферични координати:
- ,
където са ъгловите координати в сферична координатна система (вижте също тригонометрична функция и сферични координати.) Ъглите съответстват съответно на географска ширина и дължина.
Съответните параметрични неравенства за кълбо са:
- .
Сфера с произволен радиус с център в началото на координатната система се описва със следното диференциално уравнение:
- .
Координати на сфера, преминаваща през зададени точки[редактиране | редактиране на кода]
През четири точки от пространството може да преминава единствена сфера с център
където:
Радиусът на сферата е
- .
Основни формули[редактиране | редактиране на кода]
Сфера[редактиране | редактиране на кода]

Обем[редактиране | редактиране на кода]
Обем на кълбо, ограничено от сфера с радиус и диаметър в триизмерното евклидово пространство:
- ,
или приблизително:
- .
Архимед за първи път извежда тази формула, като показва, че обемът вътре в една сфера е два пъти обемът между сферата и описания цилиндър около тази сфера (с височина и диаметър, равни на диаметъра на сферата). [11] Това може да се докаже чрез вписване на конус с върха надолу в полусфера, като се отбележи, че площта на напречното сечение на конуса плюс площта на напречното сечение на сферата е същата като площта на напречното сечение на описващия цилиндър, и прилагайки метода на неделимите. [12] Тази формула може също да бъде получена с помощта на интегрално смятане, т.е. дисково интегриране за сумиране на обемите на безкраен брой кръгли дискове с безкрайно малка дебелина, подредени един до друг и центрирани по оста от до , като се приеме, че сферата с радиус е центрирана в началото.
Доказателство за обем на сфера чрез изчисление
|
|---|
|
Обемните елементи имат елементарни обеми . За всяка стойност на , елементарният обем е равен на произведението от площта на напречното сечение на диска при и неговата дебелина :
Общият обем на кълбото в сферата е сумата от всички елементарни обеми:
В граничния случай → 0 [13] и това уравнение става:
За всяка дадена стойност на , координатите , и образуват правоъгълен триъгълник с връх в координатното начало и съгласно Питагоровата теорема:
Използването на тази замяна дава и от интегрирането се получава:
Същият резултат се получава ако елементарният обем се изрази в сферични координати: откъдето |
За повечето практически цели обемът вътре в сфера, вписана в куб, може да бъде приблизително равен на 52,36 % от обема на куба, тъй като , където е диаметърът на сферата, а също и дължината на страната на куба и π/6 ≈ 0,5236. Например сфера с диаметър 1 m има 52,36 % от обема на куб с дължина на ръба 1 m, или около 0,5236 m3.
Площ[редактиране | редактиране на кода]
Площ на сфера с радиус и диаметър в триизмерното евклидово пространство:
- .
Архимед първи извежда и тази формула [14] от факта, че проекцията към страничната повърхност на описан цилиндър запазва площта [15]. Друг подход за получаване на формулата идва от факта, че тя е равна на производната на формулата за обема по отношение на , тъй като общият обем вътре в сфера с радиус може да се разглежда като сумиране на повърхностната площ на безкраен брой от сферични обвивки с безкрайно малка дебелина, концентрично подредени една в друга от радиус 0 до радиус . При безкрайно малка дебелина несъответствието между вътрешната и външната повърхност на всяка дадена обвивка е безкрайно малко и елементарният обем при радиус е просто произведението на повърхността при радиус и безкрайно малката дебелина.
Площта на безкрайно малък елемент от повърхността на сферата (елементарна площ) в правоъгълни координати се определя от израза
- .
Алтернативно в сферични координати ширина и дължина елементарната площ е
- .
Доказателство за площ на сфера чрез изчисление
|
|---|
|
При всеки даден радиус , разглеждан като променлива, елементарният обем е равен на произведението от площта на повърхността при радиуса и дебелината на обвивката
Общият обем на тялото е сумата от всички елементарни обеми: В граничния случай доближава нулата [13] и това уравнение става: Замества се : Диференцират се двете страни на това уравнение спрямо :
Това съкратено се записва
където r сега се счита за фиксиран радиус на сферата. Общата площ на сферата може да бъде получена чрез интегрално сумиране на всички елементарни площи dS = r2 sin θ dθ dφ от повърхността ѝ:
|
Площта на повърхността спрямо масата на кълбото се нарича специфична площ на повърхността и може да бъде изразена от горните уравнения като
- ,
където е плътността (отношението на масата към обема).
Други формули[редактиране | редактиране на кода]
Пълен телесен ъгъл на сфера:
- стерадиана кв. градуса.
Двете главни кривини на сферата са равни: .
Гаусовата кривина на сфера е постоянна: .
Скаларната кривина на сферата е еднаква: .
Инерционният момент на еднородно кълбо с радиус , плътност и маса по отношение на ос, минаваща през неговия център, е:
- .
Инерционният момент на еднородна сфера с радиус и маса по отношение на ос, минаваща през нейния център, е
- .
Сферичен капак и пояс[редактиране | редактиране на кода]
От сфера с радиус чрез секуща равнина е отрязан сферичен капак с радиус на основата , височина и централен ъгъл .

Площта на сферичния капак се изчислява по формулите:
- ,
- ,
- .
Обемът на сферичния капак се определя от изразите:
- ,
- ,
- . [16]
Площта на сферичен пояс е
- ,
където е разстоянието между двете успоредни равнини, които пресичат сферата. Площта е същата като околната повърхнина на кръгъл цилиндър със същата височина, допирателна към сферата (описан цилиндър около сферата). Този забележителен резултат е демонстриран от Архимед в неговия трактат „За сферата и цилиндъра“. Според Цицерон Архимед поискал върху гробницата му да бъде гравирана сфера и очертаният от нея цилиндър в памет на този резултат.
Цилиндърът, описан около дадена сфера, има обем, равен на 1,5 пъти обема на сферата.
Сферичен сегмент и клин[редактиране | редактиране на кода]
От сфера (кълбо) с радиус чрез два секущи големи полукръга с общи полюси е отрязан сферичен сегмент (клин) с ъглова ширина на напречната дъга в радиани [rad].

Площта на сферичния сегмент се изчислява по формулата
- .
Повърхнината на сферичния клин е съставена от сферичния сегмент и два големи полукръга, следователно нейната площ е
- .
Обемът на сферичния клин се определя от израза
- ,
където е площта на сферичния сегмент, служеща за основа на клина.
Центърът на тежестта на сферичния сегмент е разположен по оста на симетрия на сегмента. Разстоянието му от центъра се определя от изразите: [17]
- за сферичен сегмент с безкрайно малка дебелина
- .
- за сферичен сегмент с двустенен ъгъл α е необходимо да се намери центърът на тежестта на дъгата на окръжност, върху която са всички центрове на тежестта на секторите с безкрайно малка дебелина
- .
Центърът на тежестта на сферичния клин е на три четвърти от отсечката, свързваща центъра на сферата с центъра на тежестта на сферичния сегмент: [18]
- .
Сферичен сектор[редактиране | редактиране на кода]
Когато радиусът на кълбо описва конична повърхност с връх в центъра на кълбото, той изрязва от него сферичен сектор, известен също като сферичен конус. Ако краят на радиуса се движи по малка окръжност от сферата, получава се кръгов сферичен сектор (конус). Той има основа сферичен капак с радиус на основата и височина и конична околна повърхнина. Това е триизмерният аналог на кръговия сектор.
Лицето на основата на сферичния сектор е площта на сферичния капак:

- ,
- .
Лицето на околната повърхнина се определя по формулата за околна повърхнина на прав кръгов конус:
- ,
- .
Лицето на пълната повърхнина на сферичния сектор е
- .
Обемът на сферичния конус се определя по формулата
- .
Геометрия на сфера[редактиране | редактиране на кода]
Окръжност, лежаща върху сфера, чийто център съвпада с центъра на сферата, се нарича голяма окръжност (голям кръг) на сферата. Големите кръгове са геодезически линии върху сферата; всеки два от тях се пресичат в две точки. С други думи, големите кръгове на сферата са аналози на прави линии в равнината, разстоянието между точките на сферата е дължината на дъгата на голямата окръжност, минаваща през тях. Ъгълът между правите в равнината съответства на двустенния ъгъл между равнините на големи кръгове. Много теореми на геометрията на равнината са валидни и в сферичната геометрия, има аналози на синусовата теорема, косинусовата теорема за сферични триъгълници. В същото време има много разлики, например в сферичен триъгълник сумата от ъглите винаги е по-голяма от 180 градуса, към трите признака за еднаквост на триъгълниците се добавя тяхната еднаквост по три ъгъла, сферичен триъгълник може да има два или дори три прави ъгъла – например сферичен триъгълник, образуван от екватора и меридианите 0° и 90°.
Разстояние между две точки на сфера[редактиране | редактиране на кода]
Ако са дадени сферичните координати на две точки, разстоянието между тях може да се намери, както следва:
- .
Ако обаче ъгълът не е даден между оста Z и вектора към точката на сферата, а между този вектор и равнината XY (както е обичайно в земните координати, дадени от географска ширина и географска дължина), тогава формулата ще бъде:
- .
В този случай се наричат географски ширини, а – географски дължини.
Сфера в области от математиката[редактиране | редактиране на кода]
Сферична геометрия[редактиране | редактиране на кода]
Голям кръг върху сфера
Основните елементи на равнинната геометрия на Евклид са точки и линии. На сферата точките се определят в обичайния смисъл. Аналогът на „линията“ е геодезичната, която е голяма окръжност; определящата характеристика на големия кръг е, че равнината, съдържаща всичките му точки, също минава през центъра на сферата. Измерването по дължината на дъгата показва, че най-късият път между две точки, разположени върху сферата, е по-късият сегмент от голямата окръжност, който включва точките.
Много теореми от класическата геометрия са валидни и за сферичната геометрия, но не всички, защото сферата не успява да удовлетвори някои от аксиомите на класическата геометрия, включително аксиомата за успоредните прави. В сферичната тригонометрия ъглите се определят между големи кръгове. Сферичната тригонометрия се различава от обикновената тригонометрия в много отношения. Например сумата от вътрешните ъгли на сферичен триъгълник винаги надвишава 180 градуса. Освен това всеки два подобни сферични триъгълника са еднакви.
Всяка двойка точки на сфера, която лежи на права линия през центъра на сферата (т. е. диаметъра), се наричат антиподни точки (полюси). Разстоянието между тях по сферата е точно половината от дължината на обиколката. Няма значение коя посока е избрана, разстоянието е радиусът на сферата × π. Всяка друга (т. е. неантиподна) двойка отделни точки на сфера
- лежи върху уникален голям кръг,
- сегментира се на една малка (т. е. по-къса) и една голяма (т. е. по-дълга) дъга, и
- дължината на малката дъга е най-късото разстояние между тях по сферата.
Сферичната геометрия е форма на елиптична геометрия, която заедно с хиперболичната геометрия съставлява неевклидова геометрия.
Диференциална геометрия[редактиране | редактиране на кода]
Сферата е гладка повърхност с постоянна Гаусова кривина във всяка точка, равна на 1/r2.[14] Според Гаусовата теорема на Егрегиум тази кривина е независима от вграждането на сферата в триизмерното пространство. Също така следвайки от Гаус, една сфера не може да бъде нанесена на равнина, като същевременно се поддържат както площи, така и ъгли. Следователно всяка картографска проекция въвежда някаква форма на изкривяване.
Сфера с радиус r има елементарна площ . Това може да се намери от обемния елемент в сферични координати като r се поддържа постоянно. [14]
Сфера с произволен радиус с център нула е интегрална повърхност със следната диференциална форма:
Това уравнение отразява, че позиционният вектор и допирателната равнина в дадена точка винаги са взаимно ортогонални. Освен това, обърнатият навън нормален вектор е равен на позиционния вектор, мащабиран с 1/r.
В римановата геометрия хипотезата за площта на запълване гласи, че полусферата е оптималното (най-малко площ) изометрично запълване на риманова окръжност.
Топология[редактиране | редактиране на кода]
Забележително е, че е възможно да се обърне обикновена сфера отвътре навън в тримерно пространство с възможни самопресичания, но без да се създават гънки, в процес, наречен обръщане на сферата.
Антиподният коефициент на сферата е повърхността, наречена реална проективна равнина, която също може да се разглежда като Северно полукълбо с идентифицирани антиподни точки на екватора.
Приложения[редактиране | редактиране на кода]
Хипотезата на Кеплер се отнася до подреждането на кълба с еднакъв радиус, така че да се увеличи максимално плътността на заемане на пространството.
Преносно значение[редактиране | редактиране на кода]
Думата „сфера“ се използва и в преносно значение, в смисъл на област на разпространение или развитие.
Източници[редактиране | редактиране на кода]
- ↑ * Мая Алашка, Райна Алашка, Пламен Паскалев. Математика 10 клас. България, Архимед, 2019. ISBN 978-954-779-278-4. с. 172. (на български)
- ↑ Taylor, Charles. An Introduction to the Ancient and Modern Geometry of Conics, page 196 („focal spheres“), pages 204 – 205 (history of discovery) (Deighton, Bell and co., 1881).
- ↑ Albert 2016, p. 60.
- ↑ В енциклопедията на Дидро и Д'Аламбер, например, сферата е „геометрично тяло, съдържащо се под една повърхност и което има в средата точка, която се нарича център, откъдето всички линии, начертани на повърхността, са равни.“ (s:L’Encyclopédie/1re édition/SPHERE) и има малка мнемонична рима за изчисляване на обема на сферата „Le volume de la sphère/est quoi qu'on puisse faire/quatre tiers de pi R trois/qu'elle soit en fer ou en bois“ – „Обемът на сферата/е каквото човек може да направи/четири трети от pi R на трета/независимо дали е от желязо или дърво“ (Roland Bouchot, L'Amour des mots, стр. 142)
- ↑ Eleven properties of the sphere // Geometry and the Imagination. 2nd. Chelsea, 1952. ISBN 978-0-8284-1087-8. с. 215 – 231.
- ↑ Albert 2016, p. 55.
- ↑ В математиката инвариантът е свойство на математически обект (или клас от математически обекти), което остава непроменено след прилагане на операции или трансформации от определен тип към обектите.
- ↑ а б Woods 1961, p. 266.
- ↑ Chisholm, Hugh, ed. (1911). „Sphere“. Енциклопедия Британика (11-о издание), Vol. 25. Cambridge University Press. pp. 647 – 648.
- ↑ Albert, Abraham Adrian – Solid Analytic Geometry, Dover, ISBN 978-0-486-81026-3, (2016) [1949].
- ↑ Steinhaus 1969, p. 223.
- ↑ The volume of a sphere – Math Central // Посетен на 2019-06-10.
- ↑ а б Collins Dictionary of Mathematics. 1989. ISBN 978-0-00-434347-1. с. 141, 149.
- ↑ а б в Sphere, Wolfram MathWorld.
- ↑ Steinhaus 1969, p. 221.
- ↑ Polyanin A. D., Manzhirov A. V. – Handbook of Mathematics for Engineers and Scientists, 69 стр. ISBN 9781584885023, издателство „Chapman & Hall/CRC“, 2007.
- ↑ Édouard Collignon – Traité de mécanique, volume 2, passage 296, éditeur „Hachette“, 1881.
- ↑ Mémoire de la Société royale des sciences de Liège, tome 6, passage 10, 1909.
































































![{\displaystyle A_{x}=(x_{1}^{2}+y_{1}^{2}+z_{1}^{2})[y_{2}(z_{3}-z_{4})+y_{3}(z_{4}-z_{2})+y_{4}(z_{2}-z_{3})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98aeceefde815d50b9c88071fd5af521cebcbd9b)
![{\displaystyle B_{x}=(x_{2}^{2}+y_{2}^{2}+z_{2}^{2})[y_{3}(z_{4}-z_{1})+y_{4}(z_{1}-z_{3})+y_{1}(z_{3}-z_{4})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e8fd51ac73a6f9738ad21bab83bc95106a37419)
![{\displaystyle C_{x}=(x_{3}^{2}+y_{3}^{2}+z_{3}^{2})[y_{4}(z_{1}-z_{2})+y_{1}(z_{2}-z_{4})+y_{2}(z_{4}-z_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8949e7118a516802283f47c40671877d166e202d)
![{\displaystyle D_{x}=(x_{4}^{2}+y_{4}^{2}+z_{4}^{2})[y_{1}(z_{2}-z_{3})+y_{2}(z_{3}-z_{1})+y_{3}(z_{1}-z_{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb66cc2d861cb44c430b1d4d444669e7d64ac50)
![{\displaystyle A_{y}=(x_{1}^{2}+y_{1}^{2}+z_{1}^{2})[z_{2}(x_{3}-x_{4})+z_{3}(x_{4}-x_{2})+z_{4}(x_{2}-x_{3})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0596cda990bc94b1c25e2dd59597025782fff0bc)
![{\displaystyle B_{y}=(x_{2}^{2}+y_{2}^{2}+z_{2}^{2})[z_{3}(x_{4}-x_{1})+z_{4}(x_{1}-x_{3})+z_{1}(x_{3}-x_{4})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7dda4bc308cb263a2b6fad07eee8b52afec515)
![{\displaystyle C_{y}=(x_{3}^{2}+y_{3}^{2}+z_{3}^{2})[z_{4}(x_{1}-x_{2})+z_{1}(x_{2}-x_{4})+z_{2}(x_{4}-x_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37e51cd29b0a770dbee0da4ecae0485674fb0147)
![{\displaystyle D_{y}=(x_{4}^{2}+y_{4}^{2}+z_{4}^{2})[z_{1}(x_{2}-x_{3})+z_{2}(x_{3}-x_{1})+z_{3}(x_{1}-x_{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75a4d722990be4e16b53049151c2c60670fe1f9a)
![{\displaystyle A_{z}=(x_{1}^{2}+y_{1}^{2}+z_{1}^{2})[x_{2}(y_{3}-y_{4})+x_{3}(y_{4}-y_{2})+x_{4}(y_{2}-y_{3})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36e18121f2b8cbbc0ba2a2471618f1595185f5dc)
![{\displaystyle B_{z}=(x_{2}^{2}+y_{2}^{2}+z_{2}^{2})[x_{3}(y_{4}-y_{1})+x_{4}(y_{1}-y_{3})+x_{1}(y_{3}-y_{4})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaf9dd4dead678b833a04a999c97feb8f9357d4b)
![{\displaystyle C_{z}=(x_{3}^{2}+y_{3}^{2}+z_{3}^{2})[x_{4}(y_{1}-y_{2})+x_{1}(y_{2}-y_{4})+x_{2}(y_{4}-y_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef5b67f4a5c22bce5874484e51f088679438eef3)
![{\displaystyle D_{z}=(x_{4}^{2}+y_{4}^{2}+z_{4}^{2})[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d904f3b36dc6b2cd7249cca7db350f3895ef61b6)















![{\displaystyle V=\pi \left[r^{2}x-{\frac {x^{3}}{3}}\right]_{-r}^{r}=\pi \left(r^{3}-{\frac {r^{3}}{3}}\right)-\pi \left(-r^{3}+{\frac {r^{3}}{3}}\right)={\frac {4}{3}}\pi r^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11b9db7c710d63e26e6870763b168617f643cf95)



















































