Меркаторова проекция

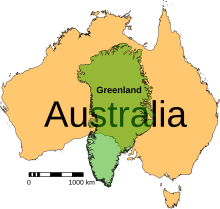
Меркаторовата проекция е цилиндрична картографска проекция, предложена от фламандския картограф Герардус Меркатор през 1569 г. Тя се превръща в стандартна картографска проекция за морски цели, заради способността си да представлява линии на постоянен курс, известни като локсодроми като прави сегменти, които държат ъглите с меридианите. Въпреки че линейната скала е равна във всички посоки около всяка точка, като по този начин запазва ъглите и формите на малки предмети, Меркаторовата проекция изкривява размера на предметите с увеличаване ширината от екватора до полюсите, където мащабът става безкраен. Така, например, земи като Гренландия и Антарктида изглеждат много по-големи, отколкото са в действителност по отношение на земни маси в близост до екватора, като Централна Африка.
Характеристики[редактиране | редактиране на кода]
- цилиндрична
- конформна
- паралелите са неравномерно разположени прави линии, сгъстени към екватора; секат меридианите под прав ъгъл
- меридианите са равномерно разположени прави линии
- мащабът е верен по дължината на екватора или при двата равноотдалечени от екватора стандартни паралела (при секантен вариант на проекцията)
- Локсодромите са прави линии
- Перспективата не се запазва
- Полюсите са в безкрайността; големи изкривявания на площите при полюсите
- употреба в навигацията
Проекцията обвива с цилиндър референтния елипсоид (земната сфера) и проектира земната повърхнина конформно (запазвайки ъглите) върху цилиндъра. Възможна е секантна вариация на проекцията при която цилиндъра не се допира до елипсоида, а го сече в два стандартни паралела.[1]
История[редактиране | редактиране на кода]

Проекцията е използвана за пръв път от Герардус Меркатор в картата му „Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendate Accommodata“ (Ново уголемено описание на Земята с корекции за навигационна употреба), издадена през 1569 г. Описанието на проекцията е дадено в каре, покриващо Северна Америка.[1]
Употреба[редактиране | редактиране на кода]
Както при всички картографски проекции, формата и големината са нарушения на реалното оформление на земната повърхност. Меркаторовата проекция увеличава земи, далеч от екватора. Например:
- Гренландия изглежда по-голяма от Африка, когато в действителност площта на Африка е 14 пъти по-голяма, а Гренландия е сравнима по площ с Алжир. Африка също изглежда приблизително същия размер като Европа, когато в действителност Африка е почти 3 пъти по-голяма.
- Аляска заема толкова площ на картата, колкото Бразилия, но площта на Бразилия е почти пет пъти по-голям от тази на Аляска.
- Финландия изглежда с по-голямо северюжно протежение от Индия, въпреки че Индия е по-голяма.
- Антарктида изглежда като най-големият континент (и би била безкрайно голяма на пълна карта), въпреки че тя всъщност е петият по големина континент.
Първата детайлна карта на чужда планета е издадена от USGS през 1972 г. в М1:25 000 000 и изобразява Марс в Меркаторова проекция.[1]
Трансформация[1][редактиране | редактиране на кода]
За сфероид[редактиране | редактиране на кода]
Координати от сферична геодезическа референтна система (датум) може да се трансформират към Декартови координати в Меркаторова проекция със следните формули:
-
(1.1)
-
(1.2)
или
-
(1.2a)
където
- – е радиусът на сферата
- – са дадени в радиани
Формули за в градуси:
-
(1.1a)
-
(1.2b)
За сфероид, обратна[редактиране | редактиране на кода]
Декартови координати в Меркаторова проекция към сферична геодезическа референтна система (датум) може да се трансформират със следните формули (в радиани):
-
(2.1)
или
-
(2.1a)
-
(2.2)
където
- – е Неперовото число
За елипсоид[редактиране | редактиране на кода]
-
(3.1)
-
(3.2)
или
-
(3.2a)
където
- – е екваториалния радиус на елипсоида
- – е неговия ексцентрицитет
За елипсоид, обратна[редактиране | редактиране на кода]
-
(4.1)
където
-
(4.2)
- – е Неперовото число
за начално се ползва
-
(4.3)
За изчисляването на ур. 4.1 се използва сходящ итеративен алгоритъм: Изчислява се по ур. 4.2. След това, използвайки начално от ур. 4.3 за дясната част на ур. 4.1, се изчислява вляво. Изчисленото се замества вдясно и калкулацията на ур. 4.1 се повтаря. Итеративният алгоритъм приключва когато изчисленото при текущата и предишната стъпка са еднакви.
-
(4.4)
Бележки[редактиране | редактиране на кода]
- ↑ а б в г Snyder, John. Map Projections:A Working Manual (USGS Professional Paper: 1395) // USGS, 1987.



![{\displaystyle y=\left(R/2\right)\left[\ln \left(\left(1+\sin \varphi \right)/\left(1-\sin \varphi \right)\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a550115ce7f1d0b3492fac63c44df5b52e91639)





![{\displaystyle \varphi =\arctan \left[\sinh \left(y/R\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b1a68e87b9d10e37dba08288b3e30104b12b30a)



![{\displaystyle y=a\ln \left[\tan \left(\pi /4+\varphi /2\right)\left({\frac {1-e\sin \varphi }{1+e\sin \varphi }}\right)^{\left(e/2\right)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a1439d851a8f183025f36c8e70629c6e9a205f2)
![{\displaystyle y=\left(a/2\right)\ln \left[\left({\frac {1+\sin \varphi }{1-\sin \varphi }}\right)\left({\frac {1-e\sin \varphi }{1+e\sin \varphi }}\right)^{e}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f73238a26b6157ad5a8794a5c2f17c09a64d7bf4)

![{\displaystyle \varphi =\pi /2-2\arctan \left\{t\left[\left(1-e\sin \varphi \right)/\left(1+e\sin \varphi \right)\right]^{\left(e/2\right)}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b55505e8bc919a4c5c10e97e361528843863da2)





