Площ

Площ (също и лице на повърхнина) е величина, изразяваща големината на даден двуизмерен обект.[1] Тя е двуизмерен аналог на едноизмерната дължина и триизмерния обем.
Площта на дадена фигура може да бъде определена, като се сравни с квадрат с предварително зададен размер. В Международната система единици площта се измерва в квадратни метри (m²) – площта на квадрат, чиито страни имат дължина 1 m.[2] Фигура с площ 3 квадратни метра би имала площта на три такива квадрата. В математиката площта е безразмерна величина, като за единица се използва единичният квадрат, квадрат с дължина на страните единица.
Площта на основните фигури, като триъгълници, правоъгълници и кръгове, обикновено се изчислява с помощта на няколко широко известни формули. Площта на произволен многоъгълник може да бъде определена чрез същите формули, като той бъде разделен на по-прости фигури, обикновено триъгълници.[3] За изчисляването на площта на по-сложни фигури с криволинейни граници обикновено са необходими методите на математическия анализ. В действителност задачата за определянето на площта на равнинни фигури е сред основните мотиви за първоначалното развитие на този дял на математиката.[4]
Площта на граничната повърхнина на триизмерни тела, като сфера, конус или цилиндър, се нарича околна повърхнина. Формули за околните повърхнини на прости тела са известни още от Античността, но изчисляването им за по-сложни обекти също се извършва с аналитични методи.
Площта играе важна роля в съвременната математика. Освен очевидната ѝ важност в геометрията и математическия анализ, тя е свързана с дефинирането на детерминантите в линейната алгебра, е една от основните характеристики на повърхнините в диференциалната геометрия.[5]
Единици за площ[редактиране | редактиране на кода]

Единицата за измерване на площ в системата SI е квадратният метър (с означение m2).
Някои по-често използвани производни единици на квадратния метър са квадратният километър, квадратният сантиметър, квадратният милиметър:
- 1 km2 = 1 000 000 m2
- 1 m2 = 10 000 cm2 = 1 000 000 mm2
Единицата ар (с означение а) и нейните кратни декар и хектар (с означения da и ha) се използват за измерване на селскостопански площи.
- 1 a = 100 m2
- 1 da = 10 a = 1000 m2
- 1 ha = 100 a = 10 000 m2
Постепенно излизат от употреба широко използваните в миналото (предимно в англоезичния свят) имперски единици (наричани още британски или английски):
- 1 in2 (квадратен инч) = 6,451 6 cm2
- 1 ft2 (квадратен фут) = 144 in2 = 929,03 cm2
- 1 yd2 (квадратен ярд) = 9 ft2 = 0,836 127 36 m2
- 1 rod2 (perch, pole) (квадратен род, пъч или пол) = 30,25 yd2 = 25,292 853 m2
- 1 acre (акър) = 160 rod2 = 43 560 ft2= 4046,856 m2
- 1 mile2 (квадратна миля) = 640 акра = 2,589 988 km2
Остарели руски единици са:
Основни формули за площ[редактиране | редактиране на кода]
Правоъгълници[редактиране | редактиране на кода]

Най-основната формула за площ (или лице на фигура) е тази за площ на правоъгълник. Ако дължината му е l и ширината w, формулата за площта е
- S = lw
С други думи, площта на правоъгълника е произведението на дължината и ширината му. Площта на квадрата е квадратът на страната му. Ако означим страната му с s тогава площта му е:
- S = s2
Тази формула служи за дефиниция или аксиома и произхожда от основните свойства на понятието площ. От друга страна, ако предположим, че геометрията идва преди аритметиката, тя може да послужи за дефиниция на произведението на две числа.

Повечето други формули се извеждат на базата на разделяне на всяка фигура на по-прости фигури, намиране на тяхната площ и събиране на отделните площи. Така например всеки успоредник може да се раздели на трапец и правоъгълен триъгълник. Ако триъгълникът бъде преместен от другата страна, се получава правоъгълник. Това показва, че лицето на успоредника се намира по аналогичен начин.
- S = bh
- където b е основата, а h височината.
Същият успоредник може да се раздели и на два еднакви триъгълника, по диагонала, като лицето на всеки един от тях е половината от лицето на успоредника:
Подобни аргументи могат да се ползват за да се намерят формули за лицето на ромб, трапец и други по-сложни фигури.
Лице на кръг[редактиране | редактиране на кода]

Формулата за лице на кръг се базира на подобен модел. Ако имаме кръг с радиус r, е възможно да се раздели на части, сектори, както е показано на фигурата. Всеки сектор е приблизително с формата на триъгълник и те могат да се пренаредят така, че да образуват успоредник (с добро приближение). Височината на успоредника е r, а основата е половината от обиколката на кръга или πr. По този начин лицето е r × πr или πr2:
- S = πr2
Въпреки че този път разделянето на отделни фигури е приблизително, грешката е много малка ако кръгът се раздели на все по-малки и по-малки триъгълници.
Този принцип всъщност е приложението на елементарните идеи на интегралното и диференциално смятане. Използвайки съвременни методи, лицето на кръга може да се намери от формулата:
Площ на плоска фигура[редактиране | редактиране на кода]
В декартови координати[редактиране | редактиране на кода]

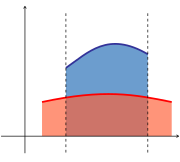
Площта, затворена между графиката на непрекъснатата функция в интервала и хоризонталната ос може да бъде изчислена като определения интеграл на следната функция:
Площта, затворена между графиките на непрекъснатите функции в интервала се намира като разликата от следните определените интеграли:
В полярни координати[редактиране | редактиране на кода]
В полярни координати: площта, ограничена от графиката на функцията и лъчите се изчислява по формулата:
- .
Лице на околна повърхнина[редактиране | редактиране на кода]
На конус[редактиране | редактиране на кода]
Лице на околната повърхнина на прав кръгов конус се нарича границата на редицата от лицата на околните повърхнини на вписаните в него (или описаните около него) правилни пирамиди при неограничено удвояване броя на околните им стени.
След съответните математически пресмятания и граничен преход се стига до формулите за лице на околна и пълна повърхнина:
- или
На цилиндър[редактиране | редактиране на кода]
Лицето на пълната повърхнина на прав цилиндър се дава от:
- 1,
а лицето само на околната повърхнина е
На пирамида[редактиране | редактиране на кода]
Лицето на околната повърхнина на правилна пирамида се намира по формулата:
където B е лицето на основата, P е периметърът на основата и L е:
където h е височината на пирамидата, а r е радиусът на вписаната окръжност.
На сфера[редактиране | редактиране на кода]
Повърхността на сфера не може да бъде направена плоска, както тази на цилиндър например, поради Гаусовата кривина. Формулата за първи път е изведена от Архимед.
- S = 4πr2
Където r е радиусът на сферата.
Бележки[редактиране | редактиране на кода]
- ↑ РБЕ
- ↑ Resolution 12 of the 11th meeting of the CGPM (1960) // bipm.org. BIPM, 2011. Посетен на 30 септември 2011. (на английски)
- ↑ De Berg, Mark et al. Computational Geometry. 2nd revised. Springer-Verlag, 2000. ISBN 3-540-65620-0. p. 45-61. (на английски)
- ↑ Boyer, Carl B. The History of the Calculus and Its Conceptual Development. Dover, 1959. ISBN 978-0486605098. (на английски)
- ↑ do Carmo, Manfredo. Differential Geometry of Curves and Surfaces. Prentice-Hall, 1976. p. 98. (на английски)



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)













