Делтаедър

Делтаедърът е многостен, чийто всички стени са равностранни триъгълници. Името му идва от гръцката буква Δ (делта), с която се означават равностранните триъгълници.

Изпъкнали делтаедри

Правилни делтаедри
Картинка	Име	Стени	Ръбове	Върхове	Връхни конфигурации	Група симетрия
	тетраедър	4	6	4	4 × 33	Td, [3,3]
	октаедър	8	12	6	6 × 34	Oh, [4,3]
	икосаедър	20	30	12	12 × 35	Ih, [5,3]
Джонсънови делтаедри
Картинка	Име	Стени	Ръбове	Върхове	Връхни конфигурации	Група симетрия
	триъгълна дипирамида	6	9	5	2 × 33 3 × 34	D3h, [3,2]
	петоъгълна дипирамида	10	15	7	5 × 34 2 × 35	D5h, [5,2]
	скосен дисфеноид	12	18	8	4 × 34 4 × 35	D2d, [2,2]
	триувеличена триъгълна призма	14	21	9	3 × 34 6 × 35	D3h, [3,2]
	квадратна завъртяноудължена дипирамида	16	24	10	2 × 34 8 × 35	D4d, [4,2]

Нестрого изпъкнали случаи

Съплоски делтаедри

Картинка	Име	Стени	Ръбове	Върхове	Връхни конфигурации	Група симетрия
	Увеличен осмостен Увеличение 1 tet + 1 oct	10	15	7	1 × 33 3 × 34 3 × 35 0 × 36	C3v, [3]
		4 3	12
	Триъгълен трапецоедър Увеличение 2 tets + 1 oct	12	18	8	2 × 33 0 × 34 6 × 35 0 × 36	C3v, [3]
		6	12
	Увеличение 2 tets + 1 oct	12	18	8	2 × 33 1 × 34 4 × 35 1 × 36	C2v, [2]
		2 2 2	11	7
	Триъгълен фрустум Увеличение 3 tets + 1 oct	14	21	9	3 × 33 0 × 34 3 × 35 3 × 36	C3v, [3]
		1 3 1	9	6
	Удължен осмостен Увеличение 2 tets + 2 octs	16	24	10	0 × 33 4 × 34 4 × 35 2 × 36	D2h, [2,2]
		4 4	12	6
	Тетраедър Увеличение 4 tets + 1 oct	16	24	10	4 × 33 0 × 34 0 × 35 6 × 36	Td, [3,3]
		4	6	4
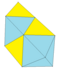
	Увеличение 3 tets + 2 octs	18	27	11	1 × 33 2 × 34 5 × 35 3 × 36	D2h, [2,2]
		2 1 2 2	14	9
	Ръбослят двадесетостен	18	27	11	0 × 33 2 × 34 8 × 35 1 × 36	C2v, [2]
		12 2	22	10
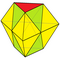
	Триъгълен бифрустум Увеличение 6 tets + 2 octs	20	30	12	0 × 33 3 × 34 6 × 35 3 × 36	D3h, [3,2]
		2 6	15	9
	Триъгълна купола Увеличение 4 tets + 3 octs	22	33	13	0 × 33 3 × 34 6 × 35 4 × 36	C3v, [3]
		3 3 1 1	15	9
	Триъгълна дипирамида Увеличение 8 tets + 2 octs	24	36	14	2 × 33 3 × 34 0 × 35 9 × 36	D3h, [3]
		6	9	5
	Шестоъгълна антипризма	24	36	14	0 × 33 0 × 34 12 × 35 2 × 36	D6d, [12,2+]
		12 2	24	12
	Пресечен тетраедър (Триангулиран пресечен тетраедър) Увеличение 6 tets + 4 octs	28	42	16	0 × 33 0 × 34 12 × 35 4 × 36	Td, [3,3]
		4 4	18	12
	Четириделен кубоктаедър Октаедър Увеличение 8 tets + 4 octs	32	24	18	0 × 33 12 × 34 0 × 35 6 × 36	Oh, [4,3]
		8	12	6

Звездовидни делтаедри

• Голям икосаедър
• Равностранен триделен тетраедър
• Равностранен четириделен хексаедър
• Равностранен триделен октаедър (звездовиден октаедър)
• Равностранен петоделен додекаедър
• Равностранен триделен икосаедър
• Изкопан додекаедър

Голям икосаедър (20 пресичащи се триъгълника)

Звездовиден октаедър (24 триъгълника)

Изкопан додекаедър (60 триъгълника)

Тороиден делтаедър (48 триъгълника)

Вижте също

• Тристен
• Делтоедър
• Триъгълник
• Триангулиран пресечен тетраедър