Побитова операция
Побитовата операция се прилага върху един бит или набор от повече отделни битове на двоични числа.[1] В компютрите всички данни и в частност числовите данни се представят като поредица от нули и единици. За целта се използва двоична бройна система. Например числото 55 в двоична бройна система се представя като 00110111.[1][notes 1]
Побитовата операция е много бърза, тъй като нейното изпълнение се осъществява пряко от микропроцесор с цел сравняване на различни стойности или прилагане на аритметични операции върху тях. На обикновен процесор за масова употреба побитовите операции са много по-бързи от събирането, изваждането, умножението и делението. По-новите процесори обикновено извършват умножение и събиране не по-бавно отколкото побитови операции. Това се дължи на техните по-дълги конвейери (instruction pipelines) за инструкции и архитектурен дизайн. В общия случай побитовите операции използват по-малко ресурси.
Побитови оператори[редактиране | редактиране на кода]
Оператор за побитово отрицание (NOT)[редактиране | редактиране на кода]
Операторът побитово отрицание (bitwise NOT), наричан също допълнение, е унитарна операция (операция с един операнд) която извършва логическо отрицание за всеки бит. Така се сформира допълнението за дадената двоична стойност. Битовете, които са били със стойност 0, приемат стойност 1, а битовете със стойност 1 стават 0. Например:
NOT 1010 (десетично 10) = 0101 (десетично 5)
Побитовото допълнение е равно на допълнението на две на дадена стойност, минус едно. Ако се използва аритметично допълнение на две, тогава:
NOT x = -x -1
За беззнакови целочислени типове (unsigned integers), побитовото допълнение на число е „огледалният образ“ на числото, намиращо се по средата на обхвата на беззнаковия целочислен тип. Например при 8 битовите беззнакови целочислени типове, NOT x = 255-x, може да бъде визуализирано на графика като намаляваща линия, която преминава в нарастваща, от 0 до 255, след което отново започва да намалява, преминавайки в диапазона от 255 до 0. Един прост, но доста описателен пример, е обръщането на черно-бели изображения, където всеки един пиксел се съхранява като беззнаков целочислен тип.
Обикновено побитовото отрицание се записва със знак „~“. В таблицата по-долу се вижда как работи побитовото отрицание върху бит А.[2]
| А | NOT |
|---|---|
| 0 | 1 |
| 1 | 0 |
И (AND)[редактиране | редактиране на кода]
Побитовото И (AND) използва две двоични числа с еднаква дължина и прави логическо И на всяка двойка съответстващи битове. Резултатът на дадена позиция е 1, ако първият бит е 1 и вторият е 1, в противен случай резултатът е 0. Използваме умножение на битовете : 1 × 0 = 0 и 1 × 1 = 1. Например:
0101 (десетично 5) AND 0011 (десетично 3) = 0001 (десетично 1)
Този оператор може да се използва, за да определим дали даден бит е вдигнат (има стойност 1), или е свален (има стойност 0). Например, ако искаме за дадена поредица от битове 0110 (десетично 6), да разберем състоянието на втория бит, може да използваме оператор побитово „И“ за гореспоменатата поредица и поредица, където само втория бит е 1:
0110 (десетично 6) AND 0010 (десетично 2) = 0010 (десетично 2)
Понеже резултатът 0010 не е нула, знаем че вторият бит в оригинала е бил вдигнат. Това често бива наричано битово маскиране.(Аналогично на това как бояджийското тиксо покрива/маскира местата, които не трябва да бъдат да бъдат променяни или не представляват интерес. В този случай нулите маскират битовете, които не ни интересуват.) Ако запазим резултата, това свойство може да се използва, за да се свалят избрани битове.
Ако вземем за пример 0111 (десетично 7), вторият бит може да бъде свален, използвайки побитово „И“, заедно с поредица от битове, която има 0 само на втора позиция:
0111 (десетично 7)
AND 1101 (десетично 13)
= 0101 (десетично 5)
За побитово „И“ се използва знак „&“. В долната таблица е описано действието на тази операция върху битовете А и В: [2]
| A | B | AND |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
ИЛИ (OR)[редактиране | редактиране на кода]
Побитовото ИЛИ взима две числа с еднаква дължина и прави логическа дизюнкция ИЛИ на всяка двойка съответстващи битове. Резултатът на дадена позиция е 1, ако първият или вторият бит има стойност 1 или ако и двата бита са равни на едно. В противен случай резултатът е 0. Например:
0101 (десетично 5) OR 0011 (десетично 3) = 0111 (десетично 7)
Побитово „ИЛИ“ може да се използва за задаване на стойност 1 на определени битове, например ако имаме специфичен бит (флаг) от регистър, където всеки бит представлява единична булева стойност. Например 0010 (2 десетично) се състои от четири флага като първият, третият и четвъртият флаг имат стойност 0, а вторият има стойност 1. Чрез побитово „ИЛИ“ може да се зададе стойност 1 на четвъртия бит :
0010 (десетично 2) OR 1000 (десетично 8) = 1010 (десетично 10)
Тази техника е много ефективен начин за съхраняване на булеви стойности, използвайки възможно най-малко памет.
Побитовото „ИЛИ“ се означава със знак „|“. В таблицата долу е представена функцията на оператора върху битове А и В. [2]
| A | B | OR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Изключващо ИЛИ (XOR)[редактиране | редактиране на кода]
Изключващото ИЛИ (XOR) взима две числа с еднаква дължина и прави логическо изключващо ИЛИ на всяка двойка съответстващи битове. Резултатът е равен на 1, ако само първият бит е 1 или ако само вторият бит е 1, но ако и двата бита са равни на 1 или и ако и двата бита са равни на 0, резултатът е 0. В следващия пример се прави сравнение между два бита и резултатът е 1, ако двата бита са различни и 0, ако са еднакви :
0101 (десетично 5) XOR 0011 (десетично 3) = 0110 (десетично 6)
Изключващото „ИЛИ“ може да се използва за обръщане на битове (също така наричано toogle или flip. Всеки бит може да са обърне след XOR с 1. Например в числото 0010 (2 десетично) може да обърнем втория и четвъртия бит след изключващо ИЛИ с число, чиито битове на позиция две и четири имат стойност 1.
0010 (десетично 2) XOR 1010 (десетично 10) = 1000 (десетично 8)
Програмистите на асемблер често използват XOR като по-лесен начин да променят стойността на някой регистър на нула. Ако се направи изключващо „ИЛИ“ на две еднакви числа, резултатът е 0. В повечето архитектури тази операция изисква много по-малко цикли и/или памет, отколкото задаването на нулева стойност и запазването ѝ в регистъра.
Таблицата на побитовото изключващо „ИЛИ“ за битове А и В изглежда по следния начин: [2]
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Побитови измествания (Bit shifts)[редактиране | редактиране на кода]
Побитовите измествания често се смятат за побитови операции, понеже те работят с двоичното представяне на цяло число, а не с числовата му стойност. Побитовите измествания не са същински побитови операции, понеже не действат върху отделни битове или двойки от такива. В този тип операции цифрите в двоичния запис се изместват съответно наляво или надясно. Регистрите в компютрите имат фиксирана дължина. Вследствие на това някои битове от единия край ще бъдат „изместени извън“ регистъра, докато от другия ще бъдат „изместени навътре“ същият брой битове. Разликата във видовете побитовите измествания, се състои в това какви битове се изместват в регистъра.
Аритметично изместване (Arithmetic shift)[редактиране | редактиране на кода]

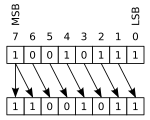
При аритметичното изместване стойностите на битовете, изместени навън, не са от значение. При изместване наляво от дясната страна се добавят нули. При изместване надясно от ляво се добавя най-старшият бит. Този бит указва знака и поради това знакът на числото остава непроменен. При изместване надясно с повече от една позиция, копия на старшия бит се изместват навътре. Това значи, че при изместване надясно с N позиции върху число със старши бит 1, съответните N позиции ще се запълнят с 1.
Следващият пример използва 8-битов регистър:
00001100 (десетично +12) Изместване-наляво = 00011000 (десетично +24)
10010111 (десетично -105) Изместване-надясно = 11001011 (десетично -53)
В първия случай най-левият бит се измества навън и от дясната страна се добавя нова 0 на най-дясна позиция. Във втория пример най-десният бит със стойност 1 се измества извън регистъра. Понеже старшият бит преди операцията е 1, то от лявата страна навътре се измества 1, запазвайки знака на числото. Няколко измествания в една посока може да бъдат записани като едно, като бъде указано колко пъти да е приложено. Това позволява по-къс запис. Например:
00011010 (десетично +26) Изместване-наляво-с-две = 01101000 (десетично 104)
Прилагането на ляво аритметично изместване N пъти е еквивалентно на умножение с 2N (ако числото не „прелее“ и значими битове не бъдат изхвърлени извън регистъра). Изместване надясно с N позиции за стойност записана по метода на „допълнение на две“ (two's complement) е еквивалентно на деление с 2N при закръгляне към минус безкрайност. При стойност, записана като „допълнение на едно“ (one's complement), същата операция би довела до делене с 2N и закръгляне към 0.
Логическо изместване[редактиране | редактиране на кода]
 |
 |
При логическото изместване битовете изместени навън се заместват с нули. Това прави логическото изместване еднакво с аритметичното изместване наляво.
При изместването надясно, от най-дясната страна се вкарват нули. Това прави логическото изместване подходящо за работа с цели числа без знак, докато аритметичното е подходящо за такива със знак.
Завъртане без пренасяне[редактиране | редактиране на кода]
 |
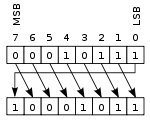 |
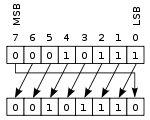
Друг вид изместване е кръгово изместване или завъртане на битове. При този вид изместване битовете се „завъртат“. Стойността, която се вкарва в десния край при изместване наляво, е тази, която бива изместена навън от лявата част. Това изместване е полезно, ако е нужно да се запазят съществуващите битове. Това свойство често се използва в дигиталната криптография.
Завъртане с пренасяне[редактиране | редактиране на кода]
 |
 |
Завъртането с пренасяне е подобно на операцията „завъртане без пренасяне“. За разлика от „завъртане без пренасяне“, при завъртането с пренасяне двете страни на регистъра са „разделени“ с пренасящ флаг.
Битът, който се вкарва в регистъра при изместване (в коя да е страна), е старата стойност на флага, а битът, който е напуснал регистъра, става новата стойност на флага.
Единично завъртане с пренасяне може да симулира логическо или аритметично изместване с една позиция, поставяйки предварително стойност на пренасящия флаг. Поради това някои микроконтролери поддържат само завъртащите измествания и не поддържат аритметично или логическо изместване.
Изместването с пренасяне е крайно полезно при измествания на числа по-големи от процесорна дума. Така, когато номер се съхранява в повече от един регистър, битът който излезе от десния край на първия регистър трябва да се постави в левия край на втория. При изместването с пренасяне, битът е „запазен“ в пренасящия флаг при първото изместване, готов да бъде вмъкнат при изместването на втория регистър без допълнителни приготовления.
Изместване в C, C++ и C#[редактиране | редактиране на кода]
В езиците наследници на C, операторите за ляво и дясно побитово изместване са съответно „<<“ и ">>".
Номерът на позициите на изместването се задава като втори операнд. Пример:
x = y << 2;
Примерът ще присвои на x стойността на y, изместена с 2 позиции наляво.
В C и C++, при изчисления с ляв операнд от целочислен тип без знак се използва логическо изместване. В C# изместването надясно е аритметично, ако първият операнд е целочислен тип със знак. Ако първият операнд е от целочислен тип без знак, се използва логическо изместване. Побитовото изместване в C, за ляв операнд цяло число със знак, има като резултат в общия случай:
- За"
<<": y×2(брои изместени полета) (недефинирано, ако извън регистъра се изместят значими битове); - За „
>>“: зависи от имплементацията (най-често резултатът е: y/2(брой изместени полета) (закръгляне към отрицателна безкрайност).
Изместване в Java[редактиране | редактиране на кода]
В Java всички целочислени типове са със знак и операторите „<<“ и ">>" извършват аритметично изместване. В Java има добавен оператор „>>>>“ за прилагане на логическо изместване наляво. Понеже логическото и аритметичното изместване се държат еднакво при изместване надясно, не съществува оператор „<<<<“ в Java.
Допълнителни детайли за изместванията в Java:
- Типът, връщан от изместването, е типът на левия операнд.
- Когато левият операнд е от тип int, само най-ниските шест бита на десния операнд се взимат под внимание. Същото би се получило, ако се използва побитово „И“ върху десния оператор заедно е маска 111111 (десетично 31). Така стойността на десния операнд винаги е между 0 и 31 включително.
- Когато левият операнд е от тип long, само най-ниските пет на десния операнд се взимат под внимание. Същото би се получило ако се използва побитово „И“ върху десния операнд заедно с маска 1111111 (десетично 63). Така стойността на десния операнд винаги е между 0 и 63 включително.
Измествания в Pascal[редактиране | редактиране на кода]
В езика Pascal, както и във всички негови диалекти, левият и десният оператор за изместване са съответно, „shl“ и „shr“. Номерът на изместените позиции е вторият аргумент. В следния пример x приема стойност y, изместен с 2 бита наляво:
x := y shl 2;
Приложения[редактиране | редактиране на кода]
Побитовите операции са особено нужни за програмирането на ниско ниво (като например писане на драйвери за устройства, графики на ниско ниво, конструкция на пакети за протоколи за комуникация и декодиране).
Въпреки че машините често имат вградени ефективно работещи инструкции за изпълнение на аритметични и логически операции, всъщност всички те могат да се извършат чрез комбинация на побитови операции и „zero-testing“ по различни начини.
Ето примерен псевдокод, който показва как се умножават две произволни числа от целочислен типa и b (a по-голямо b) с използване само на побитови измествания и събиране.
c = 0
while b ≠ 0
if (b and 1) ≠ 0
c = c + a
left shift a by 1
right shift b by 1
return c
NB: В настоящия пример = е оператор за присвояване на стойност на променлива, а не оператор за равенство.
Следната имплементация на древноегипетското умножение като повечето алгоритми за умножение, използва побитови измествания. Дори събирането може да бъде изразено единствено чрез побитови измествания.
while a ≠ 0
c = b and a
b = b xor a
left shift c by 1
a = c
return b
NB: В настоящия пример = е оператор за присвояване на стойност на променлива, а не оператор за равенство.
Бележки[редактиране | редактиране на кода]
- ↑ В примерите по-долу позициите на битовете се броят от дясно наляво. Например двоичната стойност 0001 (еквивалентна на 1 в десетичен запис) има нули на всички позиции с изключение на първата.
Вижте също[редактиране | редактиране на кода]
Източници[редактиране | редактиране на кода]
- ↑ а б „Въведение в програмирането със C#“, Светлин Наков, Изд. „Фабер“, Велико Търново, 2011, ISBN 978-954-400-527-6
- ↑ а б в г д е ж з learn.fmi.uni-sofia.bg[неработеща препратка] изисква регистрация
