Матрица (математика)
- Вижте пояснителната страница за други значения на матрица.
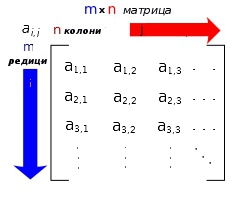
Матриците са основен елемент от линейната алгебра. В математиката, матрица представлява правоъгълна таблица от величини, най-често числа (числова матрица), наричани елементи на матрицата. Елементи на матрица могат да са числа, вектори, функции или други математически обекти.[1] Те могат да бъдат от произволно поле (например или ) или пръстен. Матриците и матричната алгебра са основни в линейната алгебра. Те се използват за решаване на линейни системи, линейни преобразувания и собствени стойности.[2] Матрица от тип m × n над поле F се нарича матрица, елементите на която са от полето F и има m реда и n стълба:
Множеството от матриците над поле F от тип m × n им може да се запише като Fmxn.
Пример за матрица 4 × 3 над полето на реалните числа:
Математическа нотация[редактиране | редактиране на кода]
Обикновено матриците се отбелязват с главни латински букви – например A, а елементите на матрицата се записват със съответната малка или главна буква – aik или Aik, като първият индекс показва номера на реда, а вторият – номера на стълба, на който се намира елементът в матрицата. Освен скоби от вида [ ], е възможно изписване с ( ) и
Елементи на матриците[редактиране | редактиране на кода]
В една квадратна матрица от ред n, елементите с равни индекси (aii, i=1.. n) образуват главния ѝ диагонал:
Елементите, сборът от индексите на които е равен на n+1 (aij, i=1.. n, j=n..1), образуват страничния диагонал:
Видове матрици[редактиране | редактиране на кода]
Най-често се използват матрици с елементи от полето и . В първия случай матрицата се нарича реална, а във втория – комплексна.
- нулева матрица (0) – матрица, при която всички елементи са нули:
- квадратна матрица – матрица с равен брой на редове и колони:
- правоъгълна матрица – матрица с различен брой редове и колони:
- триъгълна матрица – квадратна матрица, при която елементите под или над главния диагонал са нули, съответно горна или долна триъгълна матрица:
- диагонална матрица – квадратна матрица, чиито елементи, неучастващи в главния диагонал, са нули:
- скаларна матрица – диагонална матрица, елементите от главния диагонал на която са равни:
- единична матрица (E) – скаларна матрица с елементи от главния диагонал равни на единица:
- еднакви матрици – когато , тоест съответните им елементи са равни.[1]
- симетрична матрица – квадратна матрица , за която е изпълнено :
- антисиметрична матрица – квадратна матрица , за която е изпълнено :
Елементарни преобразувания с матрици[редактиране | редактиране на кода]
- смяна на местата на два реда:
- прибявяне на един ред на матрица към друг:
- умножаване на ред на матрицата с число различно от 0:
Основни операции с матрици[редактиране | редактиране на кода]
Транспониране[редактиране | редактиране на кода]
- Транспонирането е унарна операция. Транспонирата матрица се бележи с AT и се получава, като в матрицата A редовете се запишат като стълбовете, т.е. аTij = аji. Пример:
Събиране[редактиране | редактиране на кода]
- Събират се само матрици от един и същи ред.[1] Елементите на новополучената матрица (сбора), са равни на сбора на съответните елементи от събираните матрици:
Свойства:[1]
- комутативност:
- асоциативност:
- дистрибутивност: ,
- неутралност на нулевата матрица:
- , където A и B са еднакви матрици
- противоположната матрица на матрицата А означаваме с –А, за която е в сила
- разликата на матриците А и В е матрицата , като към А прибавим противоположната матрица на В, тоест :
Умножение на матрица с число (скалар)[редактиране | редактиране на кода]
- Всеки елемент на матрицата се умножава с числото:[1]
Свойства:
- ако , то
- ако А и В са еднакви матрици, то
Умножение на матрици[редактиране | редактиране на кода]
- Умножението на матриците A и B е дефинирано само когато A е съгласувана с B, т.е., когато броят на стълбовете на A е равен на броя на редовете на B. Произведението Cm x p на Am x n и Bn x p се дефинира с равенството:
Тоест всеки ред на матрицата A се умножава последователно с всеки от стълбовете на B, като всяко от тези произведения дава един елемент от реда на матрицата C с номер, съвпадащ с този на A. Първият ред на A, умножен с всички стълбове на B, дава всички елементи от първия ред на C и т.н. Пример:
Свойства:
- две квадратни матрици могат да бъдат умножени само ако са от един и същи ред
- комуникативност – не е в сила за произволни матрици
- асоциативност:
- дистрибутивност:
Ранг[редактиране | редактиране на кода]
При дадена произволна матрица с размерност можем да разгледаме нейните редове като n-мерни вектори:
,
а колоните ѝ – като m-мерни вектори:
, .
Размерността на подпространоството (в повечето случаи подпоространство на или ) се нарича хоризонтален, или ред-ранг на матрицата , а размерността на подпространостното – вертикален, или стълб-ранг на матрицата.[3]
Детерминанта[редактиране | редактиране на кода]
Детерминантата е свойство на всяка квадратна матрица, при което тя може да се съпостави на едно число |A|:
,
където сумата е по всички пермутации (k1k2 … kn) на числата 1,2,…,n и I е броят на инверсиите в съответната пермутация. Инверсия в пермутация – , при .
В сила е нотацията .
Ако детерминантата на матрицата е различна от 0 (редовете ѝ са линейно независими), матрицата е линейно преобразувание. Нейно харктеристично уравнение е
Пресмятане на детерминанта[редактиране | редактиране на кода]
За детерминанта от първи ред:
За детерминанта от втори ред:
За детерминанта от трети ред:
В останалите случаи, най-често свеждаме матрицата до горно или долно триъгълна чрез елементарни преобразувания (умножение на ред или стълб с дадено число и прибавяне на реда към друг ред (или прибавяне на стълб към друг стълб)).
Детерминанта от n-ти ред се пресмята чрез развитие по ред или по стълб – една матрица от n-ти ред се получават n детерминати от (n-1)-ви ред.
Източници[редактиране | редактиране на кода]
- ↑ а б в г д Латка, Франтишек. Минисправочник по математика. София, Регалия 6, 1992. ISBN 954-8147-02-5. с. 36 – 42.
- ↑ Каменаров, Георги. Справочник Висша математика. София, Техника, 1994. ISBN 954-03-0352-4. с. 65 – 104.
- ↑ Тонов, Иван. Матрици и детелминанти. София, Народна просвета, 1980. с. 54 – 69.
Външни препратки[редактиране | редактиране на кода]
 В Общомедия има медийни файлове относно Матрица (математика)
В Общомедия има медийни файлове относно Матрица (математика)- ((en)) Статия „Матрица“ в Wolfram MathWorld


































































![{\displaystyle {\mathsf {|A|}}=det[A]=\Delta _{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68ba5427a2bb99f27117dbb3228f17d95f380571)




