Корелация
Корелация е математически термин, с който в общ смисъл се означава мярка за стохастична (вероятностна, нефункционална) зависимост между случайни величини и означава статистическа взаимна връзка между две или повече случайни величини. [1]
Високата корелация между две величини не предполага задължително наличие на причинно-следствена връзка между тях. Например измерванията в група градове на процента шофьори и средното ниво на продажба на алкохол могат да разкрият високи нива на корелация между двете величини, но това е отражение на броя на жителите във всеки град върху всяка от двете измервани величини.
В по-тесен смисъл терминът корелация се разбира като синоним на корелационен коефициент ρ, който представлява мярка за зависимост между две случайни величини и , дефинирана като тяхната ковариация, нормирана с (разделена на) произведението на средноквадратичните им отклонения (вариации): [1]
- .
Ако случайните величини са независими, те са некорелирани, т.е. . От друга страна тогава, когато изследваните случайни величини са свързани с линейна зависимост. [2]
- Пример:

Показатели за корелация[редактиране | редактиране на кода]
Показатели за корелация могат да се разделят на две групи: параметрични и непараметрични. [3]
Параметрични показатели за корелация[редактиране | редактиране на кода]
- Ковариация (корелационен момент) [2] където с е обоначено математическото очакване (в англоезичната литература е прието обозначението от expected value).

- Коефициент на линейна корелация или [3]
Непараметрични показатели за корелация[редактиране | редактиране на кода]
- Коефициент на рангова корелация на Кендъл
- Коефициент на рангова корелация на Спирмeн
- Коефициент на знакова корелация на Фехнер
- Коефициент на множествена корелация
- Коефициент на множествена рангова корелация (съгласуваност)
Корелационен анализ[редактиране | редактиране на кода]
Корелационният анализ е метод за обработка на статистически данни, използвани за изучаване на корелации между променливи величини. При анализа се сравняват коефициентите на корелацията между една или повече двойки променливи, за да се установят статистически взаимозависимости между тях.
Статистическите процедури, с които се определя степента на взаимозависимост, се отнасят до категорията на корелационния анализ. Корелационен индекс е степента, в която две променливи са взаимно свързани. Целта на корелационния модел е да идентифицира степента на свързаност между два феномена. Ако целта на изследването е фокусирана върху предсказване на дадена променлива, основано на информация от друга променлива, тогава се прилага регресионен метод. Регресионният модел показва промените в една променлива като функция от промени или различия на фиксирани стойности на други променливи. Корелационният анализ може да се прилага, когато има събрани данни в две различни променливи. Условно едната променлива е X, а другата Y. За X и Y за всяко изследвано лице трябва да има стойности. Корелационния анализ представлява бивариационно честотно разпределение. Обикновено с X се означава независимата променлива (фактора), а с Y – зависимата променлива (резултата).
Най-широко използваният индекс за праволинейна зависимост се нарича коефициент на линейна корелация или коефициент на корелация на Пирсон – единичен, резюмиран индекс на степента, в която две променливи са линейно свързани или зависими една от друга. Стандартният символ, с който се бележи коефициентът на корелация е R (или r). Има стойност от (–1) до 1. Когато R=0, няма линейна връзка между променливите, т.е няма никаква корелация. Когато R=1 или R= –1, имаме перфектна линейна връзка между двете променливи. Това означава, че диаграмата в тези случаи ще бъде права линия. Знакът пред R показва посоката на зависимостта между двете променливи. Когато R е с положителен знак има права зависимост между двете променливи – при нарастване на X, нараства и Y. Когато знакът е отрицателен, има обратна зависимост – с нарастване на X, намалява Y. Изчислява се по формулата:
където и са средни стойности на величините от на брой измервания (извадки). [2][3]
Този коефициент на корелация зависи от целта на изследването. Трябва да се интерпретира съдържателно. Интерпретацията не може да бъде еднаква за резултати от рода на 0,3 и 0,7. Корелационната скала е ординална, а не интервална. Има две мнения в науката относно тълкуването на коефициента:
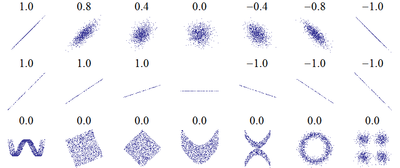
0 < R < 0,3 – слаба корелация
0,3 < R < 0,5 – умерена корелация
0,5 < R < 0,7 – значителна корелация
0,7 < R < 0,9 – висока корелация
0,9 < R < 1 – много висока корелация
Другата скала за R е:
0 – 0,2 – слаба корелация
0,2 – 0,4 – умерена корелация
0,4 – 0,6 – значителна корелация
0,6 – 0,8 – висока корелация
0,8 – 1 – много висока корелация
Коефициентът на корелация R e по-лесен за работа, когато е повдигнат на квадрат R2, с което се получава параметърът коефициент на определеност. Така може да се представи зависимостта между двете променливи като процент от вариации между тях. Примери: R=0,5 и R=0,9. Коефициентите на определеност са R2=(0,5)2 x100=25% и R2=(0,9)2 x100=81%. Това означа, че съответно 25% и 81% от промените в резултативната променлива Y са в резултат от измененията на факторната променлива X. [1]
Коефициентът на определеност се нарича още коефициент на детерминация и показва какъв процент от промените във факторната променлива ще доведат до промени в резултативната променлива. Коефициентът на детерминация и коефициентът на неопределеност К2 се допълват до единица (100%). Ако R2=25% => K2=75%. [1]
При интерпретация на корелационния анализ сe описва посоката на връзката – дали е положителна или отрицателна, дали има права или обратна зависимост. Това означава, че ако има положителен знак, повишаването на стойността на едната променлива ще доведе до повишаване на стойността на другата, както и обратното. Когато знакът е отрицателен, повишаването на стойността на едната променлива води до понижаване на стойността на другата, както и обратното.
Източници[редактиране | редактиране на кода]
- ↑ а б в г Общая теория статистики: Учебник / Под ред. Р. А. Шмойловой. — 3-е издание, переработанное. — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8.
- ↑ а б в Гмурман В. Е.ruuk. Теория вероятностей и математическая статистика: Учебное пособие для вузов. — 10-е издание, стереотипное. — Москва: Высшая школа, 2004. — 479 с. — ISBN 5-06-004214-6.
- ↑ а б в Елисеева И. И., Юзбашев М. М. – Общая теория статистики: Учебник / Под ред. И. И. Елисеевой. — 4-е издание, переработанное и дополненное. — Москва: Финансы и Статистика, 2002. — 480 с. — ISBN 5-279-01956-9.






![{\displaystyle \mathrm {cov} _{XY}=\mathbf {M} \left[(X-\mathbf {M} (X))(Y-\mathbf {M} (Y))\right]=\mathbf {M} (XY)-\mathbf {M} (X)\mathbf {M} (Y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c5c50d8f681d17ae291067e2ce2ae04967222ee)













