Теорема и вектор на Пойнтинг

Излъчване от дипол, показващо силата на електричното поле (цвят) и вектора на Пойнтинг (стрелки) в равнината.

Теорема на Пойнтинг или уравнение на Пойнтинг представлява енергийното уравнение на електродинамиката, описващо закона за запазване на енергията на електромагнитното поле. Уравнението има следната обща диференциална форма:

${\mbox{div}}\,{\vec {\Pi }}=-{\frac {\partial }{\partial t}}\left[{\frac {1}{2}}({\vec {E}}\cdot {\vec {D}}-{\vec {B}}\cdot {\vec {H}})\right]-{\vec {E}}(t,{\vec {r}})\cdot {\vec {j}}(t,{\vec {r}})$,

където ${\vec {E}}$ и ${\vec {H}}$ са съответно интензитетите на електрическото и магнитното полета; ${\vec {D}}$ е векторът на елекрическото сместване (електрическа индукция), а ${\vec {B}}$ – векторът на магнитната индукция; векторната величина ${\vec {\Pi }}={\vec {E}}\times {\vec {H}}$ се нарича вектор на Умов – Пойнтинг или вектор на Пойнтинг; ${\vec {j}}$ е плътността на тока.

Общата концепция за потока на механична енергия в пространството е въведена за първи път от Николай Алексеевич Умов (1846 – 1915) през 1874 г. за еластични среди и вискозни флуиди. На тази основа в по-стари публикации векторът на плътността на енергийния поток от всякакъв физически характер се нарича вектор на Умов. През 1884 г. Джон Пойнтинг развива концепции за плътността на електромагнитния енергиен поток. Затова векторът на плътността на потока електромагнитна енергия се нарича вектор на Умов – Пойнтинг или за краткост вектор на Пойнтинг. Той изразява плътността на потока на електромагнитната енергия за единица време (с размерност $W/m^{2}$) и има посока, съвпадаща с посоката на разпространение на енергията на полето. Означава се с ${\vec {\Pi }}$, ${\vec {S}}$, ${\vec {R}}$ или ${\vec {N}}$.

През 1884 година Джон Хенри Пойнтинг (1852 – 1914) публикува теоремата в статията За пренасянето на енергия в електромагнитното поле в издание на кралското научно общество в Лондон . Пойнтинг също предприема обширни експерименти за определяне на гравитационната константа.

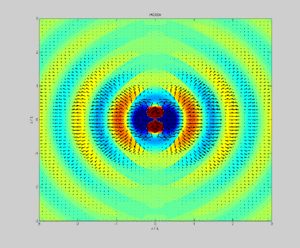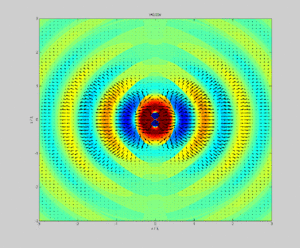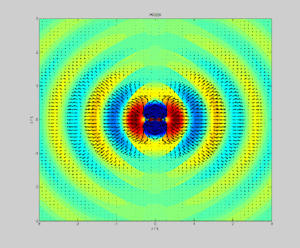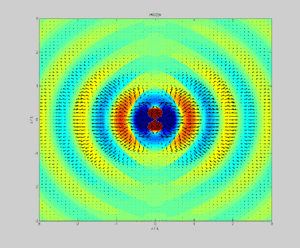
Първият израз от дясната страна на уравнението показва степента на намаляване във времето на потенциалната или запасената енергия в разглежданата система. Изразът има две компоненти: едната е степента на промяна във времето на енергията на електрическото поле, а другата степента на промяна на запасената енергията на магнитното поле. Вторият израз в дясната част на уравнението съответства на източници на енергия, които могат да съществуват в разглеждания обем (токова плътност, породена от батерия или генератор в обема) или токова плътност, предизвикана от външни източници (индукционни токове). Трябва да се обърне внимание, че изразът ${\vec {E}}(t,{\vec {r}})\cdot {\vec {j}}(t,{\vec {r}})$ е положителен, когато съответства на източник в обема, и отрицателен при енергия, доставена от външен източник.

В интегрална форма уравнението на Пойнтинг се записва като:

$\oint _{(s)}{\vec {S}}{\vec {ds}}=-{\frac {\partial }{\partial t}}\int _{(V)}\left[{\frac {\epsilon E^{2}}{2}}+{\frac {\mu H^{2}}{2}}\right]dv-\int _{(V)}{\vec {E}}\cdot {\vec {j}}dv$,

Уравнението се получава, използвайки изразите ${\vec {D}}=\epsilon {\vec {E}}$ (${\vec {D}}$ е векторът на електрическата индукция или плътността на електрическия поток) и ${\vec {B}}=\mu {\vec {H}}$ (${\vec {B}}$ е векторът на магнитната индукция или плътността на магнитния поток), $\epsilon$ е диелектричната проницаемост и $\mu$ е магнитната проницаемост на средата. В този си вид уравнението изразява баланс на мощности, измервани във VA (за реактивната) и W (за активната мощност).

Векторът на Пойнтинг при електростатично поле е равен на нула. При такова поле няма електромагнитно излъчване.

Източници

• Сава П. Папазов, Самуил Л. Фархи. Теоретична електротехника, част 3. Държавно издателство Техника, 1988.
• Nathan Ida. Engineering Electromagnetics. Springer, 2004.
• S. Brandt, H.D. Dahmen. Elektrodynamik. Springer, 2005.