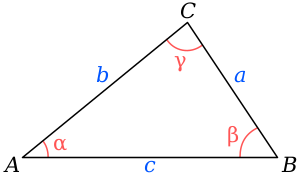
Косинусовата теорема в геометрията гласи:
Квадратът на коя да е страна в триъгълник е равен на сбора от квадратите на другите две страни минус удвоеното произведение на тези две страни и косинуса на ъгъла, заключен между тях.
Разглежда се триъгълник
A
B
C
{\displaystyle ABC}
A
B
=
c
{\displaystyle AB=c}
B
C
=
a
{\displaystyle BC=a}
C
A
=
b
{\displaystyle CA=b}
Фиг. 1 . Косинусова теорема.Тогава е в сила равенството
c
2
=
a
2
+
b
2
−
2
a
b
cos
γ
{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos \,\gamma }
Тук, с
γ
{\displaystyle \gamma }
a
{\displaystyle a}
b
{\displaystyle b}
b
{\displaystyle b}
c
{\displaystyle c}
a
2
=
b
2
+
c
2
−
2
b
c
cos
α
{\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \,\alpha }
b
2
=
a
2
+
c
2
−
2
a
c
cos
β
{\displaystyle b^{2}=a^{2}+c^{2}-2ac\cos \,\beta }
Оттук лесно могат да се изразят и косинусите на дадените ъгли:
cos
α
=
b
2
+
c
2
−
a
2
2
b
c
{\displaystyle \cos \,\alpha ={\frac {b^{2}+c^{2}-a^{2}}{2bc}}}
cos
β
=
a
2
+
c
2
−
b
2
2
a
c
{\displaystyle \cos \,\beta ={\frac {a^{2}+c^{2}-b^{2}}{2ac}}}
cos
γ
=
a
2
+
b
2
−
c
2
2
a
b
{\displaystyle \cos \,\gamma ={\frac {a^{2}+b^{2}-c^{2}}{2ab}}}
Когато един от ъглите на триъгълник е прав, косинусовата теорема се свежда до Питагоровата теорема .
Нека да разгледаме триъгълника
A
B
C
{\displaystyle ABC}
C
{\displaystyle C}
A
B
{\displaystyle AB}
C
D
{\displaystyle CD}
A
D
C
{\displaystyle ADC}
Фиг. 2 . Доказателство на косинусовата теорема.
A
D
=
b
cos
α
{\displaystyle AD=b\cos \,\alpha }
D
B
=
c
−
b
cos
α
{\displaystyle DB=c-b\cos \,\alpha }
Питагоровата теорема за двата триъгълника
A
D
C
{\displaystyle ADC}
B
D
C
{\displaystyle BDC}
{
h
2
=
b
2
−
(
b
cos
α
)
2
h
2
=
a
2
−
(
c
−
b
cos
α
)
2
{\displaystyle {\begin{cases}h^{2}=b^{2}-(b\cos \,\alpha )^{2}\\h^{2}=a^{2}-(c-b\cos \,\alpha )^{2}\end{cases}}}
Очевидно, десните части на двете уравнения са равни, т.е.
b
2
−
(
b
cos
α
)
2
=
a
2
−
(
c
−
b
cos
α
)
2
{\displaystyle b^{2}-(b\cos \,\alpha )^{2}=a^{2}-(c-b\cos \,\alpha )^{2}}
След опростяване се получава
a
2
=
b
2
+
c
2
−
2
b
c
cos
α
{\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \,\alpha }
Въвеждат се базисните вектори
C
B
→
=
a
→
{\displaystyle {\overrightarrow {CB}}={\vec {a}}}
C
A
→
=
b
→
{\displaystyle {\overrightarrow {CA}}={\vec {b}}}
Нека
A
B
→
=
c
→
{\displaystyle {\overrightarrow {AB}}={\vec {c}}}
c
→
=
a
→
−
b
→
{\displaystyle {\vec {c}}={\vec {a}}-{\vec {b}}}
След повдигане на квадрат се достига до равенството
c
→
2
=
a
→
2
+
b
→
2
−
2
(
a
→
⋅
b
→
)
{\displaystyle {\vec {c}}^{2}={\vec {a}}^{2}+{\vec {b}}^{2}-2({\vec {a}}\cdot {\vec {b}})}
От формулата за скаларно произведение на два вектора става ясно, че
‖
c
→
‖
2
=
‖
a
→
‖
2
+
‖
b
→
‖
2
−
2
⋅
‖
a
→
‖
⋅
‖
b
→
‖
cos
∠
(
a
→
,
b
→
)
{\displaystyle \Vert {\vec {c}}\Vert ^{2}=\Vert {\vec {a}}\Vert ^{2}+{\Vert {\vec {b}}\Vert }^{2}-2\cdot \Vert {\vec {a}}\Vert \cdot \Vert {\vec {b}}\Vert \cos \angle ({\vec {a}},\ {\vec {b}})}
С това теоремата е доказана.