Астроида

Забележка: Заглавието на тази статия може лесно да бъде объркано с Астероид.

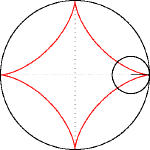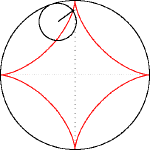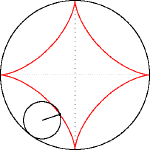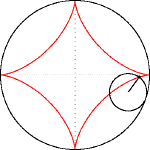
Астроидата е равнинна крива, частен случай на хипоциклоида с четири рогови точки. Може още да се разглежда като супер елипса от степен n=2/3 и с равни оси a и b.

Астроидата се получава като траекторията на фиксирана точка върху окръжност с радиус a/4, която се хлъзга по вътрешността на окръжност с радиус a. Във всяка точка от астроидата ролята на допирателна играе отсечка с дължина a, чийто един край принадлежи на абсцисната, а другия – на ординатната ос в координатната система, чието начало е центърът на астроидата.

Уравнението на астроидата в Декартова координатна система е:

x^{\frac {2}{3}}+y^{\frac {2}{3}}=a^{\frac {2}{3}}

,

а в параметричен вид: ${\begin{cases}x=acos^{3}\varphi \\y=asin^{3}\varphi \end{cases}}$ .

Лицето на областта, заградена от астроидата е $S={\frac {3}{8}}\pi a^{2}$ , а дължината на цялата крива е $L=6a$ .

Наименованието на кривата идва от гръцките думи αστρον – звезда и ειδος – вид, образ. В някои източници кривата се нарича и „звездна крива“. Терминът е въведен от австрийския астроном Йозеф Литров през 1838 г. През 19 век са употребявани различни названия на кривата, които отразяват свойството ѝ, че е еволюта на елипсата.

Източници[редактиране | редактиране на кода]

„The Penguin Dictionary of Mathematics“, John Daintith, R.D. Nelson, Penguin Books, 1989
„Лексикон Математика“, Георги Симитчиев, Георги Чобанов, Иван Чобанов, ИК Абагар, София, 1995, ISBN 954-584-146-X
„Математически термини“, Н. В. Александрова, ДИ Наука и изкуство, София, 1984
„Математически енциклопедичен речник“, В. Гелерт, Х. Кестнер, З. Нойбер, ДИ Наука и изкуство, София, 1983

Външни препратки[редактиране | редактиране на кода]

Страница за астроидата на сайта на Система Mathematica