Радиална скорост
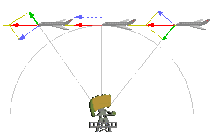
Радиална скорост на обект по отношение на дадена точка е бързината на промяна на разстоянието между обекта и точката. Тоест, радиалната скорост е компонента на скоростта на обекта, която сочи по посока на радиуса, свързващ обекта с точка. В астрономията, точката обикновено се счита за наблюдател на Земята, така че радиалната скорост показва скоростта, с която обектът се отдалечава или приближава Земята.
В астрономията, радиалната скорост често се измерва до първи ред приближение чрез Доплерова спектроскопия. Получената величина по този метод може да се нарече спектроскопична радиална скорост или барицентрична радиална скорост.[1] Обаче, поради релативистичните и космологичните въздействия на големи разстояния, които светлината обикновено прекосява, за да достигне наблюдателя от астрономически обект, тази величина не може да бъде преобразувана с точност до геометрична радиална скорост, без да се вземат предвид допълнителните условия, влияещи на обекта и пространството между него и наблюдателя.[2] В контраст на това, астрометричната радиална скорост се определя чрез астрометрични наблюдения (например, постоянни промени в годишния паралакс).[2][3][4]
Спектроскопична радиална скорост[редактиране | редактиране на кода]

Светлината от обект със значителна относителна радиална скорост при излъчване би била обект на Доплеровия ефект, така че честотата на светлината би намаляла за обекти, които се отдалечават (червено отместване), и би се увеличавала за обекти, които се приближават (синьо отместване).
Радиалната скорост на звезда или друг блестящ отдалечен обект може да се измери точно, като се снеме спектъра с висока резолюция и се сравни измерената дължина на вълната на познатите спектрални линии с дължината на вълната от лабораторни измервания. Положителна радиална скорост означава, че разстоянието между обектите се увеличава или се е увеличавало в миналото, докато отрицателна радиална скорост сочи, че разстоянието между източника и наблюдателя намалява или е намалявало.
При много двойни звезди орбиталното движение обикновено причинява вариации в радиалната скорост от няколко km/s. Тъй като спектърът на тези звезди варира вследствие на Доплеровия ефект, те се наричат спектроскопични двойки. Радиалната скорост може да се използва за изчисляване на съотношението на масите на звезди и някои орбитални елементи, като например ексцентрицитет и голяма полуос. Същият метод се използва и за засичането на планети около звезди – измерването на движението определя орбиталния период на планетата, докато амплитудата на радиалната скорост позволява изчисляването на долната граница на масата на планетата. Методите на радиалната скорост могат да подскажат единствено долната граница, тъй като голяма планета, въртяща се на много голям ъгъл спрямо линията на видимост би влияла на звездата си толкова, колкото и по-малка планета с орбитална равнина на линията на видимостта. Предложено е, че планетите с висок ексцентритет, изчислявани по този начин, всъщност могат да се окажат системи от две планети с кръгла или почти кръгла резонираща орбита.[5][6]
Засичане на екзопланети[редактиране | редактиране на кода]
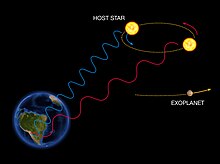
Методът за засичане на екзопланети чрез радиална скорост се основава на засичането на изменения в скоростта на централната звезда, поради променящата се посока на гравитационното привличане от екзопланета, която се върти около звездата. Когато звездата се придвижва към наблюдателя, спектърът ѝ търпи синьо отместване, а когато се отдалечава – спектърът ѝ търпи червено отместване. Чрез редовно наблюдаване на спектъра на звезда и измерването на скоростта ѝ може да се определи дали тя се движи периодично под въздействието на екзопланета.
Съкращаване на данни[редактиране | редактиране на кода]
От инструментална гледна точка, скоростите се измерват по отношение на движението на телескопа. Затова важна първа стъпка е да се съкратят данните, тоест да се премахнат въздействията на:
- Елиптичното движение на Земята около Слънцето (±30 km/s)
- Месечно завъртане от около ±13 m/s на Земята около центъра на гравитация в системата Земя-Луна[7]
- Дневно завъртане на телескопа със земната кора около оста на Земята, което е до ±460 m/s на екватора и пропорционално на косинуса на географската ширина на телескопа
- Малко влияние от полярното движение на Земята от порядъка на mm/s
- Влияние от около 230 km/s от движението около галактичния център[8]
- В случая на спектроскопични измервания – корекции от порядъка на ±20 cm/s по отношение на аберацията[9]
Източници[редактиране | редактиране на кода]
- ↑ Resolution C1 on the Definition of a Spectroscopic „Barycentric Radial-Velocity Measure“. Special Issue: Preliminary Program of the XXVth GA in Sydney, 13 – 26 юли 2003 Information Bulletin n° 91. с. 50. IAU Secretariat. Юли 2002.
- ↑ а б Lindegren, Lennart и др. The fundamental definition of „radial velocity“ // Astronomy and Astrophysics 401 (3). април 2003. DOI:10.1051/0004-6361:20030181. с. 1185 – 1201. Посетен на 4 февруари 2017.
- ↑ Dravins, Dainis и др. Astrometric radial velocities. I. Non-spectroscopic methods for measuring stellar radial velocity // Astron. Astrophys. 348. 1999. с. 1040 – 1051.
- ↑ Resolution C 2 on the Definition of „Astrometric Radial Velocity“. Special Issue: Preliminary Program of the XXVth GA in Sydney, 13 – 26 юли 2003 Information Bulletin n° 91. с. 51. IAU Secretariat. Юли 2002.
- ↑ Anglada-Escude, Guillem и др. How eccentric orbital solutions can hide planetary systems in 2:1 resonant orbits // The Astrophysical Journal Letters 709 (1). 2010. DOI:10.1088/0004-637X/709/1/168. с. 168 – 78.
- ↑ Kürster, Martin и др. Disentangling 2:1 resonant radial velocity oribts from eccentric ones and a case study for HD 27894 // Astron. Astrophys. 577. 2015. DOI:10.1051/0004-6361/201525872. с. A103.
- ↑ Extrasolar Planetary Systems // 2005. DOI:10.1007/10978337_4. с. 219 – 271.
- ↑ Reid, M. J. и др. On the rotation speed of the Milky Way determined from HI emission // The Astrophysical Journal 832 (2). 2016. DOI:10.3847/0004-637X/832/2/159. с. 159.
- ↑ Stumpff, P. Regiorous treatment of the heliocentric motion of stars // Astron. Astrophys. 144. 1985. с. 232.
