Вектор

В математиката и физиката вектори се наричат елементите на линейните пространства. Най-често те се отъждествяват с координатните си представяния като наредени $n$-орки от съответното числово поле. Така евклидовите пространства $\ \mathbb {R} ^{2}$ и $\ \mathbb {R} ^{3}$ се отъждествяват със съответно евклидовите равнина - $(x,y)$, и пространство - $(x,y,z)$, където $x$, $y$ и $z$ са реални числа.

В математиката, физиката и инженерството, евклидов вектор (понякога наричан геометричен или пространствен вектор) или просто вектор е геометричен обект, който има величина (или дължина) и посока и може да бъде добавен към други вектори, съгласно с векторната алгебра. В евклидовата геометрия векторът често се представя от част от линия с определена посока.

Определение

В аналитичната геометрия се използват следните определения за вектор в равнината и пространството. - Отсечка, на която единият край е избран за първи (начало), а другият за втори (край) наричаме насочена отсечка (свързан вектор). Множеството от всички насочени отсечки, равни на дадена насочена отсечка ${\overrightarrow {AB}}$ наричаме вектор (свободен вектор), породен от насочената отсечка ${\overrightarrow {AB}}$. Всяка от тези насочени отсечки ${\overrightarrow {AB}}={\vec {a}}$ наричаме представител на вектора ${\vec {a}}$.

Във всяка точка всеки вектор има точно един представител. Посока и дължина на вектор наричаме посоката и дължината на кой да е негов представител. Нулев вектор ${\vec {0}}$ – има за представител коя да е нулева насочена отсечка, т.е. той няма посока и има дължина 0. За краткост, ако ${\vec {a}}={\overrightarrow {AB}}$ или ${\overrightarrow {AB}}={\vec {a}}$ разбираме, че е даден вектор с представител насочената отсечка ${\overrightarrow {AB}}$, т.е. ${\overrightarrow {AB}}\in {\vec {a}}$

• Нулева насочена отсечка – началната точка А съвпада с крайната точка В
• Ненулева насочена отсечка – началната точка А не съвпада с крайната точка В
• Дължина – на насочената отсечка ${\overrightarrow {AB}}$ наричаме дължината на отсечката $AB$. Бележим $\Vert {\overrightarrow {AB}}\Vert$ или $|{\overrightarrow {AB}}|$.

Елементи на ненулевия вектор

• начало – точка А
• край – точка В
• посока – посоката на лъча ${\overrightarrow {AB}}$
• директриса – правата АВ
• дължина – дължината на АB

Свойства на ненулевите вектори

• Всяка насочена отсечка е равна на себе си;
• Ако ${\overrightarrow {AB}}={\overrightarrow {CD}}$, то и ${\overrightarrow {CD}}={\overrightarrow {AB}}$;
• Ако ${\overrightarrow {AB}}={\overrightarrow {CD}}$ и ${\overrightarrow {CD}}={\overrightarrow {EF}}$, то ${\overrightarrow {AB}}={\overrightarrow {EF}}$.

Насочена права

Ос (насочена права) х наричаме права, на която едната от двете ѝ посоки е избрана за положителна, а другата – за отрицателна.

Алгебрична мярка

Алгебрична мярка (относителна стойност) АВ^— на ненулевата насочена отсечка АВ^→ върху ос наричаме дължина на вектор, взета със знак плюс (+) или минус(-) в зависимост от това дали посоката ѝ съвпада с положителната или отрицателната посока на оста, т.е алгебричната мярка е реално число, като ${\overrightarrow {AB}}=+\Vert {\overrightarrow {AB}}\Vert$ или ${\overrightarrow {AB}}=-\Vert {\overrightarrow {AB}}\Vert$

Действия с вектори

множеството от всички насочени отсечки, равни на дадена насочена отсечка АВ^→

Видове вектори

• Колинеарни вектори са група вектори, които лежат на една права или на успоредни прави. Бележим ${\vec {a}}\parallel {\vec {b}}$.
• Еднопосочни вектори са колинеарни вектори с една и съща посока. Бележим ${\vec {a}}\uparrow \uparrow {\vec {b}}$.
• Противопосочни вектори са колинеарни вектори с различни посока. Бележим ${\vec {a}}\uparrow \downarrow {\vec {b}}$.
• Равни вектори са еднопосочни вектори с равни дължини.
• Противоположни вектори са противопосочни вектори с равни дължини.
• Компланарни вектори са група вектори, които лежат в една равнина или в успоредни равнини. Всяка двойка вектори е компланарна.
• Некомпланарни вектори са група вектори, нележащи в една равнина.

Действия с вектори в равнината

Равенство

${\vec {a}}={\vec {b}}\Leftrightarrow \Vert {\vec {a}}\Vert =\Vert {\vec {b}}\Vert$

Сума

Сборът на векторите ${\vec {a}}$ и ${\vec {b}}$

Сума на два вектора ${\vec {a}}$ и ${\vec {b}}$ наричаме нов вектор, който означаваме с ${\vec {a}}+{\vec {b}}$, и който може да се получи по два начина: по правилото на триъгълника или по правилото на успоредника.

• Правило на триъгълника:

${\overrightarrow {AB}}+{\overrightarrow {BC}}={\overrightarrow {AC}}$

• Правило на успоредника:

${\overrightarrow {AB}}+{\overrightarrow {AD}}={\overrightarrow {AC}}$

За събиране на повече от две вектора се построява представител на всеки следващ вектор с начало във върха на представителя на последния добавен вектор. Сумата от всички вектори има за представител насочената отсечка от началото на първия до върха на последния вектор. Това обобщение на правилото на триъгълника се нарича правило на многоъгълника и намира приложение в статиката при събиране на сили. Пример: ${\overrightarrow {AB}}+{\overrightarrow {BC}}+{\overrightarrow {CD}}+{\overrightarrow {DE}}+{\overrightarrow {EF}}={\overrightarrow {AF}}$.

• Свойства:

${\vec {a}}+{\vec {b}}={\vec {b}}+{\vec {a}}$

$({\vec {a}}+{\vec {b}})+{\vec {c}}={\vec {a}}+({\vec {b}}+{\vec {c}})$

${\vec {a}}+{\vec {0}}={\vec {a}}$

${\vec {0}}+(-{\vec {a}})=-{\vec {a}}$

${\vec {a}}+(-{\vec {a}})={\vec {a}}-{\vec {a}}={\vec {0}}$

Ако векторите ${\vec {a}}$ и ${\vec {b}}$ са зададени с координатите си ${\vec {a}}=(a_{1},\ a_{2},\ a_{3})$ и ${\vec {b}}=(b_{1},\ b_{2},\ b_{3})$ в тримерното пространство, тогава ${\vec {a}}+{\vec {b}}=(a_{1}+b_{1},\ a_{2}+b_{2},\ a_{3}+b_{3})$

Разлика

Разликата на векторите ${\vec {a}}$ и ${\vec {b}}$

Сумата на един вектор ${\vec {a}}$ с противоположния на друг вектор ${\vec {b}}$ наричаме разлика на два вектора. От правилото на триъгълника и правилото на успоредника следва: ${\vec {a}}-{\vec {b}}={\vec {a}}+(-{\vec {b}})$ Ако се построят представители на двата вектора с общо начало, то представител на разликата е насочената отсечка, която съединява върха на втория вектор с върха на първия. Ако векторите ${\vec {a}}$ и ${\vec {b}}$ са зададени с координатите си ${\vec {a}}=(a_{1},\ a_{2},\ a_{3})$ и ${\vec {b}}=(b_{1},\ b_{2},\ b_{3})$ в тримерното пространство, тогава ${\vec {a}}-{\vec {b}}=(a_{1}-b_{1},\ a_{2}-b_{2},\ a_{3}-b_{3})$

Произведение

Произведение на вектор ${\vec {a}}\neq {\vec {0}}$ с число $\lambda \in \mathbb {R}$ наричаме вектора $\lambda {\vec {a}}$ с дължината $\Vert \lambda {\vec {a}}\Vert =\Vert \lambda \Vert \ \Vert {\vec {a}}\Vert$ и с посока:

• $\lambda {\vec {a}}\uparrow \uparrow {\vec {a}}$, ако $\lambda >0$

• $\lambda {\vec {a}}\uparrow \downarrow {\vec {a}}$, ако $\lambda <0$

Ако $\lambda =0$ или ${\vec {a}}={\vec {0}}$, то $\lambda {\vec {a}}={\vec {0}}$.

Свойства на произведението

$\lambda (\mu {\vec {a}})=(\lambda \mu ){\vec {a}}$

$(\lambda +\mu ){\vec {a}}=\lambda {\vec {a}}+\mu {\vec {a}}$

$\lambda ({\vec {a}}+{\vec {b}})=\lambda {\vec {a}}+\lambda {\vec {b}}$

Вектори в пространството

Векторна база в пространството

Определение

Нека ${\vec {a}}{,~}{\vec {b}}{,~}$ и ${\vec {c}}$ са ненулеви вектори в пространството и точка О е произволна точка. Нека ${\overrightarrow {OA}}={\vec {a}}{,~}{\overrightarrow {OB}}={\vec {b}}{,~}{\overrightarrow {OC}}={\vec {c}}{.}$

Векторите ${\vec {a}}{,~}{\vec {b}}{,~}{\vec {c}}{.}$ се наричат компланарни, ако точките О, А, В и С лежат в една или в успоредни равнини.

Ако лежат в различни равнини, те се наричат некомпланарни. Прието е нулевият вектор да е компланарен с произволна двойка вектори.

Два неколинеарни вектора образуват векторна база в равнината, а три некомпланарни вектора образуват векторна база в пространството.

Теореми

Ако векторите ${\vec {a}}{,~}{\vec {b}}{,~}{\vec {c}}$ образуват база $\{{\vec {a}}{;~}{\vec {b}}{;~}{\vec {c}}\}$ в пространството, то за всеки вектор съществува единствено базисно представяне в тази база.

Следствие: Ако $\{{\vec {a}}{;~}{\vec {b}}{;~}{\vec {c}}\}$ е векторна база в пространството, то равенство от вида $\alpha {\vec {a}}+\beta {\vec {b}}+\gamma {\vec {c}}={m}{\vec {a}}+{n}{\vec {b}}+{p}{\vec {c}}$ е възможно тогава и само тогава, когато $\alpha ={m}{,~}\beta ={n}{,~}\gamma ={p}$.

Скаларно произведение на два вектора

Скаларно произведение на два ненулеви вектора ${\vec {a}}$ и ${\vec {b}}$ е числото $\Vert {\vec {a}}\Vert \ \Vert {\vec {b}}\Vert \ \cos {\angle {({\vec {a}},\ {\vec {b}})}}$, където $\cos {\angle {({\vec {a}},\ {\vec {b}})}}$ е косинусът на ъгъла между двата вектора, a $\Vert {\vec {a}}\Vert$ и $\Vert {\vec {b}}\Vert$ са дължините на векторите. Ъгълът може да приема стойности в интервала $\left[{0^{\circ },\ 180^{\circ }}\right]$. Лесно може да се покаже, че ${\vec {a}}\perp {\vec {b}}\Leftrightarrow {\vec {a}}{.}{\vec {b}}=0$

Ако векторите ${\vec {a}}$ и ${\vec {b}}$ са с координати ${\vec {a}}=(a_{1},\ a_{2},\ a_{3})$ и ${\vec {b}}=(b_{1},\ b_{2},\ b_{3})$ в тримерното пространство, то:

${\vec {a}}{.}{\vec {b}}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$

Векторно произведение на два вектора

Илюстрация на векторното проезведение на ${\vec {a}}$ и ${\vec {b}}$

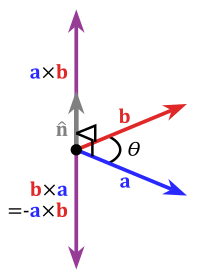
Векторно произведение на два вектора е вектор, чиято дължина е равна на произведението от дължините на двата вектора и синусът на ъгъла между тях. Самото векторно произведение се дефинира така: ${\vec {a}}\times {\vec {b}}=\Vert {\vec {a}}\Vert \ \Vert {\vec {b}}\Vert \sin \angle ({\vec {a}},\ {\vec {b}})\ \mathrm {\hat {n}}$, където с $\mathrm {\hat {n}}$ е отбелязан единичният вектор, перпендикулярен на ${\vec {a}}$ и ${\vec {b}}$.

Нека векторите ${\vec {a}}$ и ${\vec {b}}$ са зададени с координатите си ${\vec {a}}=(a_{1},\ a_{2},\ a_{3})$ и ${\vec {b}}=(b_{1},\ b_{2},\ b_{3})$ в тримерното пространство и ${\vec {i}},{\vec {j}},{\vec {k}}$ са единичните вектори на дясно ориентирана ортонормирана координатна система. Тогава векторното произведение изглежда така:

${\vec {a}}\times {\vec {b}}=\mathrm {det} \left({\begin{matrix}{\vec {i}}&{\vec {j}}&{\vec {k}}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{matrix}}\right)$.