Граница (математика)

Вижте пояснителната страница за други значения на Граница.

---

Граница в математиката е стойността, до която дадена функция или числова редица се доближава, когато аргументът се доближава до някаква стойност. Границите са важна част от математическия анализ и се използват за определяне на непрекъснатост, производни и интеграли.

Формулата за граница на функция обикновено се записва по следния начин:

$\lim _{x\to c}f(x)=L$,

и се чете: границата на f от x, когато x се доближава до c, е равна на L. Фактът, че функцията f се доближава до лимита L, когато x се доближава до c, понякога се записва със стрелка, например:

$f(x)\to L{\text{ as }}x\to c.$

Граница на функция

Винаги, когато точка x е в δ от c, f(x) е в ε единици от L.		За всяко x > S, f(x) е в ε на L.

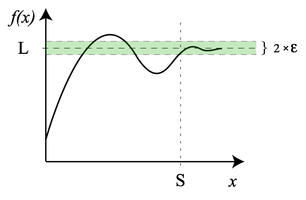
Нека $f$ да е реална функция, а $c$ – реално число. Интуитивно, записът

$\lim _{x\to c}f(x)=L$

означава, че $f(x)$ може да бъде много близо до $L$, като доближим $x$ достатъчно близо до $c$. В този случай, по-горното уравнение се чете по следния начин: „границата на $f$от $x$, когато $x$ клони към $c$, е $L$“.

През 1821 г. Огюстен Луи Коши, следван от Карл Вайерщрас, формализира дефиницията на границата на функция, която става известна като (ε, δ)-дефиниция на граница. Дефиницията използва ε (малка буква епсилон в гръцката азбука), за да обозначи кое да е малко положително число, така че „$f(x)$да се доближи до $L$“ да означава, че $f(x)$лежи в интервала $(L-\epsilon ,L+\epsilon )$, което може да се запише и със знака за абсолютна стойност – $|f(x)-L|<\epsilon$. Тогава изказът „когато $x$ клони към $c$“ индикира, че се отнасяме към стойностите на $x$, чието разстояние от $c$ е по-малко от някое положително число δ (малка буква делта от гръцката азбука), т.е. стойностите на $x$ при $(c-\delta ,c)$ или $(c,c+\delta )$, може да се изрази с $0<|x-c|<\delta$. Първото неравенство означава, че разстоянието между $x$ и $c$ е по-голямо от $0$ и, че $x\neq c$, а следващото неравенство показва, че $x$ е на разстояние $\delta$ от $c$.

Горната дефиниция на лимита е вярна, дори ако $f(c)\neq L$. Функцията $f$ не е необходимо да бъде дефинирана при $c$.

Например, ако

$f(x)={x^{2}-1 \over x-1}$

то тогава $f(1)$ не е дефинирана (виж делене на нула), но когато $x$ се доближава до 1, $f(x)$ се доближава до 2:

f(0.9)	f(0.99)	f(0.999)	f(1.0)	f(1.001)	f(1.01)	f(1.1)
1.900	1.990	1.999	⇒ недефинирана ⇐	2.001	2.010	2.100

Функцията sinx/x

Граница се въвежда и ако директното пресмятане на стойността на функция в разглеждана точка води до неопределеност от типа 0/0. Например директното пресмятяне на стойността на функцията

${\frac {\sin x}{x}}$

за $x=0$ води до резултат 0/0, който не е еднозначно дефиниран. Но ако изчислим стойността на същата функция за стойности на $x$, близки до 0, например 0,0001, ще получим 1, т.е.

$\lim _{\Delta x\rightarrow 0}f(x)=1$.

Функцията tg x

Лява и дясна граница на функция

В много случаи независимата променлива х клони към х₀ чрез растящи редици от стойности, т.е. отляво, или чрез намаляващи редици от стойности, т.е. отдясно. Получените граници в тези случаи се наричат лява и дясна граница на функцията в зависимост от това дали аргументът остава съответно по-малък, или по-голям от стойността, към която клони. Бележат се със:

$\lim _{x\rightarrow x_{0}-}f(x)$ за лява граница и

$\lim _{x\rightarrow x_{0}+}f(x)$ за дясна граница.

Лява и дясна граница се определят в случаите, когато тези две стойности са различни – тогава функцията е прекъсната в дадената точка. Например лявата и дясната граница на функцията $tgx$ при $x$, клонящо към $90^{\circ }$, са съответно $+\infty ;-\infty$.

Неистинска граница на функция

Казва се, че функцията $f(x)$ има неистинска граница $+\infty$ или $-\infty$, ако за всяко произволно голямо число $C>0$ съществува такова число $\delta (''C'')>0$, че за всички $x$, за които $0<|x-a|<\delta$, е изпълнено неравенството $f(x)>C$, съответно f(x) < -C$f(x)<-C$. Означава се:

$\lim _{x\rightarrow a}f(x)=+\infty ;$, $\lim _{x\rightarrow a}f(x)=-\infty$.

Поведение на функциите в безкрайността

Поведението на дадена функция $f(x)$за много големи положителни и много малки отрицателни стойности на аргумента $x$ се определя със следните дефиниции:

Казва се, че

$\lim _{x\rightarrow \infty }f(x)=A,$ и съответно $\lim _{x\rightarrow -\infty }f(x)=A,$

ако за произволно отнапред дадено $\epsilon >0$съществува такова достатъчно голямо $x_{0}>0$, че $|f(x)-A|<\epsilon$ за всички $x>x_{0}$ или съответно за всички $x<-x_{0}$.

Граница на числова редица

Граница на дадена числова редица $(a_{n})$ е число $l$ точно тогава, когато за всяко произволно малко положително число $\epsilon >0$ може да се намери такова число N(ε), че всички членове а_n на редицата с номера n > N(ε) да попадат в интервала (l – ε, l + ε), т.е. да е изпълнено |a_n – l| < ε за всички n > N(ε).

$\lim _{n\to \infty }a_{n}=l.$

С формализма на математическата логика това се записва по следния начин:

$\forall \epsilon >0,\exists N(\epsilon )\in \mathbb {N} \,:\,\forall n>N(\epsilon ),\|a_{n}-l\|<\epsilon .$

Еквивалентно, но по-интуитивно определение е следното: Дадено число $l$ е граница на числовата редица $(a_{n})$, ако всяка околност („всяка околност“ е интервалът $(l-\epsilon ,l+\epsilon )$ за произволно $\epsilon >0$) съдържа всички членове на редицата с изключение на краен брой.

Ако дадена числова редица притежава граница, тогава редицата се нарича сходяща. В противен случай тя е разходяща. Понякога сходяща числова редица с граница нула се нарича нулева или безкрайно малка редица.

Например границата на редицата

$1,{\frac {1}{2}},{\frac {1}{3}},...,{\frac {1}{n}},...$

при n, клонящо към безкрайност (бележи се n → ∞), е 0, тъй като колкото повече n расте, толкова повече ${\frac {1}{n}}$ намалява (и все повече се доближава до 0).

Редицата $1,-1,1,...,(-1)^{n-1},...$ няма граница, понеже има две точки на сгъстяване: -1 и +1. За нито една от тези точки не е изпълнено условието „Всяка околност съдържа всички членове на редицата освен някакъв краен брой“, понеже съществуват две точки, всяка околност на които съдържа безкраен брой членове на редицата: -1 и 1. Редицата е ограничена и отгоре, и отдолу, т.е. съгласно теоремата на Болцано – Вайерщрас съществуват две числови редици: а_{2n} (всички четни членове на редицата) и а_{2n+1} (всички нечетни членове на редицата), които са сходящи: границите им са съответно +1 и -1.

Свойства на границите на редици

• Ако редиците (a_n), (b_n) и (c_n) са сходящи и клонят съответно към a, b, c, то

$\lim _{n\to \infty }(a_{n}+b_{n})=\lim _{n\to \infty }a_{n}+\lim _{n\to \infty }b_{n}.$

$\lim _{n\to \infty }(a_{n}-b_{n})=\lim _{n\to \infty }a_{n}-\lim _{n\to \infty }b_{n}.$

$\lim _{n\to \infty }(a_{n}.b_{n})=\lim _{n\to \infty }a_{n}.\lim _{n\to \infty }b_{n}.$

$\lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}={\frac {\lim _{n\to \infty }a_{n}}{\lim _{n\to \infty }b_{n}}}.$

за b_n ≠ 0 и $\lim _{n\to \infty }b_{n}$ ≠ 0.

$\lim _{n\to \infty }ca_{n}=c\lim _{n\to \infty }a_{n}$ за c = const.

$\lim _{n\to \infty }(c_{1}a_{n}+c_{2}b_{n})=c_{1}\lim _{n\to \infty }a_{n}+c_{2}\lim _{n\to \infty }b_{n}$

при с₁ = const, c₂ = const.

$\lim _{n\to \infty }\log _{b}a_{n}=log_{b}a$ при b > 0, a > 0, b ≠ 1.

$\lim _{n\to \infty }{a_{n}}^{p}=a^{p}$ при а > 0 и произволно р.

Основни теореми за граници на редици

• Всяка сходяща числова редица е ограничена, но не всяка ограничена числова редица е сходяща.
• Границата на всяка сходяща числова редица е еднозначно определена. Тя не може да има две различни граници.
• Ако за всички членове на сходящата редица (а_n) при $n\geq n_{0}$ са изпълнени неравенствата $A\leq a_{n}\leq B,$ то тези неравенства са изпълнени и за границата а на редицата: $A\leq a\leq B.$
• Ако $a_{n},b_{n},c_{n}$ са три сходящи редици, такива че $\lim _{n\to \infty }a_{n}=\lim _{n\to \infty }c_{n}=d$ и $a_{h}\leq b_{h}\leq c_{h}$$\forall h$, то $\lim _{n\to \infty }b_{n}=d$.

Вижте също

• Функция
• Математически анализ
• Сходимост
• Редица на Коши
• Граница на функция

Източници

Тази страница частично или изцяло представлява превод на страницата Limit (mathematics) в Уикипедия на английски. Оригиналният текст, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за съдържание, създадено преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналната страница, както и на преводната страница, за да видите списъка на съавторите. ​ ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни.​