Ортоцентър

Трите височини на всеки триъгълник се пресичат в една точка, която се нарича ортоцентър. Ортоцентърът лежи вътре в триъгълника, само ако той е остроъгълен (трите му вътрешни ъгли са по-малки от 90°). Когато триъгълникът е тъпоъгълен, ортоцентърът лежи вън от него, а когато е правоъгълен – съвпада с върха, при който е правият ъгъл.

Свойства

Трите височини в един триъгълник се пресичат в една точка

Ще разгледаме две доказателства. Нека $AM\perp BC$, $BN\perp AC$ и $AM\cap BN=\{H\}$.

Доказателство с окръжности

Означаваме $\angle BAM=\alpha$. Понеже $\angle ANB=\angle AMB$, то четириъгълникът $ABMN$ е вписан в окръжност. Тогава $\angle BAM=\angle BNM=\alpha \ (1)$. В четириъгълникът $HMCN$, $\angle HMC+\angle HNC=180^{\circ }$, следователно и той е вписан. Това означава, че $\angle HNM=\angle HCM=\alpha \ (2)$. От $(1)$ и $(2)$ става ясно, че $\angle BAM=\angle HCM=\alpha$. Нека сега $CH\cap AB=\{P\}$. В триъгълник $PBC$, $\angle PCB=\alpha$ и $\angle PBC=90^{\circ }-\alpha$, следователно $\angle CPB=90^{\circ }$. С това доказахме, че трите височини се пресичат в една точка.

Доказателство с вектори

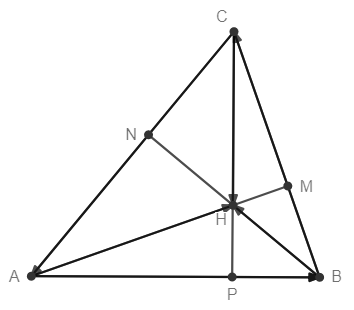
Този път ще използваме тъждеството на Ойлер. Имаме${\overrightarrow {CA}}\cdot {\overrightarrow {BH}}+{\overrightarrow {BC}}\cdot {\overrightarrow {AH}}+{\overrightarrow {AB}}\cdot {\overrightarrow {CH}}={\overrightarrow {0}}$Понеже скаларното произведение на два перпендикулярни вектора е равно на нула, то стигаме до извода, че

${\overrightarrow {AB}}\cdot {\overrightarrow {CH}}=0$

откъдето и

${\overrightarrow {AB}}\perp {\overrightarrow {CH}}$

Следователно трите височини се пресичат в една точка.

Еднакви окръжности

Нека $H$ е ортоцентърът на триъгълник $ABC$. Тогава окръжностите, описани около триъгълниците $ABH$ и $ABC$, са еднакви.

Доказателство

Нека $\angle ACB=\gamma$. Тогава $\angle NHM=360^{\circ }-2\cdot 90^{\circ }-\gamma =180^{\circ }-\gamma =\angle AHB$. Прилагаме синусовата теорема за триъгълниците $ABC$ и $ABH$:

${\begin{cases}{\dfrac {AB}{\sin \gamma }}=2R_{ABC}\\{\dfrac {AB}{\sin(180^{\circ }-\gamma )}}=2R_{ABH}\end{cases}}$

където $R_{ABH}$ и $R_{ABC}$ са радиусите на окръжностите, описани съответно около триъгълниците $ABH$ и $ABC$.

Но $\sin(180^{\circ }-\gamma )=\sin \gamma$, следователно системата придобива следния вид:

${\begin{cases}{\dfrac {AB}{\sin \gamma }}=2R_{ABC}\\{\dfrac {AB}{\sin \gamma }}=2R_{ABH}\end{cases}}$

откъдето става ясно, че $R_{ABH}=R_{ABC}$, т.e. окръжностите са еднакви.

Аналогично може да се покаже, че $R_{ABC}=R_{BCH}$ и $R_{ABC}=R_{AHC}$

Права на Ойлер

Ортоцентърът, центърът на описана окръжност, медицентърът и центърът на Окръжността на деветте точки лежат на една права - права на Ойлер. Центърът на Окръжността на деветте точки съвпада със средата на отсечката, свързваща ортоцентъра с центъра на описаната окръжност, а разстоянието между медицентъра и центъра на описаната окръжност е половината от това между медицентъра и ортоцентъра.