Число на завъртане

В математиката число на завъртане или индекс на въртене на затворена крива около дадена точка на наблюдение в равнина е цяло число, представляващо броя на пълните обороти, които кривата прави около точката обратно на часовниковата стрелка.

Тази крива има обща кривина 6π и число на връщанията 3, въпреки че има само 2 оборота около p.

Нарича се още ред на кривата или индекс на кривата и може да се изчисли като общата кривина, разделена на 2π. Броят на оборотите зависи от ориентацията на кривата спрямо точката и е отрицателен, ако кривата се движи около точката по посока на часовниковата стрелка. Тогава се говори за отрицателен ред на кривата спрямо точката.

Може също така да се вземе предвид индексът на въртене на пътя по отношение на тангентата на самия път. Като път, следван във времето, това би било числото на завъртане по отношение на началото на вектора на скоростта. Това е дефинирано само за пътища по гладки криви без начупени линии (т. е. за диференцируеми пътища с неизчезващи никъде производни) и е степента на тангенциалната карта на Гаус.

Числата на завъртане на кривите спрямо точки са основни обекти на изследване в алгебричната топология и също така играят важна роля във векторния анализ, комплексния анализ, геометричната топология, диференциалната геометрия и физиката, включително теорията на струните.

В същия смисъл се използва и понятието индекс на точката спрямо кривата.

Интуитивно описание

Обект, който се движи по червената крива, прави две завъртания обратно на часовниковата стрелка около наблюдателя в началото.

Нека е дадена затворена, ориентирана крива в равнината xy. Кривата може да се представи като пътя на движение на някакъв обект и ориентацията на кривата показва посоката, в която се движи обектът. Тогава числото на завъртане на кривата е равно на общия брой завъртания обратно на часовниковата стрелка, които обектът прави около началото.

Когато се броят завъртанията, движението обратно на часовниковата стрелка се счита за положително, докато движението по часовниковата стрелка се счита за отрицателно. Например, ако обектът първо обиколи началото 4 пъти обратно на часовниковата стрелка и след това го обиколи веднъж по посока на часовниковата стрелка, тогава общият брой на навиване на кривата е 3.

Според тази схема крива, която изобщо не се движи около точката на наблюдателя, има индекс (ред) на въртене нула, а крива, която се движи по посока на часовниковата стрелка около точката, има отрицателен индекс на въртене. Индексът на завъртане на крива може да бъде всяко цяло число. Следващите фигури показват криви с числа на завъртане между −2 и 3:

$\cdots$
	−2	−1	0
				$\cdots$
	1	2	3

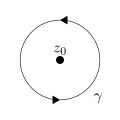
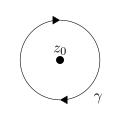
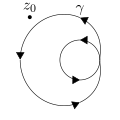
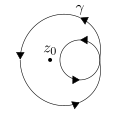
Числото на завъртане зависи не само от начина на описване на кривата, но и от мястото на точката на наблюдателя спрямо кривата. Ако един от тези два фактора се променя, а другият остава постоянен, числото на завъртане се изменя:

Число на завъртане / индекс на въртене / ред на кривата

1	−1	0	1	2

Определения

Съществуват различни определения за понятието число на завъртане или индекс на въртене (ред на крива), като най-точният термин зависи от конкретния случай.

Формално определение

Крива в равнината xy може да се дефинира чрез параметрични уравнения:

$x=x(t)\quad {\text{и}}\quad y=y(t)\quad {\text{за}}\quad 0\leq t\leq 1.$

Ако се избере параметъра t като време, тези уравнения определят движението на обект в равнина между t = 0 и t = 1. Пътят на това движение е крива, ако функциите x(t) и y(t) са непрекъснати. Тази крива е затворена, ако позицията на обекта е една и съща в моменти t=0 и t=1.

Може да се определи индекса на такава крива спрямо точка, използвайки полярната координатна система. Ако се приеме, че кривата не минава през точката на наблюдение, може да се пренапишат параметричните уравнения:

$r=r(t)\quad {\text{и}}\quad \theta =\theta (t)\quad {\text{за}}\quad 0\leq t\leq 1.$

Функциите r(t) и θ(t) трябва да са непрекъснати с r > 0. Тъй като началната и крайната точки са еднакви, θ(0) и θ(1) трябва да се различават с кратно на 2π. Тази стойност е индексът на въртене:

$Io={\frac {\theta (1)-\theta (0)}{2\pi }}.$

Това определение дава индекса на началото на равнината xy. Чрез трансформиране на координатната система тази дефиниция може да бъде разширена до всяка точка на наблюдение.

Други определения

• В диференциалната геометрия параметричните уравнения обикновено се приемат за диференцируеми (гладки) или поне частично диференцируеми. В този случай полярната координата θ е свързана с декартовите координати x и y чрез уравнението:

$d\theta ={\frac {1}{r^{2}}}\left(x\,dy-y\,dx\right),$  където  $r^{2}=x^{2}+y^{2}.$

Според теоремата на Нютон—Лайбниц общата промяна θ е равна на интеграла dθ. По този начин индексът на гладка крива спрямо точка се изразява чрез криволинеен интеграл:

$Io={\frac {1}{2\pi }}\oint _{C}\,{\frac {x}{r^{2}}}\,dy-{\frac {y}{r^{2}}}\,dx.$

• В комплексния анализ индексът на въртене $Io$ на затворена крива $C$ в комплексната равнина спрямо точка с комплексни координати $z=x+iy$ се определя от израза

$Io={\frac {1}{2\pi i}}\oint _{C}{\frac {dz}{z}}.$

• В топологията числото на завъртане е алтернативно понятие за степента на изображение. Във физиката числото на завъртане често се нарича ​​топологично квантово число или топологичен заряд. И в двата случая се използва една и съща концепция.

Границите на правилен звезден деветоъгълник {9/4} обикалят центъра 4 пъти, така че той има плътност 4

• В многоъгълниците числото на завъртане определя „плътността“ на многоъгълника – броят на завъртанията около центъра на n-ъгълника, които се правят при начертаването му с n прави линии. За изпъкнали многоъгълници, както и за прости многоъгълници (несамопресичащи се), плътността е 1 по теоремата на Жордан. Правилен звезден многоъгълник, означен със символа на Шлефли {p/q} има p върха и плътност q.

Този раздел е празен или е мъниче. Можете да помогнете на Уикипедия, като го разширите.

Външни препратки

• Winding numberАрхив на оригинала от 2019-05-27 в Wayback Machine. на сайта PlanetMath.