Аристарх Самоски
- Вижте пояснителната страница за други личности с името Аристарх.
| Аристарх Самоски Ἀρίσταρχος ὁ Σάμιος | |
| древногръцки астроном | |
 | |
| Роден |
ок. 310 пр.н.е.
|
|---|---|
| Починал | ок. 230 пр.н.е.
Александрия, Гърция |
| Научна дейност | |
| Област | Астрономия, математика |
| Аристарх Самоски в Общомедия | |
Аристарх Самоски (на старогръцки: Ἀρίσταρχος ὁ Σάμιος) e древногръцки астроном и математик от III век пр. Хр..
Аристарх е ученик на Странон от Лампсак, който му оказва голямо влияние. Едно от най-важните достижения на Аристарх е разработването на хелиоцентрична система, според която центърът на Вселената не е Земята, а Слънцето. Поради тези си възгледи Аристарх понякога е наричан „Коперник на древността“.[1] Възможно е подобна теза да са изказвали и други астрономи от Античността, но Аристарх е първият, за когото това е известно с необходимата сигурност. Теорията му не е намерила подкрепа сред съвременниците му, с изключение на Селевк. Трябвало е да минат около 2000 години, за да може идеята за хелиоцентризма да намери подобаващо развитие.
Хелиоцентризъм[редактиране | редактиране на кода]
Изглежда че Аристарх е първият, изказал хипотезата, че Земята обикаля около Слънцето.[2] Съчиненията на Аристарх по този въпрос не са достигнали до нас, но неговата хипотеза се цитира от Плутарх, Секст Емпирик, както и от самия Архимед. Плутарх в своето съчинение „За лицето на видимата страна на Луната“ пише: „Този човек (Аристарх Самоски) се опитва да обясни небесните явления с предположението, че небето е неподвижно, а Земята се движи [по еклиптиката], като същевременно се върти около оста си“. Самият Архимед пише в съчинението си „Пресмятане на песъчинките“: „Аристарх Самоски, в своите „Предположения“ смята, че неподвижните звезди и Слънцето не менят положението си в пространството, а Земята се движи по окръжност, в чиито център се намира Слънцето, и че центърът на сферата на неподвижните звезди съвпада с този на Слънцето“.
Причините, поради които Аристрах е изложил хелиоцентричната си теория, са неясни, но най-вероятно той е смятал, че не е логично голямо тяло като Слънцето (вж. по-долу) да обикаля около Земята. Благодарение на Архимед познаваме и друг важен извод, до който е достигнал Аристарх, а именно, че звездите трябва да са изключително далеч от нас, което да обяснява факта, че годишните им паралакси не се наблюдават с просто око, а такива трябва да съществуват при движение на Земята около Слънцето.
„За размерите и разстоянията до Слънцето и Луната“[редактиране | редактиране на кода]
От съчиненията на Аристарх до нас е достигнало само „За размерите и разстоянията до Слънцето и Луната“, което представлява първия опит в историята на науката да се определят тези величини. Разбира се, и други гръцки философи са се изказвали по въпроса за размера на Слънцето: Хераклит считал, че Слънцето е с размерите на стъпало, колкото е и видимия му размер,[3] а Анаксагор смятал, че Слънцето дори е по-голямо от Пелопонес,[4] но тези предположения нямали абсолютно никаква научна обосновка. За разлика от тях Аристарх приложил научен метод, като наблюдавал фазите на Луната и лунните и слънчевите затъмнения.
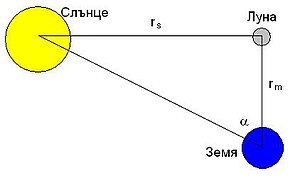
За да се измери отношението на разстоянията Земя-Луна (rm) и Земя-Слънце (rs), е необходимо да се знае tan α (вж. схемата вляво). Построенията му се основават на твърдението, че Луната не свети със собствена светлина, а отразява тази на Слънцето, т.е. при квадратура ъгълът Земя-Луна-Слънце е прав. При това положение показаното положение на светилата отговаря на момента, когато Луната е във фаза първа или последна четвърт. Аристарх измерил ъгловото разстояние между Слънцето и Луната, когато тя се намира във фаза първа четвърт, и установил, че е приблизително равно на 19, т.е. Слънцето е 19 пъти по-далеч от Луната.[5] Разбира се, Аристарх не е познавал тригонометрията, т.е. не е знаел, че , а е извел това отношение с по-сложни методи. Точната стойност е 89°30', което дава отношение на разстоянията от около 380 пъти. Аристарх е приложил вярна геометрия, но върху неточни данни. Причината за грешката е неточността, с която се е определял моментът на квадратурата по това време.
Взаимните размери на Слънцето и Луната Аристарх установил на базата на наблюдения на слънчеви затъмнения: при слънчево затъмнение Луната покрива точно Слънчевия диск, т.е. те имат еднакви ъглови размери, или отношението на линейните им размери е равно на отношението на разстоянията до тях. Следователно, заключава Аристарх, Слънцето е 19 пъти по-голямо от Луната,[5] което е неточно, но следва логически от предните му разсъждения.
Следващата стъпка била измерването на размерите на Слънцето и Луната към тези на Земята. За това Аристарх започнал наблюдения на лунните затъмнения. Причината за това била ясна: при лунно затъмнение Луната попада в земната сянка. За изчисляването на размера на Луната спрямо този на Земята Аристарх е използвал метод, подобен на следния:[6] Първо, построяваме схемата на лунното затъмнение:
Обозначения:
| s | Радиус на Слънцето |
| S | Разстояние до Слънцето |
| l | Радиус на Луната |
| L | Разстояние до Луната |
| t | Радиус на Земята |
| D | Разстояние от центъра на Земята до върха на земната сянка |
| n | d/l, директно наблюдаема по време на лунно затъмнение величина |
| директно наблюдаема величина | |
| ъглов радиус на Слънцето и Луната | |
| x | S/L, извежда се от |
От подобните триъгълници следва: и
Поради факта, че Слънцето и Луната са с еднакви ъглови размери: . Следователно:
Ако положим , става известно опростяване:
Което дава отношението на радиусите на Слънцето и Луната изцяло като функция от наблюдаеми величини. Също така тези формули дават разстоянията до Слънцето и Луната като функция от земния радиус:
Аристарх не е познавал точната стойност на числото π, но дори и при π=3 грешката е в рамките на 5%.
Този метод е добро приближение на метода, използван от Аристарх.[6]
Други работи[редактиране | редактиране на кода]
Аристрарх е един от предшествениците на тригонометрията, като доказва неравенствата: . Също така се е занимавал с оптика, като е изказал предположението, че предметите дължат цветовете си на светлината, която пада върху тях, понеже на тъмно предметите изглеждат безцветни.
За нуждите на календара той предлага своята „Голяма година на Аристарх“, която съдържа точно 270 сароса или 4868 години. Той дефинирал и месеца, който вавилонците използвали, на базата на относително стабилния цикъл от затъмнения от 4267 месеца, като отклоненията в дължината на един месец били по-малко от стотни от секундата в различните цикли.
Външни препратки[редактиране | редактиране на кода]
- Аристрах Самоски (The MacTutor History of Mathematics archive)
- Разстоянието до Луната според Аристарх
- Страница на Dennis Rawlins
- A. H. Batten: Аристарх Самоски
- Аристарх и размерите на Луната
- H. Thurston: Greek Mathematical Astronomy Reconsidered Архив на оригинала от 2004-02-27 в Wayback Machine.
- Gomez, A. G. Aristarchos of Samos, the Polymath. AuthorHouse, 2013. ISBN 978-1-4817-8949-3.
Източници[редактиране | редактиране на кода]
- ↑ The Ancient Copernicus Архив на оригинала от 2007-07-16 в Wayback Machine., Sir Thomas Heath, Dover Publications, ISBN 0-486-43886-4
- ↑ S V Zhitomirskii, The heliocentric hypothesis of Aristarchos of Samos and ancient cosmology (Russian), Istor.-Astronom. Issled. No. 18 (1986), 151 – 160.
- ↑ Outline of Cosmology and Astronomy to Aristarchus
- ↑ The Pre Socratic Philosophers by G.S. Kirk, J.E. Raven and M.Schofield, Cambridge University Press, New York, Second Edition 1983, p381
- ↑ а б van Helden, A. Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley. Chicago: Univ. of Chicago Pr., 1985. ISBN 0-226-84882-5.
- ↑ а б Heath, T. L. Aristarchus of Samos. Oxford, 1913. Второ издание: (ISBN 0-486-43886-4).
| Тази страница частично или изцяло представлява превод на страницата „Аристарх Самосский“ и страницата „Aristarchus On the Sizes and Distances“ в Уикипедия на руски и английски език. Оригиналните текстове, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за творби създадени преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналните страници тук и тук, за да видите списъка на техните съавтори.
ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни. |



















