Ентропия
| Серия статии на тема Статистическа физика |

Формализъм
Статистически ансамбли
Квантови статистики
Потенциали
Газове от частици
Известни модели
|
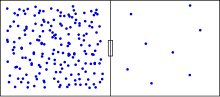

Ентропия е физична величина, която представлява мярка за безпорядъка на термодинамичните системи. Терминът „ентропия“ произхожда от гръцкия език: εν – вътре, τρέπω – пренасям.[1]
Ентропията характеризира състоянието на термодинамичната система, т.е. зависи само от текущото състояние, а не от това как системата се е озовала в него.
Ентропията е правопропорционална на логаритъма на броя на възможните микросъстояния (конфигурации на градивните частици), съответстващи на дадено макросъстояние на системата. Състоянието на термодинамично равновесие се характеризира с максимална вероятност, максимален безпорядък и максимална ентропия.
Различия с други величини[редактиране | редактиране на кода]
Вътрешната енергия на системата включва общото количество механична енергия на градивните частици, докато ентропията отчита качественото различие между насочено и хаотично движение на същите частици.
Работата и количеството топлина характеризират процесите, които протичат в системата, а ентропията характеризира състоянието на системата.
Ентропията се различава и от температурата: например при изотермно нагряване температурата остава постоянна, а ентропията на системата нараства.
Газовете имат по-голяма ентропия от течностите и твърдите тела.
Основна закономерност[редактиране | редактиране на кода]
Ако в изолирана макроскопична система протича термодинамичен процес, то ентропията на системата нараства и процесът е необратим. Всички процеси в природата се подчиняват на този закон (втори принцип на термодинамиката).
История[редактиране | редактиране на кода]
Понятието „ентропия“ е въведено за първи път през 1865 г. от Рудолф Клаузиус (1822-1888), немски физик, считан за един от създателите на термодинамиката и кинетичната теория на газовете. Той предлага и една от формулировката на втория принцип на термодинамиката.
Теория[редактиране | редактиране на кода]
Класическа термодинамика[редактиране | редактиране на кода]
Изменението на ентропията ΔS на термодинамична система при обратими процеси е отношението на изменението на общото количество топлина ΔQ към абсолютната температура Т.
Ентропията се измерва в J/K, а специфичната ентропия – в J/(kg.K).
Названието „ентропия“ е предложено от Клаузиус.
Тази формула е приложима само за изотермни процеси. Обобщението ѝ за произволен квазистатичен процес изглежда така:
- ,
където dS е диференциалът на ентропията, а δQ е безкрайно малко количество топлина. Ентропията е характеристика на състоянието, затова в лявата част на равенството стои пълен диференциал. Обратно, количеството топлина е характеристика на процеса, а не на състоянието, затова δQ е непълен диференциал.
Горната формула определя единствено изменението на ентропията, следователно задава ентропията с точност до едно неизвестно събираемо (т. нар. нулево ниво). Третият принцип на термодинамиката допълва определението на ентропията, като уточнява нейното нулево ниво: при температура, равна на абсолютната нула, ентропията на равновесна система също е нула. Това е така, тъй като абсолютната нула на температурата съответства на прекратяване на хаотичното движение на градивните частици на веществото.
Статистическа термодинамика[редактиране | редактиране на кода]
През 1877 г. Лудвиг Болцман открива, че ентропията S на една система е пропорционална на логаритъма от броя Ω на възможните микросъстояния, съответстващи на дадено макроскопично състояние. В случая на идеален газ микросъстоянието се определя от местоположението и импулса на всяка от градивните частици на системата.
Болцман е установил, че
- ,
където k = 1,38.10-23 J/К е т. нар. константа на Болцман. Тази формула е част от статистическата термодинамика, която описва термодинамичните системи чрез поведението на съставящите ги компоненти. Формулата на Болцман свързва микроскопичните свойства на системата (броя Ω на микросъстоянията) с едно от нейните макроскопични термодинамични свойства (ентропията S).
От формулата на Болцман се вижда, че ентропията е функция на състоянието. Тъй като Ω може да бъде само естествено число (1, 2, 3 и т.н.), то ентропията може да приема само неотрицателни стойности.



