Логаритъм
Логаритъм (на старогръцки λόγος – „отношение“ + ἀριθμός – „число“[1][2]) на дадено число е показателят на степента , на която трябва да бъде повдигната основата , за да се получи числото . Логаритъмът от с основа се записва като logb (x) или без скоби, като logb x; и дори без уточняване на основата, като log x, когато не може да стане объркване. Изчисляването на логаритъма се нарича логаритмуване и е математическа функция, обратна на степенуването.


От определението в явен вид връзката между логаритъм и степен е:
- тогава и само тогава, когато .
Например, log2 64 = 6, тъй като 64 = 26.
В най-простия случай логаритъмът е броят на еднаквите множители в произведение от еднакви множители. Например, тъй като 1000 = 10 × 10 × 10 = 103, логаритъмът с основа 10 на 1000 е 3.
По-общо, степенуването позволява всяко положително реално число да бъде повдигнато на всяка реална степен, като резултатът е винаги положителен, така че логаритъмът на всеки две положителни реални числа и , където е различно от 1, е винаги уникално реално число y. Числата и най-често са реални, но има и теория за комплексните логаритми.
Логаритъмът с основа 10 (b = 10) се нарича десетичен логаритъм и се използва често в науката и техниката. Натуралният логаритъм има за основа неперовото число e (b ≈ 2,71828182...) и широко се използва в математиката и физиката, заради своята проста производна. За тези две основи се използват и специални означения – ln вместо loge и lg вместо log10. Двоичният логаритъм има основа 2 (b = 2) и е често използван в компютърните науки.
Цялата част от логаритъма се нарича характеристика, а дробната част се нарича мантиса. Например има характеристика , а мантисата е .
Логаритмите започват да се използват в началото на XVII век от Джон Непер като средство за опростяване на някои изчисления. Те бързо намират широко приложение в науката и техниката за изчисления със сметачна линия или предварително подготвени логаритмични таблици. При тях се използва едно важно свойство на логаритмите – сумата от логаритмите на две числа е равна на логаритъм от тяхното произведение: loga(xy) = loga(x) + loga(y). Съвременното означение на логаритмите е въведено през XVIII век от Леонард Ойлер, който открива и тяхната връзка с експоненциалната функция.
Аналогично на логаритъма на реалните числа, комплексният логаритъм е обратна функция на експоненциалната функция при комплексните числа. Друг вариант на логаритмичната функция е дискретният логаритъм, използван в криптографията.
Логаритмичните скали се използват за по-компактно изобразяване на величини, които варират в широки граници. Например, децибелът е логаритмична мярка, измерваща отношения (електрически потенциали, мощности или звуково налягане). В химията водородният показател (pH) е логаритмична мярка за киселинността на воден разтвор. Логаритмите се срещат често в различни научни формули, както и в измервания за сложността на алгоритми и при фракталите. С тях се описват музикалните интервали, участват в оценки за броя на простите числа или в някои модели на психофизиката.
Обща информация[редактиране | редактиране на кода]
Събирането, умножението и степенуването са трите основни аритметични действия. Събирането, най-простото от тях, е обратимо чрез изваждане. Така събирането на 2 и 3 дава 5, като процесът на добавяне на 2 е обратим чрез изваждане на 2: 5 – 2 = 3. Умножението, средното по сложност действие, е обратимо чрез деление – удвояването на (умножението на с 2), е обратимо чрез деление на 2. Например, умножението е обратимо чрез делението . Смисълът на логаритмите е подобно обръщане на основно аритметично действие – повдигането на число на дадена степен, наричано степенуване. Например, повдигането на 2 на трета степен дава 8, тъй като 8 е произведението на три множителя 2:
Логаритъмът от 8 с основа 2 е 3, което изразява факта, че 2 трябва да се повдигне на трета степен, за да се получи 8. Логаритмуването е обратно действие на степенуването, което определя степенния показател, за разлика от коренуването, което също е обратно действие на степенуването, което определя основата на степента (в примера ).
Степенуване[редактиране | редактиране на кода]
Действието степенуване е ключово за разбирането на логаритмите. Повдигането на на -та степен, където е естествено число, се извършва чрез умножаването на множителя, равни на . -тата степен на се записва като , при което
Степенуването може да бъде разширено до , където е положително число, а степента е произволно реално число.[3] Например, е реципрочната стойност на . Повдигането на на степен 1/2 дава квадратен корен от . По-общо, повдигането на на рационална степен , където и са цели числа, се получава от -тия корен на
- .
Накрая, всяко ирационално число може да се апроксимира с произволна точност с рационално число. Това може да се използва за изчисляването на -тата степен на : например , а може да се изчисли с нарастваща точност чрез .
Определение[редактиране | редактиране на кода]
Логаритъмът на положително реално число при основа е степента, на която трябва да се повдигне , за да се получи . С други думи, логаритъмът на при основа е решението на уравнението [4]
- .
Логаритъмът се изписва като „“ (произнасяно като „логаритъм от при основа “).
В уравнението стойността е отговорът на въпроса „На коя степен трябва да се повдигне , за да се получи ?“.
Примери[редактиране | редактиране на кода]
- log2 16 = 4 , тъй като 24= 2×2 × 2 × 2 = 16.
- Логаритмите може да са и отрицателни: , тъй като
- log10150 е приблизително 2,176, което се намира между 2 и 3, както 150 се намира между 102= 100 и 103= 1000.
- За всяка основа b, logbb = 1 и logb 1 = 0, тъй като b1= b и b0= 1.
Логаритмични тъждества[редактиране | редактиране на кода]
Няколко важни формули, понякога наричани логаритмични тъждества или логаритмични равенства, свързват логаритмите един с друг.
Произведение, частно, степен и корен[редактиране | редактиране на кода]
Логаритъмът на произведение е равен на сбора на логаритмите на множителите, а логаритъмът на частното на две числа е разликата от техните логаритми. Логаритъмът на -тата степен на дадено число е пъти логаритъма на самото число, а логаритъмът на -тия корен е равен на логаритъма на числото, разделен на . Следната таблица описва тези тъждества с примери. Всяко от тях може да се изведе чрез субституция на лявата страна в определенията за логаритъм или .
| Формула[3] | Пример | |
|---|---|---|
| Произведение | ||
| Частно | ||
| Степен | ||
| Корен |
Смяна на основата[редактиране | редактиране на кода]
Логаритъмът logbx може да се получи от логаритмите на и при произволна основа чрез следната формула:[3]
Изхождайки от дефиниционното равенство
може да се приложи logk върху двете страни на уравнението и се получава
- .
Решавайки за се получава:
- ,
което показва, че преходният коефициент от дадена -стойност към нейната съответна -стойност е
Повечето научни калкулатори могат да изчисляват логаритми с основа 10 и .[5] Логаритмите с произволна основа могат да се изчислят с някой от тези два логаритъма въз основа на горната формула:
При дадено число и неговия логаритъм logbx при неизвестна основа , основата се получава от израза
- което се вижда от повдигането на дефиниционното равенство на степен
Конкретни основи[редактиране | редактиране на кода]
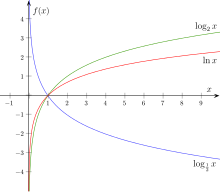
Измежду всички възможни основи на логаритмите три се използват особено често – това са b = 10, b = e (ирационалната математическа константа ≈ 2,71828) и b = 2. Логаритъмът с основа (натурален или естествен логаритъм) се използва широко в математическия анализ, заради неговите особени аналитични свойства. В същото време логаритмите с основа 10 (десетичен логаритъм) са лесни за използване при ръчни изчисления в обичайната десетична бройна система:[6]
Така log10x е свързан с броя цифри на дадено положително цяло число : броят на цифрите е най-малкото число, по-голямо от log10x.[7] Например, log101430 е приблизително 3,15, следващото цяло число е 4, което е и броят на цифрите в 1430.
Както естественият логаритъм, така и логаритъмът с основа 2 (двоичен логаритъм), се използват в информатиката, съответно в базовите единици за информация нат и бит.[8] Двоичните логаритми имат приложение и в компютърните науки, където двоичната бройна система заема централно място, във фотографията за измерване на експозиционното число,[9] както и в теорията на музиката, където важна роля има удвояването на височините (октава), а интервалите в класическата музика обикновено се измерват чрез двоични логаритми.
Следващата таблица изброява обичайните обозначения на логаритмите с тези три основи и областите, в които те се използват. В много области се изписва logx вместо logbx, когато използвана основа може да бъде определена от контекста. Понякога се среща и означението blogx.[10] Колоната „Обозначение по ISO“ показва обозначенията, препоръчвани от Международната организация по стандартизация в стандарта ISO 31-11.[11] Тъй като изписването log x се използва и за трите основи (или когато основата е неопределена или без значение), предполагаемата основа често се определя въз основа на контекста или съответната научна област. В компютърните науки и математиката log обикновено се отнася съответно за log2 и loge.[12] В други контексти log често обозначава log10.[13]
| Основа b | Наименование на logbx | Обозначение по ISO | Други обозначения | Приложение |
|---|---|---|---|---|
| 2 | двоичен логаритъм | lb x[14] | ld x, log2x, log x, lg x [15] |
компютърни науки, информатика, теория на музиката, фотография |
| e | натурален логаритъм | ln x | log x [16] | математика, физика, химия, статистика, икономика, информатика и техника |
| 10 | десетичен логаритъм | lg x | log10x, log x | техника, логаритмични таблици, спектроскопия |
История[редактиране | редактиране на кода]
Първите изследвания върху концепции сходни с логаритъма, са правени от индийския математик от VIII век Вирасена, който разглежда идеята за ардхакчеда – колко пъти число от вида 2n може да бъде разделено на две цели половини. За точните степени на 2 това число е логаритъмът за тази основа, който е цяло число. Вирасена описва и други свързани зависимости и въвежда също логаритми с основа 3 и 4.[17][18] През 1544 година германецът Михаел Щифел публикува „Обща аритметика“ („Arithmetica integra“), която съдържа таблица със степените на 2, смятана за ранен предшественик на логаритмичните таблици.[19][20][21]
Логаритмите са „изобретени“ от Джон Непер (1550 – 1617) – шотландски математик, лорд на Мърчистън, и от Йост Бюрги – приятел на Кеплер и кралски придворен часовникар в Прага, както и майстор на астрономически инструменти. Непер изобретява логаритмите преди 1594 г., но публикува откритието си едва след 20 години. В заглавието на труда му „Описание на чудната таблица на логаритмите“ („Mirifici Logarithmorum Canonis Descriptio“) личи същият възторг, с който логаритмите са били посрещани навсякъде.
Логаритмите с основа е са въведени от лондонския учител по математика Джон Спийдъл; през 1619 г. той издава таблица на „новите логаритми“ на числата от 1 до 1000. Тези логаритми възникват „естествено“ при определяне на лицата, ограничени от хиперболата у=1/х (Лицето на фигурата, ограничено от хиперболата 1/x и правите x=a и x=b, при a<b, e ln b – ln a); затова Николаус Меркатор нарича логаритмите при основа e „естествени“ или „хиперболични“. Италианският математик Пиетро Менголи също отбелязва важността на логаритмите с основа e и ги нарича Logarithmi naturali (натурални логаритми).
Термините „логаритъм“ и „антилогаритъм“, въведени от Непер, получават днешния си смисъл у Джон Уолис (1693). Непер разбира под логаритъм log sin α, а под антилогаритъм log cos α. Понятието характеристика, както и самият термин се появяват първоначално в „Arithmetica logarithmica“ на Хенри Бригс през 1624 г.; в таблиците на Непер както числата, така и техните логаритми са цели. Записването на знака над характеристиката започва от Уилям Отред в изданието на „Clavis mathematicae“ (1652), но не получава веднага признание. Мантисата (от етруското mantisa – „добавка“, „придатък“) е въведена от Уолис, който нарича така дробната част на произволна десетична дроб. За първи път Ойлер използва тази дума за означаване на десетичните знаци само на логаритъма (1748).
Думата „основа“ е заимствана от теорията на степенуването и е пренесена в теорията на логаритмите от Ойлер. Модулът на прехода е използван още от Меркатор, а терминът е въведен от Роджър Коутс (1712). Глаголът „логаритмувам“ се появява едва през XIX век.
Непер не използва никакви символи за означаване на логаритмите. Утвърждаващите се съкращения Log, log или l (у Кеплер, Бригс и Отред съответно през 1624, 1631 и 1647 г.) са се употребявали около столетие без строгото им различаване. Коши пръв предлага да се въведат различни знаци за десетичните и натуралните логаритми. Означения, близки до съвременните, са въведени от немския математик Алфред Прингсхайм (1893). Независимо от бързото разпространяване на логаритмите и утвърждаването им в практиката в тяхната теория остават още много неясни моменти дори за изключителните умове на онова време.
Названието, въведено от Непер, произхожда от гръцките думи λόγος и άρίθμός и означава буквално „числа на отношенията“; обяснява се с това, че логаритмите възникват при съпоставянето на членовете на две редици. Основата на неговите логаритми е близка до 1/е. Английският математик Бригс опростява таблиците на Непер и го убеждава да премине към десетична основа (1624). Тези логаритми впоследствие започват да се наричат „бригови“, „десетични“ или „обикновени“. Таблиците на Бюрги са съставени през периода 1603 – 1611 г. Предполага се, че са били публикувани след 10 години под названието „Таблици за геометричната и аритметичната прогресия заедно с подробно наставление, как да се разбират и използват при всякакви пресмятания“. Те остават незабелязани до 1856 г.
Исторически приложения[редактиране | редактиране на кода]

Опростявайки трудни изчисления, логаритмите допринасят за напредъка на науката, особено на астрономията. Те имат критично значение за напредъка на геодезията, астрономическата навигация и други области. Пиер-Симон Лаплас нарича логаритмите „възхитително изобретение, което, намалявайки до няколко дни работата за много месеци, удвоява живота на астронома и му спестява грешките и отвращението, неотделими от дългите пресмятания“.[22]
Основно пособие, което дава възможност за широко използване на логаритмите преди времето на калкулаторите и компютрите, са логаритмичните таблици.[23] Първата такава таблица се съставена от Хенри Бригс през 1617 година, веднага след въвеждането на логаритмите от Непер. Впоследствие се появяват таблици с все по-широк обхват. В тях са изброени стойностите на logbx и bx за всяко число x в даден интервал, с определена точност и при определена основа b (обикновено b = 10). Например, първата таблица на Бригс съдържа десетичните логаритми на всички цели числа в интервала 1 – 1000 с точност 14 цифри. Тъй като функцията f(x) = bx е обратната функция на logbx, тя е наричана антилогаритъм.[24] Произведението и частното на две положителни числа c и d редовно се изчисляват като сбора и разликата между техните логаритми. Произведението cd или частното c/d се получават от намирането на антилогаритъм от сбора или разликата, също чрез същата таблица:
и
За ръчни пресмятания, които изискват по-съществена точност, намирането на двата логаритъма, изчисляването на техния сбор или разлика и намирането на антилогаритъма е много по-бързо от извършването на умножението по по-ранните методи, като простаферезата, която се извежда от тригонометрични тъждества. Изчисляването на степени и корени се свежда до умножения или деления и търсения, чрез:
и
Много логаритмични таблици показват логаритмите, като дават поотделно цялата и дробната част на log10x.[25] Цялата част за 10 · x е единица плюс цялата част за x, а дробните части са еднакви. Това значително разширява обхвата на логаритмичните таблици – при таблица, включваща log10x за всички цели числа x в интервала от 1 до 1000, логаритъм от 3542 се апроксимира чрез:
- С помощта на интерполация може да се постигне и по-голяма точност.
Друго важно приложение на логаритмите е сметачната линия, двойка логаритмично разграфени скали, използвани за изчисления. Неподвижната логаритмична скала е изобретена от Едмънд Гънтър малко след въвеждането на логаритмите. Уилям Отред я усъвършенства с добавянето на втора плъзгаща се скала. На двете скали са поставени числа на разстояния, пропорционални на разликите между техните логаритми. Плъзгането на подвижната скала съответства на механично събиране на логаритми, както е показано тук:

Например, добавянето на разстоянието от 1 до 2 на долната скала към разстоянието от 1 до 3 на горвата скала дава произведението 6, което се отчита на долната скала. Сметачната линия е основно изчислително средство за инженери и учени до 70-те години на XX век, тъй като дава възможност, за сметка на точността, за по-бързи пресмятания от техниките, базирани на логаритмични таблици.[26]
Аналитични свойства[редактиране | редактиране на кода]
Логаритмична функция[редактиране | редактиране на кода]
За по-задълбоченото изследване на логаритмите е необходимо използването на концепцията за функция, правило, съпоставящо на дадено число друго число.[27] За да се дефинира логаритмичната функция трябва да се покаже, че уравнението
има решение и че това решение е единствено, при условие, че е положително и че е положително и различно от 1. Доказателството за това се основава на теоремата за средната стойност,[28] според която непрекъсната функция със стойности и има като стойност и всяко число между и . Дадена функция е непрекъсната, ако няма скокове.
Може да се покаже, че функцията f(x) = bx има това свойство. Тъй като f има произволно големи и произволно малки положителни стойности, всяко число y > 0 лежи между f(x0) и f(x1) при подходящ избор на x0 и x1. Така от теоремата за средната стойност следва, че уравнението f(x) = y има решение. Освен това, решението е единствено, тъй като функцията f е строго нарастваща (за b > 1) или строго намаляваща (за 0 < b< 1).[28]
Единственото решение x е логаритъмът на y при основа b, logby. Функцията, съпоставяща на y неговия логаритъм се нарича логаритмична функция (или често само логаритъм).
Функцията logbx се характеризира и формулата за произведение на логаритми
По-точно логаритъмът за всяка основа b > 1 е единствената нарастваща функция f от множеството на положителните реални числа в множеството на реалните числа, за която f(b) = 1 и[29]
Обратна функция[редактиране | редактиране на кода]

Според формулата за логаритъм на дадена степен за всяко число x,
Логаритъм при основа b от x-тата степен на b дава x. Обратно, за дадено положително число y, формулата
казва, че ако първо се логаритмува y, а след това основата се повдигне на степен логаритъма, се получава y. По този начин и двата възможни начина на съчетаване на логаритмуване и степенуване дават като резултат първоначалното число. Следователно логаритъмът с основа b е обратната функция на f(x) = bx.[30]
Обратните функции са тясно свързани с изходните функции. Техните графики си съответстват една на друга с промяна на координатите x и y (отражение спрямо диагоналната линия x = y), както е показано на схемата вдясно: дадена точка (t, u = bt) на графиката на f съответства на точка (u, t = logbu) на графиката на логаритъма и обратното. От това следва, че logb(x) е разходяща до безкрайност (става по-голяма от всяко дадено число), ако x нараства до безкрайност, при условие, че b е по-голямо от едно. В този случай logb(x) е растяща функция. За b < 1, logb(x) клони към минус безкрайност. Когато x наближава нула, logbx клони към минус безкрайност за b > 1 (съответно, към плюс безкрайност за b < 1).
Производна и антипроизводна[редактиране | редактиране на кода]

Аналитичните свойства на функциите се предават на техните обратни функции.[28] Така, тъй като f(x) = bx е непрекъсната и диференцируема функция, такава е и logby. Грубо казано, дадена непрекъсната функция е диференцируема, ако графиката ѝ няма остри чупки. Освен това, тъй като производната на f(x) е равна на ln(b)bx от свойствата на експоненциалната функция, от верижното правило следва, че производната на logbx се получава като:[28][31]
Това означава, че наклонът на тангентата към графиката на логаритъм с основа b в точката (x, logb(x)) е равен на 1/(x ln(b)).
Производната на ln x е 1/x, от което следва, че ln x е единствената антипроизводна на 1/x, която има стойност 0 за x =1. Точно тази много проста формула е причина функцията да бъде наречена „естествен логаритъм“. Това е и една от основните причина за важността на константата e.
Производната при обобщен функционен аргумент f(x) е
Частното вдясно се нарича логаритмична производна на f, изчисляването на f'(x) чрез производната на ln(f(x)) и известно като логаритмично диференциране.[32]
Антипроизводната на естествения логаритъм ln(x) е:[33]
Подобни формули могат да се изведат от това уравнение за антипроизводните на логаритмите с друга база, като се използва правилото за промяна на основата.[34]
Интегрално представяне на натуралния логаритъм[редактиране | редактиране на кода]

Натуралният логаритъм от t е равен на определения интеграл на 1/x dx от 1 до t:
С други думи, ln(t) се равнява на площта между оста x и графиката на функцията 1/x в интервала от x = 1 до x = t. Това следва от фундаменталната теорема на анализа и факта, че производната на ln(x) е 1/x. Дясната страна на това равенство може да служи за дефиниция на естествения логаритъм. От нея могат да се изведат формулите за логаритъм от произведение и степен.[35] Например, формулата за произведение ln(tu) = ln(t) + ln(u) се извежда като:
Равенство (1) разделя интеграла на две части, а равенство (2) е смяна на променливата (w = x/t). В долната илюстрация разделянето съответства на разделяне на площта на жълта и синя част. Разтягането вертикално на синята фигура с коефициент t и свиването ѝ със същия коефициент хоризонтално не променя нейната площ. След като се измести съответно наляво, площта отново е ограничена отгоре от графиката на функцията f(x) = 1/x. Така лявата синя фигура, която е интеграл на f(x) от t до tu е със същата площ, като дясната синя фигура, която е интеграл на същата функция от 1 до u. Това е геометрична илюстрация на равенство (2).

Формулата за степенуване ln(tr) = r ln(t) може да бъде изведена по подобен начин:
- .
Второто равенство използва смяна на променливата – w = x1/r.
Сборът на реципрочните стойности на естествените числа,
се нарича хармоничен ред и е тясно свързан с естествения логаритъм – когато n клони към безкрайност, разликата
е схождаща към число, наречено константа на Ойлер – Маскерони γ = 0,5772.... Тази зависимост се използва за анализ на поведението на алгоритми като бързо сортиране.[36]
Има и други интегрални представяния на логаритми, които са полезни за определени цели:
- .
Първото тъждество може да се провери, като се демонстрира, че при x = 1 двата израза имат еднаква стойност и еднаква производна. Второто тъждество се доказва от равенството
като след това се вмъкне трансформация на Лаплас на cos(xt) (и cos(t)).
Трансцендентност[редактиране | редактиране на кода]
Реалните числа, които не са алгебрични, се наричат трансценденти.[37] Например, π и e са трансцендентни числа, но не е. Почти всички реални числа са трансцендентни. Логаритъмът е пример за трансцендентна функция – според теоремата на Гелфонд-Шнайдер те обикновено имат трансцендентни стойности.[38]
Изчисляване[редактиране | редактиране на кода]

Логаритмите са лесни за изчисляване в някои частни случаи, като log10(1000) = 3. В по-общ вид логаритмите могат да се изчисляват чрез степенни редове или аритметично-геометрични средни стойности или да се отчитат от предварително изчислени логаритмични таблици с определена крайна точност.[39][40]
Итеративният метод на Нютон, предназначен за приблизително решаване на уравнения, също може да се използва за изчисляване на логаритми, тъй като тяхната обратна функция, експоненциалната, може да се изчислява с добра ефективност.[41] При възможност за използване само на събиране и битово изместване логаритмите могат да се изчисляват и с алгоритми от типа на CORDIC.[42] Освен това с алгоритъма за двоичния логаритъм lb(x) може да се изчисли рекурсивно чрез многократно повдигане на квадрат на x въз основа на отношението:
Редове на Тейлър[редактиране | редактиране на кода]
За всяко реално число z, за което 0 < z < 2, е вярна следната формула:[43]

Това е начин да се каже, че ln(z) може да се изчисли приблизително до все по-точна стойност чрез следните изрази:
Например, за z = 1.5 третото приближение дава 0,4167, което е с около 0,011 по-голямо от ln(1,5) = 0,405465. Този числов ред се приближава към ln(z) с произволна точност, стига броят на събираемите да е достатъчно голям – ln(z) е границата на реда, който е ред на Тейлър за естествения логаритъм при z = 1. Редът на Тейлър за ln(z) е особено полезно приближение на ln(1+z) за малки стойности на z – |z|< 1, тъй като за тях:
Например, за z = 0.1 приближението от първи ред дава ln(1.1) ≈ 0.1, което се отклонява само с 5% от точната стойност 0.0953.
Други степенни редове[редактиране | редактиране на кода]
Друг степенен ред, използван за изчисляване на логаритми, е базиран на функцията хиперболичен аркустангенс:
за всяко реално число z > 0.[43]
Този ред може да се изведе от описаните по-горе редове на Тейлър. Той има по-бърза сходимост от тях, особено за стойности на z близки до 1. Например, за z = 1.5 първите три събираеми на втория ред апроксимират с грешка около 3×10−6. Бързата сходимост за z близко до 1 може да се използва по следния начин – при грубо приближение y ≈ ln(z) и полагайки
логаритъмът на z е:
Колкото по-добро е първоначалното приближение y, толкова по-близо до 1 е A, така че неговият логаритъм да бъде изчислен ефективно. A може да се изчисли с използването на експоненциални редове, които имат бърза сходимост за неголеми стойности на y. За изчисляването на логаритми от по-големи стойности на z, те могат да се редуцират към по-малки стойности: , така че .
Сходен метод може да се използва за изчисляването на логаритми на цели числа. Полагайки в горния ред, се получава:
Ако логаритъмът на голямо число n е известен, тогава се получава бързо сходящ ред за log(n+1) със скорост на сходимост .
Аритметично-геометрично средно[редактиране | редактиране на кода]
Аритметично-геометричното средно може да се използва за точни приближения на естествения логаритъм. През 1982 година Сасаки и Канада демонстрират, че то е особено бързо за точности между 400 и 1000 десетични знака, докато редовете на Тейлър обикновено са по-бързи при по-ниска точност. В техните изследвания ln(x) се апроксимира с точност 2−p (или p точни бита) чрез следната формула, изведена от Карл Фридрих Гаус:[44][45]
Тук M(x, y) обозначава аритметично-геометричното средно на x и y. То се получава чрез последователно изчисляване на средното аритметично и средното геометрично на x и y, след което тези две стойности се използват като следващи x и y. Двете числа бързо се свеждат до обща граница, която е и стойността на M(x, y). m се избира така, че:
за да се осигури желаната точност. По-голямо m увеличава итерациите за изчисляване на M(x, y) (началните x и y са по-отдалечени, така че са нужни повече итерации до достигане на сходимост), но дава по-голяма точност. Константите pi и ln(2) могат да се изчислят с бързо сходящи редове.
Алгоритъм на Файнман[редактиране | редактиране на кода]
При работата си върху Проекта „Манхатън“ Ричард Файнман разработва побитов алгоритъм, подобен на дълго деление. Той използва факта, че всяко реално число може да се представи като произведение на множители от вида . Алгоритъмът последователно изгражда произведението : ако , се прави замяна на с . Това се повтаря за всяка целочислена стойност на , докато се получи желаната точност. Тъй като е сборът от събираемите от вида , съответстващи на тези , за които множителят е включен в произведението , може да се изчисли само чрез събиране, като се използва таблица за за всяко . Таблицата може да се създаде за произволна стойност на основата на логаритъма.[46]
Приложения[редактиране | редактиране на кода]

Логаритмите имат множество приложения, както в математиката, така и извън нея. Част от тях са свързани с концепцията за мащабна инвариантност. Например, в черупката на наутилусите всеки сегмент е приблизително копие на предишния, но увеличен с постоянен коефициент, дефинирайки логаритмична спирала.[47] Законът на Бенфорд за разпределението на първата цифра също може да се обясни с мащабна инвариантност.[48] Логаритмите са свързани и със самоподобието. Например, те се използват в анализа на алгоритми, които решават задачи, разделяйки ги на две сходни по-малки задачи и заместващи техните решения.[49] Размерите на самоподобни геометрични фигури, такива, чиято форма наподобява по-голяма фигура, също се базират на логаритми. Логаритмичните скали са полезни за изобразяването на относителни изменения на величини, за разлика от абсолютните им изменения. Освен това, тъй като логаритмичната функция log(x) нараства много бавно за големи стойности на x, логаритмичните скали се използват и за по-компактно представяне на стойности с големи разлики. Логаритми се използват и в множество формули в естествените науки, като формулата на Циолковски, уравнението на Фенске или уравнението на Нернст.
Логаритмична скала[редактиране | редактиране на кода]

Някои величини в науката се представят удобно като логаритми на други величини чрез използването на логаритмична скала. Например, децибелът е единица, свързана с величини в логаритмична скала. Той се базира на десетичен логаритъм от съотношения – 10 пъти десетичния логаритъм на съотношението на мощности или 20 пъти десетичния логаритъм на съотношението на електрически напрежения. Използва се за количествена оценка на загубата на напрежение при предаването на електрични сигнали,[50] за изразяване на нива на звукова мощност в акустиката,[51] за описване на поглъщането на светлина в спектрометрията и оптиката. Отношението сигнал към шум, описващо количеството нежелан шум, отнесено към смисления сигнал, също се измерва в децибели.[52] По подобен начин върховото отношение сигнал към шум често се използва за оценка на качеството на звука и компресията на изображения.[53]
Ефектите от земетресенията също се измерват удобно чрез десетичния логаритъм от освобождаваната от тях енергия. Този принцип използват скалата на моментния магнитуд и скалата на Рихтер. Например, земетресение с магнитуд 5,0 освобождава 32 пъти (101.5), а с магнитуд 6,0 – 1000 пъти (103) по-голяма енергия от земетресение с магнитуд 4,0.[54] Друга логаритмична скала е тази на видимата звездна величина, която измерва логаритмично яркостта на звездите.[55] Друг пример е водородният показател pH в химията – той е отрицателен десетичен логаритъм на активността на водородните йони H+
.[56] Разлика във водородния показател от единица съответства на десеткратна разлика в активността на водородните йони – оцет с pH около 3 е с 1000 пъти по-голяма активност на водородните йони от водата с pH = 7.
Полулогаритмичните диаграми използват идеята за логаритмичната скала за целите на визуализацията – едната ос, обикновено вертикалната, е в логаритмичен мащаб. Например, диаграмата в дясно свива рязкото нарастване от 1 милион до 1 трилион в същото разстояние по вертикалната ос, както нарастването от 1 до 1 милион. В такива диаграми експоненциалната функция от вида f(x) = a · bx изглежда като права с наклон, равен на логаритъма от b. При логаритмичните диаграми и двете оси са в логаритмичен мащаб, при което функции от вида f(x) = a · xk се изобразяват като прави с наклон, равен на експонентата k. Такива диаграми се използват за визуализацията и анализа на степенни закони.[57]
Психология[редактиране | редактиране на кода]
Логаритмите присъстват в няколко закона, описващи човешките възприятия:[58][59] законът на Хик задава логаритмично отношение между времето, за което хората правят избор, и броя на възможните избори които имат.[60] Законът на Фитс предвижда, че времето, необходимо за бързо придвижване до определено място, е логаритмична функция на съотношението между разстоянието до него и неговия размер.[61] В психофизиката законът на Вебер-Фехнер описва логаритмична зависимост между дразнител и усещане, например между действителното и възприеманото тегло на пренасян предмет,[62] макар че тази зависимост е оспорвана от по-нови модели, като закона на Стивънс.[63]
Психологически изследвания установяват, че хора с ограничена математическа подготовка са склонни да оценяват количествата логаритмично – те позиционират дадено число на немаркирана линия според неговия логаритъм, така че 10 е също толкова близо до 100, колкото 100 до 1000. По-доброто образование измества това възприемане към линейното (поставяйки 1000 10 пъти по-далече от 100, отколкото 10 при някои обстоятелства, но логаритмите продължават да се използват, когато числата са трудни за линейно изобразяване.[64][65]
Теория на вероятностите и статистика[редактиране | редактиране на кода]


Логаритмите се използват широко в теорията на вероятностите. От закона за големите числа следва, че при простия експеримент с хвърляне на монета, докато броят на хвърляния на монетата нараства към безкрайност, наблюдаваният брой на двата възможни резултата клони към равенство. Флуктуациите на всеки от двата резултата спрямо 1/2 се описват от закона за повторния логаритъм.[66]
Логаритми се използват и в логнормалното разпределение. Когато логаритъмът на дадена случайна величина има нормално разпределение, променливата има логнормално разпределение.[67] Логнормални разпределения се срещат в много области, в които величини се получават като произведение на множество независими положителни случайно величини, например при изследването на турбуленцията.[68]
Логаритми се използват в оценката за максимално правдоподобие на параметрични статистически модели. За такива модели функцията на правдоподобие зависи от поне един параметър, който трябва да бъде оценен. Максимум на функцията на правдоподобие се достига при същата стойност на параметъра, при която се достига максимум на логаритъма на правдоподобие, защото логаритъмът е монотонно растяща функция. Логаритъмъ е по-лесен за максимизиране, особено при умножавани правдоподобия на независими случайни величини.[69]
Законът на Бенфорд описва присъствието на цифрите в различни набори от данни, от рода на височини на сгради. Според него вероятността първата десетична цифра в елемент на извадката да е d (от 1 до 9) е равна на log10 (d + 1) − log10 (d), независимо от мерните единици.[70] Така може да се очаква, че 30% от стойностите започват с цифрата 1, 18% с 2 и т.н. Законът намира различни приложения, например одитори използват отклоненията от него, за да откриват възможни счетоводни измами.[71]
Изчислителна сложност[редактиране | редактиране на кода]
Анализът на алгоритми е клон на компютърните науки, който изследва ефективността на алгоритмите (обикновено компютърни програми, решаващи определена задача).[72] В него логаритмите се използват широко при описването на алгоритми, които разделят дадена задача на по-малки задачи, след което обединяват решенията на подзадачите.[73]
Например, за да намери дадено число в подреден списък, алгоритъмът за двоично търсене проверява средния елемент в списъка, след което, ако не е открил числото, продължава с половината преди или след него. Този алгоритъм изисква средно log2 (N) сравнения, където N е дължината на списъка.[74] По подобен начин алгоритъмът за подреждане чрез сливане подрежда даден неподреден списък, като го разделя на половини, които подрежда преди да слее. Алгоритмите за подреждане чрез сливане обикновено отнемат време, приблизително пропоционално на N · log(N).[75] Основата на алгоритъма не е уточнена, тъй като резултатът се променя само с константен множител при промяна на основата, което обикновено е пренебрежима разлика в анализа на алгоритми.[7]
За дадена функция f(x) се казва, че расте логаритмично, когато f(x) е точно или приблизително пропорционална на логаритъм от x.[77] Така всяко естествено число N може да бъде представено в двоична форма в не повече от log2 N + 1 бита – количеството памет, необходима за съхраняването на N нараства логаритмчино с нарастването на N.
Ентропия и хаос[редактиране | редактиране на кода]
Ентропията е обобщена мярка за неподредеността на дадена система. В статистическата термодинамика ентропията на дадена физична система се дефинира като:
където сумирането е по всички възможни състояния i на системата, например положенията на газови частици в съд, pi е вероятността за достигане на състояние i, а k е константата на Болцман. По подобен начин ентропията в теорията на информацията измерва количеството информация – ако даден получател на информация може да очаква всяко от N възможни съобщения с равна вероятност, то количеството информация, донасяна от всяко такова съобщение се оценява количествено с log2 N бита.[78]
Показателят на Ляпунов използва логаритми, за да оцени степента на хаотичност на дадена динамична система. Например, за материална точка, движеща се по овална билярдна маса, дори малки отклонения в началните условия водят до напълно различни траектории. Такива системи са хаотични по детерминистичен начин, тъй като малки грешки в измерването на началното състояние предвидимо водят до напълно различни крайни състояния.[79]
Фрактали[редактиране | редактиране на кода]

Логаритми се използват в дефиницията за размерност на фрактали.[80] Фракталите са геометрични обекти, които са самоподобни като техни части повнарят, поне приблизително, общата структура на обекта. Например, показаният на илюстрацията триъгълник на Серпински може да бъде покрит с три копия на самия себе си, но със страни намалени наполовина. Така хаусдорфовата размерност на тази структура е ln(3)/ln(2) ≈ 1.58. Друга базирана на логаритми мярка за размерността се получава чрез преброяване на клетките, необходими за покриването на даден фрактал.
Музика[редактиране | редактиране на кода]
Логаритмите са свързани с музикалните тонове и интервали. При темпериран строй съотношението между честотите зависи само от интервала между два тона, не от конкретната честота (височина) на отделните тонове. Например, нотата ла има честота 440 Hz, а си бемол е с честота 466 Hz. Интервалът между тях е един полутон, както и този между си бемол и си (честота 493 Hz). Съответно, съотношенията между честотите съвпадат:
По този начин логаритмите могат да бъдат използвани за описването на интервали – всеки интервал може да се измери в полутонове като се намери логаритъм с основа 21/12 от съотношението на честотите, докато логаритъм с основа 21/1200 изразява интервала в центове (стотни от полутона). Последната мярка се използва за по-прецизно записване, каквото се налага при нетемперираните строеве.[81]
| Интервал | 1/12 тон |
Полутон |
Терца |
Тритонус |
Октава |
| Съотношение на честотите r | |||||
| Брой полутонове |
|||||
| Брой центове |
Теория на числата[редактиране | редактиране на кода]
Естествените логаритми са тясно свързани с функцията на разпределение на простите числа, която играе важна роля в теорията на числата. За всяко цяло число x броят на простите числа, по-малки или равни на x, е равно на π(x). Според теоремата за разпределението на простите числа π(x) може да се изчисли приблизително от
като съотношението между π(x) и тази дроб клони към 1 когато x клони към безкрайност.[82] Като следствие вероятността произволно избрано число между 1 и x да е просто е обратно пропорционална на броя на десетичните цифри в x. Още по-добро приближение на π(x) се получава чрез интегралната функция Li(x), дефинирана като
Хипотезата на Риман, едно от най-старите все още отворени предположения в математика, може да се изрази чрез сравнение на π(x) и Li(x).[82] Теоремата на Ердьош-Кац, описваща броя на различните прости коефициенти, също използва естествени логаритми.
Свойството на логаритъма на n факториел, n! = 1 · 2 · ... · n
може да се използва за извеждане на формулата на Стърлинг, даваща приблизителни стойности на n! за голямо n.[83]
Обобщения[редактиране | редактиране на кода]
Комплексен логаритъм[редактиране | редактиране на кода]

Всички комплексни числа a, които са корени на уравнението
се наричат комплексни логаритми на of z за всяко комплексно число z. Комплексните числа обикновено се представят във вида z = x + iy, където x и y са реални числа, а i е имагинерна единица, квадратът на която е равен на −1. Такова число може да се визуализира като точка в комплексната равнина. Ненулевите комплексни числа могат да се представят и в полярна форма – чрез тяхната абсолютна стойност – положителното, реално разстояние от точката до началото на координатната система – и ъгъла между реалната ос x и правата, преминаваща през началото на координатната система и точката z. Този ъгъл понякога се нарича аргумент на комплексното число.
Абсолютната стойност r на z се получава от
Като се използва геометричната интерпретация на синус и косинус и тяхната периодичност на 2π всяко комплексно число z може да се опише и като
за всяко цяло число k. От това се вижда, че аргументът на z не е еднозначно определен – ако φ е валидна стойност, валидни са и стойностите φ' = φ + 2kπ за всяко цяло число k. По конвенция една от валидните стойности на аргумента – обикновено такава, която попада в един от интервалите −π < φ ≤ π[84] или 0 ≤ φ < 2π,[85] наричани клонове на аргументната функция – се избира за основен аргумент, обозначаван с Arg(z).

Формулата на Ойлер свързва тригонометричните функции синус и косинус с комплексната експонента:
Прилагайки тази формула и отчитайки периодичността на тригонометричните функции, могат да бъдат изведени следните равенства:[86]
където ln(r) е единственият реален естествен логаритъм, ak обозначава комплексните логаритми на z, а k е произволно цяло число. Следователно комплексните логаритми на z, които са всички комплексни стойности ak, за които ak-тата степен на e е равна на z, са безкрайния брой стойности
за произволна цяла стойност k.
Приемайки k, така че φ + 2kπ да бъде в дефинирания интервал на основните аргументи, получената стойност ak се нарича основна стойност на логаритъма, обозначавана с Log(z) (с главно L). Основният аргумент на всяко положително реално число x е 0; така Log(x) е реално число, което е равно на реалния (естествен) логаритъм. Въпреки това формулите за логаритмите на произведения и степени, валидни за реалните логаритми, не са приложими за основните стойности на комплексните логаритми.[87]
Обратни функции на други експоненциални функции[редактиране | редактиране на кода]
Степенуването се използва в много области на математиката, а обратните му функции често са наричани логаритми. Например, матричният логаритъм е обратната функция на матричната експонента.[88] Друг пример е p-адичният логаритъм, обратна функция на p-адичната експонента – тези две функции се дефинират чрез редове на Тейлър по аналогия с реалните им съответствия.[89] В контекста на диференциалната геометрия експоненциалното изображение преобразува допирателното пространство в дадена точка на дадено диференцируемо многообразие, изобразявайки я в околност на тази точка. Неговото обратно изображение също се нарича логаритмично.[90]
В контекста на крайните групи степенуването се дефинира като последователното умножаване на даден елемент на групата b със самия него. Дискретният логаритъм е цяло число n, което е решение на уравнението
Други сходни с логаритъма обратни функции са двойният логаритъм ln(ln(x)), суперлогаритъмът (вариант на който е наричан в информатиката итериран логаритъм), W-функцията на Ламберт и функцията логит. Те са обратните функции съответно на двойната експоненциална функция, тетрацията, f(w) = wew[92] и логистичната функция.[93]
Свързани концепции[редактиране | редактиране на кода]
От гледна точка на теорията на групите равенството log(cd) = log(c) + log(d) изразява изоморфизъм на групи между положителните реални числа, подложени на умножение, и реалните числа, подложени на събиране. Логаритмичните функции са единствените непрекъснати изоморфизми между тези групи.[94] Чрез този изоморфизъм мярката на Хаар (мярка на Лебег) dx върху реалните числа съответства на мярката на Хаар dx/x върху положителните реални числа.[95] Неотрицателните реални числа имат не само умножение, но и събиране, и образуват полупръстен, наричан вероятностен полупръстен, който е и полуполе. Така логаритъмът отнася умножението към събирането и събирането към умножението, създавайки изоморфизъм на полупръстени между вероятностния полупръстен и логаритмичния полупръстен.
Логаритмичната форма df/f, използвана в комплексния анализ и алгебричната геометрия, е диференциална форма с логаритмични полюси.[96]
Полилогаритъмът е функция, дефинирана като
Вижте също[редактиране | редактиране на кода]
Бележки[редактиране | редактиране на кода]
- ↑ Краткий словарь иностранных слов. М.: Русский язык, 1984.
- ↑ Логарифмы // Большая советская энциклопедия : [в 66 т.] / гл. ред. О. Ю. Шмидт. — 1-е изд. — М. : Советская энциклопедия, 1926—1947.
- ↑ а б в Shirali 2002.
- ↑ Kate 2009, с. 1.
- ↑ Bernstein 1999, с. 21.
- ↑ Downing 2003, с. 275.
- ↑ а б Wegener 2005, с. 20.
- ↑ Van der Lubbe 1997, с. 3.
- ↑ Allen 2011, с. 228.
- ↑ Embacher 2011.
- ↑ Taylor 1995.
- ↑ Goodrich 2002, с. 23.
- ↑ Parkhurst 2007, с. 288.
- ↑ Gullberg 1997.
- ↑ Perl 1977, с. 219 – 222.
- ↑ Rudin 1984.
- ↑ Gupta 2000, с. 329.
- ↑ Jain 1996.
- ↑ Stifelio 1544, с. 13.
- ↑ Bukhshtab 2001.
- ↑ Groza 1972, с. 182.
- ↑ Bryant 1907, с. 44.
- ↑ Campbell-Kelly 2003.
- ↑ Abramowitz 1972, с. 89.
- ↑ Spiegel 2006, с. 264.
- ↑ Maor 2009.
- ↑ Devlin 2004.
- ↑ а б в г Lang 1997.
- ↑ Dieudonné 1969, с. 84.
- ↑ Stewart 2007.
- ↑ Wolfram Alpha 2019a.
- ↑ Kline 1998, с. 386.
- ↑ Wolfram Alpha 2019b.
- ↑ Abramowitz 1972, с. 69.
- ↑ Courant 1988.
- ↑ Havil 2003.
- ↑ Nomizu 1996, с. 21.
- ↑ Baker 1975, с. 10.
- ↑ Muller 2006, с. 95.
- ↑ Hart 1968, с. 105 – 111.
- ↑ Zhang 1994, с. 281 – 292.
- ↑ Meggitt 1962, с. 210 – 226.
- ↑ а б Abramowitz 1972, с. 68.
- ↑ Sasaki 1982, с. 247 – 250.
- ↑ Ahrendt 1999, с. 302 – 312.
- ↑ Hillis 1989, с. 78.
- ↑ Maor 2009, с. 135.
- ↑ Frey 2006, с. 275.
- ↑ Ricciardi 1990, с. 21.
- ↑ Bakshi 2009, с. A5.
- ↑ Maling 2007.
- ↑ Tashev 2009, с. 98.
- ↑ Chui 1997, с. 180.
- ↑ Crauder 2008.
- ↑ Bradt 2004, с. 231.
- ↑ IUPAC 1997.
- ↑ Bird 2001.
- ↑ Goldstein 2009, с. 355 – 356.
- ↑ Matthews 2000, с. 48.
- ↑ Welford 1968, с. 61.
- ↑ Fitts 1954, с. 381 – 391.
- ↑ Banerjee 1994, с. 304.
- ↑ Nadel 2005.
- ↑ Siegler 2003, с. 237 – 243.
- ↑ Dehaene 2008, с. 1217 – 1220.
- ↑ Breiman 1992.
- ↑ Aitchison 1969.
- ↑ Mathieu 2000, с. 50.
- ↑ Rose 2002.
- ↑ Tabachnikov 2005, с. 36 – 40.
- ↑ Durtschi 2004, с. 17 – 34.
- ↑ Wegener 2005, с. 1 – 2.
- ↑ Harel 2004, с. 143.
- ↑ Knuth 1998, с. 409 – 426.
- ↑ Knuth 1998, с. 158 – 168.
- ↑ Mohr 1995, с. 298.
- ↑ В биологичните описания на растежа на организми терминът „логаритмичен растеж“ се използва по напълно различен начин, обозначавайки експоненциална функция.[76]
- ↑ Eco 1989.
- ↑ Sprott 2010.
- ↑ Helmberg 2007.
- ↑ Wright 2009.
- ↑ а б Bateman 2004.
- ↑ Slomson 1991.
- ↑ Ganguly 2005.
- ↑ Nevanlinna 2007.
- ↑ Moore 1991.
- ↑ Wilde 2006, с. 97.
- ↑ Higham 2008.
- ↑ Neukirch 1999.
- ↑ Hancock 2009, с. 379.
- ↑ Stinson 2006.
- ↑ Corless 1996, с. 329 – 359.
- ↑ Cherkassky 2007, с. 357.
- ↑ Bourbaki 1998.
- ↑ Ambartzumian 1990.
- ↑ Esnault 1992.
- ↑ Apostol 2010.
- Цитирани източници
- Abramowitz, Milton et al. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. 10th. New York, Dover Publications, 1972. ISBN 978-0486612720. (на английски)
- Ahrendt, Timm. Stacs 99 // {{{journal}}} 1564. Berlin, New York, Springer, 1999. ISBN 978-3-540-65691-3. DOI:10.1007/3-540-49116-3_28. p. 302 – 312. (на английски)
- Aitchison, J. et al. The lognormal distribution. Cambridge University Press, 1969. ISBN 978-0-521-04011-2. OCLC 301100935. (на английски)
- Allen, Elizabeth et al. The Manual of Photography. Taylor & Francis, 2011. ISBN 978-0240520377. (на английски)
- Ambartzumian, R. V. Factorization calculus and geometric probability. Cambridge University Press, 1990. ISBN 978-0-521-34535-4. (на английски)
- Apostol, T. M. Logarithm // Olver, Frank W. J. et al. NIST Handbook of Mathematical Functions. Cambridge University Press, 2010. ISBN 978-0-521-19225-5. (на английски)
- Baker, Alan. Transcendental number theory. Cambridge University Press, 1975. ISBN 978-0-521-20461-3. (на английски)
- Bakshi, U. A. Telecommunication Engineering. Pune, Technical Publications, 2009. ISBN 978-81-8431-725-1. (на английски)
- Banerjee, J.C. Encyclopaedic dictionary of psychological terms. New Delhi, M.D. Publications, 1994. ISBN 978-81-85880-28-0. OCLC 33860167. (на английски)
- Bateman, P. T. et al. Analytic number theory: an introductory course. New Jersey, World Scientific, 2004. ISBN 978-981-256-080-3. OCLC 492669517. (на английски)
- Bernstein, Stephen et al. Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability. New York, McGraw-Hill, 1999. ISBN 978-0070050235. (на английски)
- Bird, J.O. Newnes engineering mathematics pocket book. 3rd. Oxford, Newnes, 2001. ISBN 978-0-7506-4992-6. (на английски)
- Bourbaki, Nicolas. General topology. Chapters 5 – 10. Berlin, New York, Springer-Verlag, 1998. ISBN 978-3-540-64563-4. (на английски)
- Bradt, Hale. Astronomy methods: a physical approach to astronomical observations. Cambridge University Press, 2004. ISBN 978-0-521-53551-9. (на английски)
- Breiman, Leo. Probability. Philadelphia, Society for Industrial and Applied Mathematics, 1992. ISBN 978-0-89871-296-4. (на английски)
- Bryant, Walter W. A History of Astronomy. London, Methuen & Co, 1907. (на английски)
- Bukhshtab, A.A. et al. Arithmetic // Hazewinkel, Michiel. Encyclopaedia of Mathematics. Springer, 2001. ISBN 978-1556080104. (на английски)
- Campbell-Kelly, Martin. The history of mathematical tables: from Sumer to spreadsheets. Oxford University Press, 2003. ISBN 978-0198508410. (на английски)
- Cherkassky, Vladimir et al. Learning from data: concepts, theory, and methods. New York, John Wiley & Sons, 2007. ISBN 978-0-471-68182-3. (на английски)
- Chui, C. K. Wavelets: a mathematical tool for signal processing. Philadelphia, Society for Industrial and Applied Mathematics, 1997. ISBN 978-0-89871-384-8. (на английски)
- Corless, R. et al. On the Lambert W function. Т. 5. 1996. DOI:10.1007/BF02124750. Архивиран от оригинала на 2010-0-12-14. Посетен на 2011-02-13. (на английски)
- Courant, Richard. Differential and integral calculus. Vol. I. New York, John Wiley & Sons, 1988. ISBN 978-0-471-60842-4. (на английски)
- Crauder, Bruce et al. Functions and Change: A Modeling Approach to College Algebra. 4th. Boston, Cengage Learning, 2008. ISBN 978-0-547-15669-9. (на английски)
- Dehaene, Stanislas et al. Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures // Science 320 (5880). 2008. DOI:10.1126/science.1156540. p. 1217 – 1220. (на английски)
- Devlin, Keith. Sets, functions, and logic: an introduction to abstract mathematics. 3rd. Boca Raton, Fla, Chapman & Hall/CRC, 2004. ISBN 978-1-58488-449-1. (на английски)
- Dieudonné, Jean. Foundations of Modern Analysis. Т. 1. Academic Press, 1969. (на английски)
- Downing, Douglas. Algebra the Easy Way. Hauppauge, NY, Barron's, 2003. ISBN 978-0764119729. (на английски)
- Durtschi, Cindy et al. The Effective Use of Benford's Law in Detecting Fraud in Accounting Data // Journal of Forensic Accounting V. 2004. p. 17 – 34. Архивиран от оригинала на 2017-08-29. Посетен на 2018-05-28. (на английски)
- Eco, Umberto. The open work. Harvard University Press, 1989. ISBN 978-0-674-63976-8. (на английски)
- Embacher, Franz et al. Mathematisches Lexikon // mathe-online.at. mathe online: für Schule, Fachhochschule, Universität unde Selbststudium, 2011. Посетен на 22 март 2011. (на немски)
- Esnault, Hélène et al. Lectures on vanishing theorems // Birkhäuser Verlag, 1992. (на английски)
- Fitts, Paul M. The information capacity of the human motor system in controlling the amplitude of movement // Journal of Experimental Psychology 47 (6). June 1954. DOI:10.1037/h0055392. p. 381 – 391. (на английски)
- Frey, Bruce. Statistics hacks. Sebastopol, CA, O'Reilly, 2006. ISBN 978-0-596-10164-0. (на английски)
- Ganguly, S. Elements of Complex Analysis. Kolkata, Academic Publishers, 2005. ISBN 978-81-87504-86-3. (на английски)
- Goldstein, E. Bruce. Encyclopedia of Perception. Thousand Oaks, CA, Sage, 2009. ISBN 978-1-4129-4081-8. (на английски)
- Goodrich, Michael T. et al. Algorithm Design: Foundations, Analysis, and Internet Examples. John Wiley & Sons, 2002. (на английски)
- Groza, Vivian Shaw et al. Precalculus mathematics. New York, Holt, Rinehart and Winston, 1972. ISBN 978-0-03-077670-0. p. 182. (на английски)
- Gullberg, Jan. Mathematics: from the birth of numbers. New York, W. W. Norton & Co, 1997. ISBN 978-0393040029. (на английски)
- Gupta, R. C. History of Mathematics in India // Hoiberg, Dale et al. Students' Britannica India: Select essays. New Delhi, Popular Prakashan, 2000. ISBN 9780852297629. (на английски)
- Hancock, Edwin R. et al. Mathematics of Surfaces XIII: 13th IMA International Conference York, UK, September 7 – 9, 2009 Proceedings. Springer, 2009. ISBN 978-3-642-03595-1. p. 379. (на английски)
- Harel, David. Algorithmics: the spirit of computing. New York, Addison-Wesley, 2004. ISBN 978-0-321-11784-7. (на английски)
- Hart et al. Computer Approximations. New York, John Wiley, 1968. (на английски)
- Havil, Julian. Gamma: Exploring Euler's Constant. Princeton University Press, 2003. ISBN 978-0-691-09983-5. (на английски)
- Helmberg, Gilbert. Getting acquainted with fractals. Berlin, New York, Walter de Gruyter, 2007. ISBN 978-3-11-019092-2. (на английски)
- Higham, Nicholas. Functions of Matrices. Theory and Computation. Philadelphia, PA, Society for Industrial and Applied Mathematics, 2008. ISBN 978-0-89871-646-7. (на английски)
- Hillis, Danny. Richard Feynman and The Connection Machine // Physics Today 42 (2). 15 January 1989. DOI:10.1063/1.881196. p. 78. (на английски)
- IUPAC. Compendium of Chemical Terminology („Gold Book“). 2nd. Oxford, Blackwell Scientific Publications, 1997. ISBN 978-0-9678550-9-7. DOI:10.1351/goldbook. (на английски)
- Jain, Hiralal. The Shatkhandagama of Pushpadanta and Bhootabal // jainworld.com. Jain Samskriti Samrakshaka Sangha, 1996. Архивиран от оригинала на 2011-05-11. Посетен на 7 юни 2011. (на английски)
- Kate, S.K. et al. Basics Of Mathematics. Pune, Technical Publications, 2009. ISBN 978-8184317558. Архивиран от оригинала на 2020-08-05. (на английски)[неработеща препратка]
- Kline, Morris. Calculus: an intuitive and physical approach. New York, Dover Publications, 1998. ISBN 978-0-486-40453-0. (на английски)
- Knuth, Donald. The Art of Computer Programming. Reading, MA, Addison-Wesley, 1998. ISBN 978-0-201-89685-5. (на английски)
- Lang, Serge. Undergraduate analysis. 2nd. Berlin, New York, Springer-Verlag, 1997. ISBN 978-0-387-94841-6. DOI:10.1007/978-1-4757-2698-5. (на английски)
- Maling, George C. Springer handbook of acoustics. Berlin, New York, Springer-Verlag, 2007. ISBN 978-0-387-30446-5. (на английски)
- Maor, Eli. E: The Story of a Number. Princeton University Press, 2009. ISBN 978-0-691-14134-3. (на английски)
- Mathieu, Jean et al. An introduction to turbulent flow. Cambridge University Press, 2000. ISBN 978-0-521-77538-0. (на английски)
- Matthews, Gerald. Human performance: cognition, stress, and individual differences. Hove, Psychology Press, 2000. ISBN 978-0-415-04406-6. (на английски)
- Meggitt, J. E. Pseudo Division and Pseudo Multiplication Processes // IBM Journal of Research and Development 6 (2). April 1962. DOI:10.1147/rd.62.0210. p. 210 – 226. (на английски)
- Mohr, Hans et al. Plant physiology. Berlin, New York, Springer-Verlag, 1995. ISBN 978-3-540-58016-4. (на английски)
- Moore, Theral Orvis et al. Complex analysis. Singapore, World Scientific, 1991. ISBN 978-981-02-0246-0. (на английски)
- Muller, Jean-Michel. Elementary functions. 2nd. Boston, MA, Birkhäuser Boston, 2006. ISBN 978-0-8176-4372-0. (на английски)
- Nadel, Lynn. Encyclopedia of cognitive science. New York, John Wiley & Sons, 2005. ISBN 978-0-470-01619-0.
- Neukirch, Jürgen. Algebraische Zahlentheorie. Т. 322. Berlin, Springer-Verlag, 1999. ISBN 978-3-540-65399-8. (на немски)
- Nevanlinna, Rolf Herman et al. Introduction to complex analysis. Providence, RI, AMS Bookstore, 2007. ISBN 978-0-8218-4399-4. (на английски)
- Nomizu, Katsumi. Selected papers on number theory and algebraic geometry. Т. 172. Providence, RI, AMS Bookstore, 1996. ISBN 978-0-8218-0445-2. (на английски)
- Parkhurst, David F. Introduction to Applied Mathematics for Environmental Science. illustrated. Springer Science & Business Media, 2007. ISBN 978-0387342283. (на английски)
- Perl, Yehoshua et al. Understanding the complexity of interpolation search // Information Processing Letters 6 (6). December 1977. DOI:10.1016/0020-0190(77)90072-2. p. 219 – 222. (на английски)
- Ricciardi, Luigi M. Lectures in applied mathematics and informatics. Manchester, Manchester University Press, 1990. ISBN 978-0-7190-2671-3. (на английски)
- Rose, Colin et al. Mathematical statistics with Mathematica. Berlin, New York, Springer-Verlag, 2002. ISBN 978-0-387-95234-5. (на английски)
- Rudin, Walter. Principles of mathematical analysis. 3rd ed., International student. Auckland, McGraw-Hill International, 1984. ISBN 978-0070856134. (на английски)
- Sasaki, T. et al. Practically fast multiple-precision evaluation of log(x) // Journal of Information Processing 5 (4). 1982. p. 247 – 250. Посетен на 2011-03-30. (на английски)
- Shirali, Shailesh. A Primer on Logarithms. Hyderabad, Universities Press, 2002. ISBN 978-8173714146. (на английски)
- Siegler, Robert S. et al. The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity // Psychological Science 14 (3). 2003. DOI:10.1111/1467-9280.02438. p. 237 – 243. Архивиран от оригинала на 2011-05-17. Посетен на 2011-01-07. (на английски)
- Slomson, Alan B. An introduction to combinatorics. London, CRC Press, 1991. ISBN 978-0-412-35370-3. (на английски)
- Spiegel, Murray R. et al. Schaum's outline of college algebra. New York, McGraw-Hill, 2006. ISBN 978-0071452274. (на английски)
- Sprott, Julien Clinton (ed.). Elegant Chaos: Algebraically Simple Chaotic Flows. New Jersey, World Scientific Publishing, 2010. ISBN 978-981-283-881-0. (на английски)
- Stewart, James. Single Variable Calculus: Early Transcendentals. Belmont, Thomson Brooks/Cole, 2007. ISBN 978-0-495-01169-9. (на английски)
- Stifelio, Michaele. Arithmetica Integra. London, Iohan Petreium, 1544. с. 13. (на латински)
- Stinson, Douglas Robert. Cryptography: Theory and Practice. 3rd. London, CRC Press, 2006. ISBN 978-1-58488-508-5. (на английски)
- Tabachnikov, Serge. Geometry and Billiards. Providence, RI, American Mathematical Society, 2005. ISBN 978-0-8218-3919-5. p. 36 – 40. (на английски)
- Tashev, Ivan Jelev. Sound Capture and Processing: Practical Approaches. New York, John Wiley & Sons, 2009. ISBN 978-0-470-31983-3. (на английски)
- Taylor, B. N. Guide for the Use of the International System of Units (SI) // US Department of Commerce, 1995. (на английски)
- Van der Lubbe, Jan C. A. Information Theory. Cambridge University Press, 1997. ISBN 978-0521467605. (на английски)
- Wegener, Ingo. Complexity theory: exploring the limits of efficient algorithms. Berlin, New York, Springer-Verlag, 2005. ISBN 978-3540210450. (на английски)
- Welford, A. T. Fundamentals of skill. London, Methuen, 1968. ISBN 978-0-416-03000-6. OCLC 219156. (на английски)
- Wilde, Ivan Francis. Lecture notes on complex analysis. London, Imperial College Press, 2006. ISBN 978-1-86094-642-4. (на английски)
- d/dx(Log(b,x)) // wolframalpha.com. Wolfram Alpha, 2019a. Посетен на 2019-05-14. (на английски)
- Integrate(ln(x)) // wolframalpha.com. Wolfram Alpha, 2019b. Посетен на 2019-05-14. (на английски)
- Wright, David. Mathematics and music. Providence, RI, AMS Bookstore, 2009. ISBN 978-0-8218-4873-9. (на английски)
- Zhang, M et al. Table driven Newton scheme for high precision logarithm generation // IEE Proceedings – Computers and Digital Techniques 141 (5). 1994. DOI:10.1049/ip-cdt:19941268. p. 281 – 292. (на английски)
|
















![{\displaystyle {\sqrt[{3}]{8}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f378331b0d609846c021c1a0bbff0a4fc1755c3)









![{\displaystyle b^{p/q}={\sqrt[{q}]{b^{p}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f33674265c05cede1a524e580d03fa2167b9d62b)
















![{\displaystyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}x}{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85de3061851d6fb9347dc78ffcaed1775391138e)















![{\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=b^{{\frac {1}{d}}\log _{b}c}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ebc41b94e21c40782651c2b29d8aa98fcfb7814a)
















![{\displaystyle \ln(x)=\int _{0}^{\infty }\,{\frac {dt}{t}}\,\left[\cos(t)-\cos(xt)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04db45b4ecd25804e71f496f88ae498384dbf0f0)



























![{\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55acf246da64ba711e1717eb43ad81792220ab32)


![{\displaystyle {\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76610ca7878ea438fa73bd50ac4df1fecce09b9f)


![{\displaystyle \log _{\sqrt[{12}]{2}}(r)=12\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/173477b6bc89e2396abacc83ca5015ac01b0747b)





![{\displaystyle \log _{\sqrt[{1200}]{2}}(r)=1200\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1ccc3b05bf5ae0d41f85c50ab1a7ceec4e95713)















