Перпендикуляр
За информацията в тази статия или раздел не са посочени източници. Въпросната информация може да е непълна, неточна или изцяло невярна. Имайте предвид, че това може да стане причина за изтриването на цялата статия или раздел. |
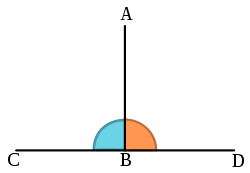
- Вижте пояснителната страница за други значения на Перпендикуляр.
В геометрията две прави се наричат перпендикулярни, ако едната образува с другата два равни съседни ъгъла. Аналогично би било да наречем едната перпендикуляр към другата. Точката, в която тази права пресича другата, се нарича пета на перпендикуляра. Следователно на Фигура 1 правата AB е както перпендикуляр към CD през точка B, така и перпендикулярна на CD през точка B.
Ако две прави са перпендикулярни, двата равни ъгъла, които сеполучават, се наричат "прави ъгли". Тяхната големина е равна на 90°, 100 града или rad.
За сравнение вж. успоредност.
Аналитично представяне
[редактиране | редактиране на кода]Чрез наклон
[редактиране | редактиране на кода]В декартова координатна система две прави е могат да бъдат описани чрез уравненията
ако никоя от тях не е перпендикулярна на оста Ox. Тогава и са наклоните на двете прави. Правите и са перпендикулярни тогава и само тогава, когато произведението на наклоните им е -1, тоест .
Чрез скаларно умножение на вектори
[редактиране | редактиране на кода]Тъй като скаларното произведение на два вектора е равно на произведението на дължините им, умножено по косинуса на ъгъла между тях, в много геометрични задачи, в които се доказва или използва перпендикулярност, е удачно да използваме векторен апарат. Тъй като cos(90°)=0, достатъчно е да докажем, че скаларното произведение на ненулевите вектори а→ и b→ е равно на нула, с което доказваме, че те са перпендикулярни. Вярно е и обратното – ако ненулевите вектори а→ и b→ са перпендикуларни, то скаларното им произведение е равно на нула, чрез което лесно и удобно могат да бъдат доказани много други твърдения.
Построяване на перпендикуляр в дадена равнина
[редактиране | редактиране на кода]
За да построим перпендикуляра към AB през P с помощта на линийка и пергел, правим следното (Фиг. 2):
- 1 (червено): построяваме окръжност K с център P и произволен радиус d. K∩AB в точките A' и B', които са равноотдалечени от P.
- 2 (зелено): Построяваме окръжности K1 и K2 с центрове съответно точките A' и B' и радиуси съответно A'Р и B'Р, следователно и двете минават през точка P. Нека Q е другата обща точка на K1 и K2.
- 3 (синьо): PQ⊥AB.
Доказателство за тази перпендикулярност намираме чрез еднаквостта на QPA' и QPB' по три равни страни, от което следва, че ъглите OPA' и OPB' са равни. След това по две равни страни и ъгъл между тях триъгълниците OPA' и OPB' са еднакви, от което следва, че ъглите POA и POB са равни.
Перпендикулярност в пространството
[редактиране | редактиране на кода]Перпендикулярност на две кръстосани прави
[редактиране | редактиране на кода]Ъгъл между две кръстосани прави и се нарича ъгълът между и 1, където 1 е права, успоредна на , минаваща през точка , лежаща върху . Две кръстосани прави се наричат перпендикулярни, ако ъгълът, който слючват, е прав.
Перпендикулярност на права и равнина
[редактиране | редактиране на кода]Правата се нарича перпендикулярна на равнината α, тогава и само тогава, когато всяка права в равнината α е перпендикулярна на . По теорема достатъчно условие за перпендикулярност между права и равнина е в равнината да съществуват две пресичащи се прави и , които са перпендикулярни на . Следователно всяка права , успоредна на , където е перпендикулярна на равнината α, също е перпендикулярна на α.
Перпендикулярност на две равнини
[редактиране | редактиране на кода]Когато две равнини се пресекат, между тях се образува двустенен ъгъл. Линейният ъгъл на един двустенен ъгъл е такъв ъгъл, чиито рамене лежат съответно в двете равнини, които се пресичат, и едновременно с това са перпенсикулярни на пресечницата на тези две равнини. Когато линейният ъгъл на двустенния ъгъл на две равнини е прав, тези равнини се наричат перпендикулярни.










