Честота

Честотата е физична величина, основна характеристика на периодичните явления, която измерва броя повторения на едно събитие за единица време. За да се изчисли честотата, може да се фиксира времеви интервал, да се преброят повтарящите се периодични събития в този интервал и след това броят им да се раздели на интервала. В електрониката и електротехниката обяснението за честота на сигнала е броят на повторенията на периода на електрическия сигнал за една секунда.
Мерни единици[редактиране | редактиране на кода]
Примери за периодични явления са въртене (например въртенето на земята около оста), трептение, вълни и други. Във физиката и инженерните дисциплини като оптика, електричество, акустика и радиоелектроника за обозначаване на честота се използва латинската буква f или гръцката ν.
В SI честотата се измерва в херци (Hz), от името на немския физик Хайнрих Херц. Честота 1 Hz означава, че даденото събитие се случва веднъж на всяка секунда. Периодът е интервалът от време, в който се повтаря дадено събитие. В SI той се означава с T и се измерва в секунди (s).
Традиционно наложила се единица в техниката и по-специално при въртящи се механични части е оборот – завъртания на минута, 60 оборота се равняват на един херц (Hz).[1]
Ъглова честота[редактиране | редактиране на кода]

Във физиката ъгловата честота ω е скаларна величина, мярка за скоростта на въртене.[2] Едно завъртане е 2π радиана, следователно[2][3]
където:
- ω е ъгловата честота или ъгловата скорост, измерена в rad/s,
- T е периодът (времето за едно завъртане), измерен в секунди,
- f е обикновената честота, измерена в Hz,
- v е тангенциалната скорост, измерена в m/s,
- r е радиусът на въртене, измерен в метри.
Звукова честота[редактиране | редактиране на кода]
Честотата на звука се определя от броя на трептенията в секунда. Измерва се с мерната единица херц (Hz) както всички други видове честоти. С увеличаването на честотата се увеличава и височината на тона. Интервалът на честотите, които човешкото ухо може да възприеме като тонове, е между 20 Hz и 20 kHz, макар че тези граници варират. Децата и младите хора чуват по-добре високите честоти. С напредване на възрастта диапазонът на чуване намалява, като способността за възприемане на високите честоти намалява значително. Честотите, към които човешкото ухо е най-чувствително, са между 1000 и 2000 Hz. Някои животни, например кучетата, могат да чуват много по-високи честоти от 20 kHz, което е границата за хората. Животните и хората са развили тези способности най-вече за да могат да комуникират помежду си. Хората могат и да записват, излъчват и предават различни видове звуци чрез различни технологии като радио, телевизия и други.
Ултразвук е звук с честота, по-висока от 20 kHz и обикновено до един милиард херца. Тези звуци са недоловими за човешкото ухо, но въпреки това могат да окажат влияние върху човека. В природата прилепите и някои видове китове издават ултразвуци.
Инфразвукът е звук с честота, по-малка от тази, доловима от човешкото ухо. За горна граница на инфразвуковите вълни се приемат честотите от 16 Hz до 20 Hz (минималната честота, която се улавя от човешкото ухо), а долната е неопределена.
В природата източници на инфразвук са електрически заряди в атмосферата, лавини, земетресения, вулкани и метеори, водопади, морски вълни, оръдейни изстрели, взривове. Известно е също така, че китовете, слоновете, носорозите, жирафите, антилопите окапи и алигаторите използват инфразвук, за да предават съобщения.
Честота в музиката[редактиране | редактиране на кода]
В музиката честотата е свързана с височината на звука. Изразява се в херци (Hz), като всяка друга честота. Честотата на звука „ла“ (440 Hz) се приема за еталон и отправна точка за другите тонове. Математически е възможно да се направят няколко изчисления, които свързват музикалните ноти и съответните им честоти.
| Честота | Нота | Музикален интервал | Изчисление на честотата |
|---|---|---|---|
| 110 | Ла1 | Октава | 440/4 |
| 220 | Ла2 | Октава | 440/2 |
| 440 | Ла3 | Октава | еталон |
| 550 | До | Терца мажор | 440 + 110 |
| 660 | Ми | Квинта | 440 + 220 |
| 990 | Си | Квинта (Ми-Си) | 660 + 330 |
Честота на електромагнитните вълни[редактиране | редактиране на кода]

Светлината е електромагнитна вълна, състояща се от трептения на електричното и магнитното полета, разпространяващи се в пространството. Различните честоти означават различен цвят на светлината. Така например червената светлина е с честота 4×1014 Hz, виолетовата – 8×1014 Hz и между тези две честоти се намират всички останали цветове от дъгата.
Една електромагнитна вълна може да има честота по-малка от 4×1014 Hz, но тогава тя е невидима за човешкото око; такива са инфрачервеното и микровълновото излъчване, и радиовълните. Една електромагнитна вълна може да има честота по-голяма от 8×1014, която също е невидима за човешкото око – това са ултравиолетовите лъчи, рентгеновите лъчи и гама лъчите.
Всички електромагнитни вълни се разпространяват във вакуум със скоростта на светлината.
От чисто удобство, по-дългите и по-бавни вълни, като например повърхностните океански и морски вълни, се описват с помощта на периода, вместо с честотата, докато при звуковите и радиовълните за предпочитане са честотите. Някои често използвани честоти са описани в таблицата:
| Честота | 1 mHz (10−3) | 1 Hz (100) | 1 kHz (103) | 1 MHz (106) | 1 GHz (109) | 1 THz (1012) |
|---|---|---|---|---|---|---|
| Период | 1 ks (103) | 1 s (100) | 1 ms (10−3) | 1 µs (10−6) | 1 ns (10−9) | 1 ps (10−12) |
Измерване и уреди[редактиране | редактиране на кода]
Броене[редактиране | редактиране на кода]
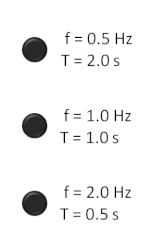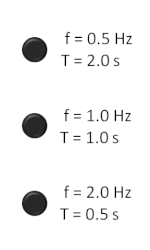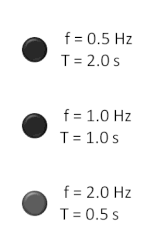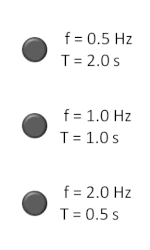
Изчисляването на честотата на повтарящо се за определен интервал от време събитие може да се осъществи, като се преброят събитията за определен период от време и след това броят се раздели на времето. Например, ако човек е на кей или на брега на море или океан и преброи 9 вълни за период от време 20 секунди, то честотата е:
Възможно е и обратното, да се отчете времето за определен брой събития и отново броят да се раздели на времето.
Стробоскоп[редактиране | редактиране на кода]
Стробоскопът е устройство, произвеждащо бързо повтарящи се светлинни импулси и позволяващо с помощта на цветовото светлинно излъчване да се наблюдават в забавен ход бързо движещи се обекти в тъмнината. Намира приложение в дискотеки и на рок концерти. Най-простата форма на стробоскоп е въртящ се диск с дупки на еднакво разстояние една от друга, който е разположен между наблюдателя и движещия се обект. Скоростта на въртене се регулира така, че да е синхронизирана с наблюдавания обект и да създава илюзията, че той се забавя и дори спира.
Честотомер[редактиране | редактиране на кода]
Уредите, с които се измерват по-високи честоти, са така наречените честотомери. Честотомерът се използва за измерване на честотата най-вече на радиосигнали, поради което е предпочитан от радиолюбители. Честотомерите могат да бъдат аналогови или цифрови, преносими или стационарни. Захранват се от батерия. Резултатът от измерването се появява на екран в Hz.
Осцилоскоп[редактиране | редактиране на кода]
В практиката често използван уред за измерване на честотата е осцилографът (осцилоскоп), с който се измерва всъщност периодът. Периодът T е обратнопропорционален на честотата (f) и се изразява чрез формулата
Той е най-разпространеният уред за наблюдаване на формата и измерването на някои параметри на периодични трептения с определена честота.
Източници[редактиране | редактиране на кода]
- ↑ Davies, A. Handbook of Condition Monitoring: Techniques and Methodology. New York, Springer, 1997. ISBN 9780412613203. с. 275.
- ↑ а б Cummings, Karen и др. Understanding physics. New Delhi, John Wiley & Sons Inc., authorized reprint to Wiley – India, Second Reprint: 2007. с. 449, 484, 485, 487.(UP1)
- ↑ Holzner, Steven. Physics for Dummies. Hoboken, New Jersey, Wiley Publishing Inc, 2006. ISBN 978-0-7645-5433-9. с. 201.
|



