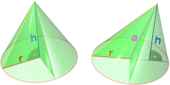
Конус

Кòнус в геометрията е геометрично тяло, заградено от конична повърхнина и едно равнинно сечение.
Конѝчната повърхнина е повърхнина, която се описва от права, минаваща през фиксирана точка O и плъзгаща се по крива ω (несъдържаща фиксираната точка), наречена управителна (директорна) крива. Правите, които минават през точка O и точките на управителната крива, се наричат образуващи на коничната повърхнина. Управителната крива не трябва да бъде изродена крива – например точка. Фиксираната точка O се нарича връх на коничната повърхнина. Ако ω е равнинна крива, върхът не бива да лежи в нейната равнина.
Конѝчно тяло е геометрично тяло, образувано от едносвързана област в дадена равнина, наречена основа, и отсечките, свързващи основата с точка извън нейната равнина, наречена връх. То е обобщение на пирамидата за немногоъгълни основи. Правите кръгови конуси също са конични тела.

Елементи на конуса[редактиране | редактиране на кода]
- Основа на конуса е част от равнина, заградена от конична повърхнина.
- Връх на конуса е върхът на коничната повърхнина.
- Образувателни или образуващи на конуса са отсечки от образуващите на коничната повърхнина от върха ѝ до основата на конуса. При прав кръгов конус всички образуващи са равни и се говори за една образувателна.
- Околна повърхнина на конуса е обединението на образуващите на конуса. При прав кръгов конус тя е част от коничната повърхнина, образувана от въртенето на единия край на образувателната на конуса по окръжност, а другият край е неподвижен във върха на конуса.
- Височина на конуса е отсечка, спусната перпендикулярно от върха към равнината на основата.
- Ъгъл на разтваряне на конуса е ъгълът между две противоположни образуващи (ъгълът при върха на конуса, вътре в конуса).
- Телесен ъгъл на конуса е пространственият ъгъл, ограничен от околната повърхнина с връх върха на конуса.
- Ос на конуса се нарича отсечката от върха на конуса до центъра на основата му. Сечението на кръгов конус с равнина през оста му се нарича осно сечение.
- Коничност (конусност) е съотношението на височината и диаметъра на основата на конуса.
- Пълната повърхнина на конуса се състои от основата и околната повърхнина.
- Обем на конуса е част от пространството, заградена от основата и околната повърхност. Обем на прав кръгов конус се нарича границата на редицата от обемите на вписаните в (или описаните около) конуса правилни пирамиди при неограничено удвояване на броя на околните им стени.



Видове конуси[редактиране | редактиране на кода]
- Прав конус е конус, чиято основа има център на симетрия (например кръг или елипса) и ортогоналната проекция на върха на конуса върху равнината на основата съвпада с този център. Оста му е перпендикулярна на основата и съвпада с височината.
- Наклонен (или кос) конус е конус, чиято ортогонална проекция на върха върху основата не съвпада с неговия център на симетрия и оста му не е перпендикулярна на основата.
- Кръгов конус е този, чиято основа е кръг.
- Прав кръгов конус се нарича кръгов конус, чиято ос е перпендикулярна на основата. Нарича се също ротационен конус, тъй като може да се получи чрез завъртане в пространството на образувателната около оста. Правият кръгов конус може да се получи и при завъртането на правоъгълен триъгълник около един от катетите му.
- Конус с основа елипса, парабола или хипербола, се нарича съответно елиптичен, параболичен и хиперболичен конус; последните два имат безкраен обем.
- Пресечен конус или коничен слой е част от конус, която лежи между основата и равнина, успоредна на основата и разположена между нея и върха.
- Равностранен конус е прав кръгов конус, чиято образувателна е равна на диаметъра на основата. [1]
-
Прав кръгов конус
(ротационен конус) -
Прав и наклонен кръгови конуси с равни основи и височини имат еднакви обеми.
-
Равностранен конус
-
Пресечен прав кръгов конус
-
Произволен конус – наклонен изпъкнало-вдлъбнат
-
Произволен конус – тройно изпъкнало-вдлъбнат
Разгънат конус[редактиране | редактиране на кода]
Правият кръгъл конус като ротационно тяло се образува от въртенето на правоъгълен триъгълник около един от катетите – височината на конуса. Вторият катет на правоъгълния триъгълник е радиусът на основата на конуса, а хипотенузата е образуващата на конуса .
В създаването на развивката на конуса се използват величините и . Радиусът определя кръга на основата на конуса. Развивката на на страничната повърхност е сектор с радиус образувателната на страничната повърхност . Секторният ъгъл в развивката на страничната повърхност на конуса се определя по формулата:

– образувателна; – секторен ъгъл; – радиус на основата.
- φ = 360°·.
Кръгов сектор[редактиране | редактиране на кода]
Кръговият сектор, получен чрез разгъване на страничната повърхност на конуса, има:
- радиус
- дължина на дъгата
- секторен ъгъл:
- в градуси
- в радиани
Повърхнина и обем на конус[редактиране | редактиране на кода]
Няма общо правило за изчисляване на повърхнината на произволно конично тяло поради неопределеният вид на управителната крива.
Обемът на всяко конично тяло е една трета от площта на основата , умножена по височината:
- .
Прав кръгов конус[редактиране | редактиране на кода]
Разглежда се прав кръгов конус с радиус на основата , височина и образувателна .
Лицето на основата се определя по формулата за лице на кръг .
Лице на околната повърхнина на прав кръгов конус се нарича границата на редицата от лицата на околните повърхнини на вписаните в него (или описаните около него) правилни пирамиди при неограничено удвояване броя на околните им стени.
След съответните математически пресмятания и граничен преход се стига до формулите за лице на околна повърхнина и пълна повърхнина :

- чрез радиуса и образувателната:
- чрез радиуса и височината:
- чрез обиколката на основата и образувателната:
- чрез ъгъла при върха и височината
Обемът на прав кръгов конус се дава с формулата
- .
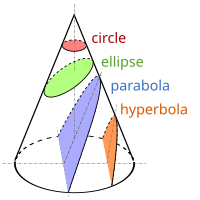
Сечения на конус[редактиране | редактиране на кода]
Сечението на произволен конус с равнина е геометрична фигура, която зависи от вида на конуса и позицията на равнината. При пресичането на прав кръгов конус с равнина в неизродени случаи сечението е кръг, елипса, парабола или хипербола, в зависимост от позицията на секущата равнина. Сечението, перпендикулярно на основата през върха на наклонен кръгов конус е триъгълник, а на прав кръгов конус – равнобедрен триъгълник.
Успоредно сечение на конус[редактиране | редактиране на кода]
Сечение на конус с равнина, успоредна на равнината на основата му, се нарича успоредно сечение на конуса. Успоредното сечение на конуса е подобна геометрична фигура на основата с по-малки размери. Всички успоредни сечения на кръгов конус са кръгове.
Важна е следната теорема: Лицето на успоредно сечение се отнася към лицето на основата като квадратът от разстоянието от това сечение до върха на конуса към квадрата от неговата височина:

- .
Пресечен кръгов конус[редактиране | редактиране на кода]
Пресечен кръгов конус се нарича тяло, което е част от кръгов конус, заключена между основата му и едно негово успоредно сечение (наричано малка основа).
Радиусът на сечението се нарича радиус на малката основа, а радиусът на основния конус – радиус на голямата основа. Отсечката от образуващата на конуса, заключена между двете основи , се нарича образувателна на пресечения конус. Разстоянието между двете основи се нарича височина на пресечения конус. Частта от околната повърхнина на дадения кръгов конус, ограничена от двете основи на пресечения конус, се нарича околна повърхнина на пресечения конус. Сумата от околната повърхнина и лицата на двете основи дава пълната повърхнина на пресечения конус.
Формулите за лице на повърхнината и обема на пресечен кръгов конус са съответно:
- Основна повърхнина:
- Околна повърхнина: ,
където е отсечената част от образувателната на конуса (образувателна на отрязания конус).
- Пълна повърхнина:
- Обем: .
За произволен пресечен конус (не непременно прав и кръгов) обемът е:
- ,
където и са съответно площите на голямата и малката основа, и са разстоянията от върха на непресечения конус съответно до голямата и малката основа на пресечения конус (или височини на непресечения и отсечения от него конус).
Свойства[редактиране | редактиране на кода]
Телесният ъгъл на прав кръгов конус е
където 2α e ъгълът при върха на конуса.
Центърът на тежестта на конично тяло се намира на разстояние 1/4 от височината, измервано от основата.
Масовият инерционен момент на конус, въртящ се около оста си зависи от масата му , радиуса на основата и плътността на конуса, определена от конструкцията му:

- плътен конус: ,
- плътен прав кръгов конус: ,
- конична обвивка:
- кух конус с много малка дебелина на стената :
- кух конус със значителна дебелина на стената :
- ,
където е вътрешният радиус на околната стена при основата. [2]
Уравнение на прав кръгов конус[редактиране | редактиране на кода]
Уравнения, определящи страничната повърхност на прав кръгъл конус с ъгъл на разтваряне 2α, връх в началото и ос, съвпадаща с оста Oz:
- В сферична координатна система с координати (r, φ, θ):
- :
- В цилиндрична координатна система с координати (r, φ, z):
- или
- В правоъгълна координатна система с координати (x, y, z):
Това уравнение в канонична форма се записва като
където константите a, с се определят от пропорцията Това показва, че страничната повърхност на прав кръгов конус е повърхност от втори ред (тя се нарича конична повърхност). В общия вид, конична повърхност от втори ред лежи върху елипса; в подходяща правоъгълна координатна система (осите Ох и Оу са успоредни на осите на елипсата, върхът на конуса съвпада с началото, центърът на елипсата лежи на оста Oz), нейното уравнение има вида
освен това a/c и b/c са равни на полуосите на елипсата. В най-общия случай, когато конусът лежи върху произволна плоска повърхност, може да се покаже, че уравнението на страничната повърхност на конуса (с върха в началото) се дава от уравнението където функцията е еднородна, т. е. удовлетворява условието за всяко реално число q.


Трансформации[редактиране | редактиране на кода]
Конусът може плавно да се трансформира в други геометрични тела и обратно чрез промяна на някой от параметрите в параметричните им уравнения.
Трансформация цилиндър – хиперболоид – двоен конус се получава чрез въртене единия край на образувателните между точки на две успоредни окръжности, а другият им край е неподвижен. Когато долният край на образувателната е под горния и тя е вертикална (t=0°), получава се цилиндрична повърхнина; когато е в противоположната точка на t=180°, се получава двоен конус. В междинните положения образувателните описват хиперболични повърхнини. Подобни модели могат да се видят в някои музеи. Уравнения на съответните повърхности: .
Еднослоен хиперболоид може да се преобразува в двоен конус чрез промяна на параметъра δ в параметричното уравнение от вида . Конусът се получава при .
Вижте също[редактиране | редактиране на кода]
Литература[редактиране | редактиране на кода]
- Георги Каменаров – Справочник Висша математика, Техника, София, 1994, ISBN 954-03-0352-4, стр. 154 – 155
- доц. кпн Д. Серафимов, Н. Николов, Г. Коларов – Справочник четиризначни математически таблици и формули, Регалия 6, София, 1994, стр. 126 – 127
- доц. Георги Петров – Дескриптивна геометрия, ДИ Техника, София 1971, стр. 197
- Станчо Димитров – Сборник задачи по Дескриптивна геометрия, Техника, София, 1969, стр. 38 – 39.
Източници[редактиране | редактиране на кода]
- ↑ Математический справочник // Архивиран от оригинала на 2020-12-02. Посетен на 2023-06-05.
- ↑ Wolfgang Demtröder: Experimentalphysik 1: Mechanik und Wärme. Gabler Wissenschaftsverlage, 2008, ISBN 978-3-540-79294-9, S. 149 ([books.google.com], abgerufen am 30 Mai 2012]).