Триъгълник
За информацията в тази статия или раздел не са посочени източници. Въпросната информация може да е непълна, неточна или изцяло невярна. Имайте предвид, че това може да стане причина за изтриването на цялата статия или раздел. |
- Вижте пояснителната страница за други значения на Триъгълник.
Триъ̀гълникът е една от основните фигури в геометрията. Представлява двуизмерна фигура, многоъгълник с три страни и три ъгъла. Може да се дефинира и като част от равнината, ограничена от три точки, нележащи на една права, и трите отсечки, съединяващи тези точки. Триъгълникът няма диагонали, защото всеки връх е съседен на другите два.

Видове триъгълници[редактиране | редактиране на кода]
В зависимост от дължините на страните си триъгълникът може да бъде:
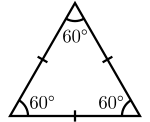
- Равностранен триъгълник – дължините на трите страни са равни; ъглите също са равни и всеки от тях е 60°.
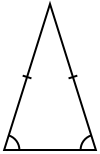
- Равнобедрен триъгълник – дължините на две от страните, наречени бедра, са равни, а третата се нарича основа; ъглите при основата са равни.
- Разностранен триъгълник – всичките му страни са с различни дължини и има три различни ъгъла.

Според големината на най-големия си вътрешен ъгъл, триъгълникът може да бъде:
- Правоъгълен триъгълник е този триъгълник, който има ъгъл от 90° (прав ъгъл). Страната, срещулежаща на правия ъгъл, се нарича хипотенуза и е най-дългата страна в правоъгълния триъгълник. Сборът от ъглите при хипотенузата е 90°. Другите две страни се наричат катети.
- Тъпоъгълен триъгълник е този триъгълник, който има вътрешен ъгъл, по-голям от 90°. Сборът на другите два ъгъла е по-малък от 90°.
- Остроъгълен триъгълник е този триъгълник, при който всички вътрешни ъгли са по-малки от 90° (остри ъгли).
 |
 |
 |
| Правоъгълен триъгълник | Тъпоъгълен триъгълник | Остроъгълен триъгълник |
Основни понятия[редактиране | редактиране на кода]
Стандартните означения в произволен триъгълник са дадени на следващия чертеж:

Основните понятия, свързани с триъгълниците, са представени от Евклид в книги 1 – 4 от „Елементите“ около 300 г. пр. н. е.
Неравенства в триъгълник[редактиране | редактиране на кода]
За страните на всеки триъгълник са изпълнени неравенствата:
- a < b + c,
- b < a + c,
- c < a + b.
Еднаквост на триъгълници[редактиране | редактиране на кода]
Два триъгълника са еднакви, ако съответните им страни и ъгли са равни. Има четири признака за еднаквост на триъгълници:
1. Ако две страни и ъгъл заключен между тях на един триъгълник са съответно равни на две страни и ъгъла заключен между тях от друг триъгълник, то триъгълниците са еднакви (по първи признак)
2. Ако два ъгъла и страна на един триъгълник са съответно равни на два ъгъла и страна на друг триъгълник, то триъгълниците са еднакви.
3. Ако трите страни на един триъгълник са съответно равни на трите страни на друг триъгълник, то триъгълниците са еднакви.
4. Ако две страни и ъгъл срещу по-голямата от тях в един триъгълник са съответно равни на две страни и ъгъл срещу по-голямата от тях в друг триъгълник, то триъгълниците са еднакви.
Съществува един често срещан частен случай на четвъртия признак:
- Ако катет и хипотенуза в триъгълник са съответно равни на катет и хипотенуза в друг триъгълник, то двата триъгълника са еднакви. (Уточнение: Третият елемент е правият ъгъл.)
Подобие на триъгълници[редактиране | редактиране на кода]
Два триъгълника са подобни, ако ъглите на единия са равни на ъглите на другия и страните, които съединяват върховете на равните ъгли, са пропорционални. Има три признака за подобни триъгълници:
1. Ако два ъгъла от един триъгълник са равни на два ъгъла от друг триъгълник, то триъгълниците са подобни.
2. Ако две страни на един триъгълник са съответно пропорционални на две страни от друг триъгълник и ъглите, заключени между тези страни, са равни, то триъгълниците са подобни.
3. Ако страните на един триъгълник са пропорционални на страните на друг триъгълник, то триъгълниците са подобни.

Точки, прави и окръжности[редактиране | редактиране на кода]
- Описана около триъгълник окръжност се нарича тази окръжност, която минава и през трите му върха.

- Симетрали в триъгълник са правите линии, които са перпендикулярни на страните и минават през средите им. Трите симетрали се пресичат в точка, която е и център на описаната около триъгълника окръжност. Диаметърът на тази окръжност може да бъде намерен, като се използва синусовата теорема, посочена по-горе.
- Теоремата на Талес гласи, че ако центърът на окръжността, описана около един триъгълник, лежи на една от страните на триъгълника, то срещуположният ъгъл на триъгълника е прав. Също така, ако центърът на описаната около триъгълника окръжност се намира във вътрешността на триъгълника, то триъгълникът е остроъгълен, а ако центърът е извън триъгълника, то триъгълникът е тъпоъгълен.

- Височини в триъгълника са перпендикулярите, спуснати от върховете на триъгълника към срещуположните страни. Трите височини на всеки триъгълник се пресичат в една точка, която се нарича ортоцентър. Ортоцентърът лежи вътре в триъгълника, само ако той не е тъпоъгълен. В противен случай ортоцентърът се намира извън триъгълника.

- Ъглополовящи в един триъгълник са тези прави, които минават през върховете на ъглите, като ги разполовяват. Пресечната точка на трите ъглополовящи е център на вписаната в триъгълника окръжност. Вписана е тази окръжност, за която страните на описания около нея триъгълник са допирателни. Триъгълниците имат и три външно вписани окръжности, които лежат извън триъгълника. Центровете на вътрешно вписаната и външно вписаните окръжности формират ортоцентричната система на триъгълника.

- Медиани в триъгълника са правите, които минават през върховете и средите на срещулежащите им страни. Трите медиани се пресичат в една точка, която се нарича медицентър на триъгълника. Медицентърът разделя всяка медиана в отношение 2:1, тоест разстоянието от върха до медицентъра е два пъти по-голямо от разстоянието от медицентъра до средата на срещулежащата страна.

- Средите на трите страни и петите на трите височините лежат върху една окръжност – окръжността на деветте точки. Останалите три точки са среди на отсечките от височините, които са заключени между върховете и ортоцентъра. Радиусът на тази окръжност е половината от радиуса на описаната около триъгълника окръжност.

- Медицентърът (в жълто), ортоцентърът (синьо), центърът на описаната окръжност (зелено) и центърът на 9-точковата окръжност (в червено) лежат на една права, известна като права на Ойлер
(червената линия). Центърът на 9-точковата окръжност е средата на отсечката, свързваща ортоцентъра и центъра на описаната окръжност. Разстоянието между медицентъра и центъра на описаната окръжност е равно на половината от разстоянието между медицентъра и ортоцентъра. Центърът на вписаната окръжност не лежи на тази права.
- Средна отсечка на триъгълник е отсечка, съединяваща средите на две от неговите страни. Нейната дължина е равна на 1/2 от дължината на срещулежащата страна на триъгълника. Средната отсечка е успоредна на срещулежащата страна.
Лице на триъгълник[редактиране | редактиране на кода]
Изчисляването на лицето на триъгълник може да стане по няколко начина:
- Геометрично:
Лицето на триъгълник е равно на полупроизведението на дължината на която и да е негова страна и височината, спусната към нея.
 |
За да се намери лицето на триъгълника (зелено), първо се прави точно негово копие (синьо), което се завърта на , и то се долепва до първия триъгълник, за да се получи успоредник. След това се отрязва излишната част и се долепва от другата страна на успоредника, за да получим правоъгълник. Тъй като лицето на правоъгълника е , то лицето на триъгълника е .
- Векторно:
 |
Лицето на успоредника може да бъде представено с помощта на векторното произведение . Понеже лицето на триъгълника е половината от това на успоредника, то .
- С помощта на тригонометрични функции:
 |
Височината на триъгълника може да бъде намерена с помощта на тригонометрията. Ако използваме означенията на чертежа вдясно, височината е . Замествайки във формулата , лицето на триъгълника може да бъде изразено като .
- С помощта на координатна система:
Нека върховете на триъгълникът са зададени с координатите си , и . Тогава лицето му може да бъде пресметнато по следния начин:
Ако върхът е в началото на координатната система, тогава:
или
Нека с бележим полупериметъра на триъгълника. Тогава:
Формулата на Херон е числово нестабилна за триъгълници с много малък ъгъл. Една стабилна алтернатива включва подреждане на дължините на страните така, че a ≥ b ≥ c и изчислението
- .
Скобите в горната формула са необходими, за да се предотврати числена нестабилност в оценката.
Синусова и косинусова теореми[редактиране | редактиране на кода]
Синусова теорема:
където е радиусът на описаната около триъгълника окръжност. Синусовата теорема може да се използва, за да бъдат намерени другите две страни на триъгълник, ако са известни една страна и два прилежащи ъгъла. Чрез нея може да се определи и сключеният ъгъл между двете известни страни, ако се знае един от другите два ъгъла.
Косинусова теорема:
В този си вид тя е валидна за всички триъгълници (не само за правоъгълните). С нея могат да бъдат намерени всички страни и ъгли в един триъгълник, ако са известни три от страните или две от тях и ъгъла, сключен помежду им.
Триъгълници в неевклидови геометрии[редактиране | редактиране на кода]
Ако всеки четири от елементите на триъгълник (върхове и/или елементи от страните му) са в една равнина един спрямо друг, триъгълникът се нарича „равнинен“. Ако триъгълникът не лежи изцяло в една равнина, то за него важат формулите на т. нар. неевклидова геометрия, а не на посочените по-горе. Например въображаем триъгълник върху земната повърхност с върхове върху екватора на 0° и 90° дължина, и Северния полюс, които вместо върху равнина са върху сфера. И трите ъгъла са прави и сборът им не е 180°. Неевклидовите геометрии изучават неравнинни триъгълници, като сферични триъгълници в сферична геометрия и хиперболични триъгълници в хиперболична геометрия.


























