Линейно пространство
Линейно пространство (или векторно пространство) в математиката е съвкупност от обекти (наричани вектори), които могат да бъдат умножавани с число или събирани. По-точно линейно пространство е множество, за което са дефинирани две операции, наричани (векторно) събиране и умножение с число, и които изпълняват няколко естествени аксиоми, описани по-долу. Линейните пространства са основният обект, с който се занимава линейната алгебра и имат широко приложение в математиката, природните и инженерните науки.
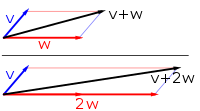
Най-познатите линейни пространства са двумерните и тримерните евклидови пространства. Векторите в тези пространства са наредени двойки или тройки от реални числа и често се представят с помощта на насочени отсечки. Тези вектори могат да бъдат събирани, използвайки правилото на успоредника, или умножавани с реални числа. Поведението им под действието на горните операции дава добър интуитивен модел за поведението на вектори в по-общи линейни пространства, които не е нужно да имат геометрична интерпретация. Например множеството на полиномите с реални коефициенти образува линейно пространство.
Формална дефиниция[редактиране | редактиране на кода]
Нека F е поле, чиито елементи ще наричаме числа или скалари (например реалните или комплексните числа). Нека също V е непразно множество, чиито елементи ще наричаме вектори. Нека във V са въведени операциите:
- събиране на вектори, която на всеки два вектора v и w съпоставя вектор, който се означава с v + w и
- умножение на вектор с число, която на вектора v и числото λ съпоставя вектор, който се означава с λv.
Казваме, че V е линейно пространство над полето F, ако за така дефинираните операции са изпълнени следните аксиоми:
- Събирането е асоциативно:
ако u, v, w ∈ V, то u + (v + w) = (u + v) + w.
- Събирането е комутативно:
ако v, w ∈ V, то v + w = w + v.
- Съществува вектор 0∈V, за който:
v + 0 = v за всеки вектор v.
Този елемент се нарича нулев вектор и може да се докаже, че е единствен. - За всеки вектор v съществува вектор w, за който е изпълнено:
За всяко v + w = 0.
w се нарича противоположен на v, отбелязва се с -v и също може да се докаже, че е единствен. - За всеки два вектора v и w и за всяко число λ е изпълнено:
λ (v + w) = λ v + λ w.
- За всеки вектор v и всеки две числа λ и μ е изпълнено:
(λ + μ) v = λ v + μ v.
- За всеки вектор v и всеки две числа λ и μ е изпълнено:
λ (μ v) = (λμ) v.
- За всеки вектор v е изплълнено:
1 v = v, където с 1 означаваме единичния елемент на F.
Формално тези аксиоми съвпадат с аксиомите за модул, така че линейно пространство може да се дефинира като модул над поле. Следователно векторните пространства са пример за модули.
Елементарни свойства[редактиране | редактиране на кода]
Следните свойства следват лесно от аксиомите за линейно пространство:
- Нулевият вектор 0 ∈ V е единствен:
Ако за 01∈ V е изпълнено 01 + v = v за всеки вектор v ∈ V, то 01 = 0.
- Резултатът от умножаване на нулевия вектор с число е нулевият вектор:
За всяко λ ∈ F имаме λ 0 = 0.
- При умножение на вектор с числото 0 се получава нулевият вектор:
За всеки v ∈ V е вярно 0 v = 0.
- В никой друг случай при умножение на вектор с число не се получава нулевият вектор:
λ v = 0 тогава и само тогава, когато λ = 0 или v = 0.
- Противоположният вектор −v на вектора v е единствен:
Ако w1 и w2 са противоположни на v, тоест v + w1 = 0 и v + w2 = 0, то w1 = w2. Противоположният вектор се означава с −v. С негова помощ се дефинира разлика на два вектора: w − v ≡ w + (−v).
- При умножение на вектор с -1 се получава противоположният му вектор:
За всеки v ∈ V е изпълнено (−1) v = −v.
- Операцията отрицание комутира:
За всяко число λ ∈ F и всеки вектор v ∈ V е изпълнено (−λ) v = λ (−v) = − (λ v).
Примери[редактиране | редактиране на кода]
Най-простият пример за линейно пространство над произволно поле е пространството, съдържащо само нулевия елемент – {0}. Също така полето F е линейно пространство над себе си – лесно се проверява, че аксиомите са изпълнени за стандартните действия събиране и умножение (например множеството на реалните числа е линейно пространство над себе си).
Един от най-важните примери за линейно пространство е координатното пространство, дефинирано по следния начин: Нека F е поле, а n е естествено число. Множеството от наредените n-торки числа от F образува линейно пространство и се отбелязва с Fn, ако дефинираме операциите събиране и умножение с число по следния начин: Нека
са елементи на Fn, където xi и yi са числа от F. Нека още λ∈ F. Дефинираме
- ,
Тези операции изпълняват горните аксиоми, като нулевият елемент е
а противоположният на x е
- .
Най-голямо приложение намират реалното координтатно пространство Rn (особено R2 и R3) и комплексното координтатно пространство Cn.
Друг пример е множеството на всички полиноми на една променлива с реални коефициенти. Там събирането и умножението по число са дефинирани по стандартния начин, а нулевият елемент е полиномът P(x)≡0. Множеството на всички функции, дефинирани над фиксирано множество и приемащи стойности в множеството на реалните числа, е линейно пространство над полето на реалните числа.
Подпространство и базис[редактиране | редактиране на кода]
При дадено линейно пространство V непразно подмножество W на V се нарича линейно подпространство, ако е затворено относно операциите събиране и умножение с число (тоест сумата на два вектора от W и произведението на вектор от W с число са елементи на W). Подпространствата на V са самите линейни пространства (над същото поле). Сечението на всички подпространства, съдържащи дадено множество вектори, се нарича линейна обвивка на това множество. Ако при премахването на който и да е вектор от множество от вектори неговата линейна обвивка се променя, казваме, че векторите в това множество са линейно независими. Линейно независимо множество от вектори, чиято обвивка е цялото линейно пространство, се нарича базис. Например в R3 множеството
е линейно подпространство на R3. Множеството е линейно независимо, докато не е, защото линейната обвивка и на двете множества е множеството A. Един възможен базис на R3 е множеството .
Всички базиси на едно линейно пространство са равномощни. Ако линейното пространство има краен базис, то се нарича крайномерно, а броят на елементите в базиса се нарича размерност на пространството. Така например R3 е крайномерно пространство с размерност 3. По-общо всички координатни пространства Fn са крайномерни с размерност n. Когато базисът има безкраен брой елементи, пространството се нарича безкрайномерно. Такива например са пространствата на полиноми и функции, дефинирани по-горе. Пример за базис на пространството от полиниоми на една променлива е множеството , което е безкрайно.
Базисът дава възможност всеки вектор да се изрази чрез наредена n-орка числа, наричана координати на вектора, спрямо фиксирания базис. Например спрямо базиса , векторът има за координати числата 1, 1 и 3, защото
- .
Линейни изображения[редактиране | редактиране на кода]
Линейно изображение е изображение, между две (може и съвпадащи) линейни пространства над едно и също поле, което запазва тяхната структура. По-точно нека V и W са линейни пространства над полето F, а e функция. Казваме, че l е линейно изображение, ако за произволни вектори u, v ∈ V и произволно число λ ∈ F е изпълнено:
- и
- .
Множеството на всички линейни изображения от V в W също е линейно пространство над F. Когато са фиксирани базиси над V и W, линейните изображения могат да се изразят с помощта на матрици.
Линейно изображение, което е едновременно и биекция, се нарича линеен изоморфизъм. Ако съществува изоморфизъм между две линейни пространства, те се наричат изоморфни; от гледна точка на линейната алгебра двете пространства са еквивалентни.
Допълнителни структури[редактиране | редактиране на кода]
Често се изучават линейни пространства, които притежават допълнителни структури. Целта им обикновено е обобщаването на стандартни понятия от геометрията.
- Реално или комплексно линейно пространство с добре-дефинирано понятие дължина или с други думи норма се нарича нормирано линейно пространство.
- Нормирано линейно пространство, за което е добре дефинирано понятието ъгъл, се нарича пространство със скаларно произведение.
- Линейно пространство, което притежава топология, съвместима с дефинраните операции (тоест такава, че събирането и умножението на вектор с число да бъдат непрекъснати), се нарича топологично линейно пространство.
- Линейно пространство с билинеен оператор (тоест умножение, което на два вектора съпоставя трети) се нарича алгебра над поле'.
Вижте също[редактиране | редактиране на кода]
- Линейна алгебра
- Вектор, за вектори в равнината и пространството
Литература[редактиране | редактиране на кода]
- Пламен Сидеров. Записки по алгебра; Линейна алгебра, изд. Веди, София, 2001.
- Кирил Дочев, Димитър Димитров. Линейна алгебра, изд. Наука и Изкуство, София, 1973.
















