Уравнение на електромагнитните вълни

Лазерите се използват за визуални ефекти по време на музикални представления.

Дъгата се образува поради дисперсия на светлината.

Микровълнова печка.

Тази многообхватна радарна антена, известна още като ALTAIR (от англ.), е предназначена за засичане и проследяване на космически обекти във връзка с противоракетната отбрана.

Оптични влакна

Уравнението на електромагнитните вълни е частно диференциално уравнение от втори ред, което описва разпространението на електромагнитните вълни в материална среда или във вакуум.

Това е вълновото уравнение, написано за електрическото поле E или магнитното поле H, което в хомогенната форма има следния вид:

$\nabla ^{2}\mathbf {E} \ -\ {1 \over c^{2}}{\partial ^{2}\mathbf {E} \over \partial t^{2}}\ \ =\ \ 0$

$\nabla ^{2}\mathbf {H} \ -\ {1 \over c^{2}}{\partial ^{2}\mathbf {H} \over \partial t^{2}}\ \ =\ \ 0$

където c е скоростта на светлината в дадената материална среда. Във вакуум c = 2,998×10⁸ m/s, което е и скоростта на светлината в свободно пространство. Уравнението за електромагнитните вълни се извежда от уравненията на Максуел. В линейна, изотропна и бездисперсионна среда магнитното поле B (магнитна индукция [T]) се отнася към H (интензитет на магнитното поле A/m) като:

$\mathbf {B} =\mu \mathbf {H}$

където μ е магнитната проницаемост на средата

Скорост на разпространение

Във вакуум

Ако вълновото разпространение е във вакуум, тогава:

$c=c_{o}={1 \over {\sqrt {\mu _{o}\varepsilon _{o}}}}=2,998\times 10^{8}$ m/s

е скоростта на светлината. Магнитната проницаемост $\ \mu _{o}$ и диелектричната проницаемост $\ \varepsilon _{o}$ са важни физични константи, които играят ключова роля в теорията на електромагнитното поле.

Символ	Име	Числена Стойност	Измервателна единица SI
$c\$	Скорост на светлината	$2,998\times 10^{8}$	m/s
$\ \varepsilon _{0}$	Диелектрична константа	$8,854\times 10^{-12}$	F/m
$\ \mu _{0}\$	Магнитна проницаемост във вакуум	$4\pi \times 10^{-7}$	H/m

В материална среда

За целите на настоящата статия, се допуска, че всички материали са линейни, изотропни и бездисперсионни. В този смисъл, скоростта на светлината в материална среда е:

$c={c_{o} \over n}={1 \over {\sqrt {\mu \varepsilon }}}$

където

$n={\sqrt {\mu \varepsilon \over \mu _{o}\varepsilon _{o}}}$

е коефициент на пречупване на средата, $\mu \,$ е магнитната проницаемост на средата и $\varepsilon \,$ е диелектричната проницаемост на последната.

Произход на електромагнитното уравнение

Запазване на заряда

Запазването на заряда изисква времето за промяна на пълния заряд намиращ се в обем Vда бъде равно на пълния ток течащ през повърхността S обхващаща обема:

$\oint _{S}\mathbf {J} \cdot d\mathbf {a} =-{d \over dt}\int _{V}\rho \cdot dV$

където J е токовата плътност [A/m²] течаща през повърхнината, а ρ е плътността на заряда [C/m³] във всяка точка от обема. От теоремата за дивергенцията, тази зависимост се преобразува от интегрална в диференциална форма:

$\nabla \cdot \mathbf {J} =-{\partial \rho \over \partial t}$

Закон на Ампер преди корекцията на Максуел

В своята оригинална форма, законът на Ампер (единици SI) е зависимостта на магнитното поле H и източника на полето, токовата плътност J:

$\oint _{C}\mathbf {H} \cdot d\mathbf {l} =\int _{S}\mathbf {J} \cdot d\mathbf {a}$

Отново може да се преобразува до диференциална форма, прилагайки Теоремата на Стокс:

$\nabla \times \mathbf {H} =\mathbf {J}$

Разглеждане на Максуел

Джеймс Клерк Максуел, който обединява законите за електричеството и магнетизма, открива важно несъответствие между закона на Ампер и закона за запазване на заряда.

Ако се вземе дивергенцията от двете страни на закона на Ампер, се получава:

$\nabla \cdot (\nabla \times \mathbf {H} )=\nabla \cdot \mathbf {J}$

Дивергенцията на ротация на което и да е векторно поле –, в случая магнитното поле H – е винаги равна на нула:

$\nabla \cdot (\nabla \times \mathbf {H} )=0$

Многолентова ротационна, насочена антена, използвана за радиолюбителски цели

Комбинирайки тези две уравнения се получава:

$\nabla \cdot \mathbf {J} =0$

От закона за запазване на заряда се знае:

$\nabla \cdot \mathbf {J} =-{\partial \rho \over \partial t}$

${\partial \rho \over \partial t}=0$

Този последен резултат подсказва, че пълната плътност на заряда в която и да е точка в пространството е константа, която изобщо не може да се променя, което разбира се е абсурдно. Не само този резултат е в противоречие на физическата интуиция, той е в противоречие и с хиляди емпирични резултати от хиляди лабораторни експерименти. Тази зависимост изисква не само запазване на заряда, но и че последния не може да бъде преразпределен от едно място към друго. Но от друга страна е известно, че електрическите токове могат и преразпределят електрическия заряд. Така последният резултат е некоректен. Нещо очевидно липсва в закона на Ампер и Максуел открива, че е необходима корекция.

Андре Мари Ампер (1775 – 1836), френски физик роден в Марсилия

За да се разбере Максуеловата корекция на закона на Ампер, трябва да се разгледа друго от уравненията на Максуел, а именно законът на Гаус в интегрална форма:

$\oint _{S}\varepsilon _{o}\mathbf {E} \cdot d\mathbf {a} =\int _{V}\rho \cdot dV$

Чрез отново използване на теоремата за дивергенцията, уравнението може да се преобразува до диференциална форма:

$\nabla \cdot \varepsilon _{o}\mathbf {E} =\rho$

Чрез диференциране по времето от двете страни се получава:

${\partial \over \partial t}(\nabla \cdot \varepsilon _{o}\mathbf {E} )={\partial \rho \over \partial t}$

При смяна на местата на производните от лявата страна се получава:

$\nabla \cdot \varepsilon _{o}{\partial \mathbf {E} \over \partial t}={\partial \rho \over \partial t}$

Последният резултат заедно със закона на Ампер и уравнението за запазване на заряда, предполага два вида източници на магнитното поле: токовата плътност J, както Ампер вече е установил и така наречения ток от промяна на електрическата индукция във времето:

${\partial \mathbf {D} \over \partial t}=\varepsilon _{o}{\partial \mathbf {E} \over \partial t}$

Така коригираната от Максуел форма на закона на Ампер има вида:

$\nabla \times \mathbf {H} =\mathbf {J} +\varepsilon _{o}{\partial \mathbf {E} \over \partial t}$

Максуел открива, че светлината е електромагнитна вълна

Картичка от Максуел до Питър Таит.

Корекцията на Максуел на закона на Ампер подготвя едно сензационно за времето си откритие. Максуел осъзнава, че уравненията за електромагнетизма предполагат че електрическото и магнитно полета могат да се разпространяват в космоса – тоест, при отсъствието на материя – като електромагнитни вълни и още, че скоростта на тези вълни е точно скоростта на светлината. Уповавайки се на откритието си в 1865, Максуел пише:

Тази скорост е толкова близка до скоростта на светлината, че изглежда имаме сериозна причина да заключим, че самата светлина... е електромагнитно смущение във формата на вълни, разпространяващи се посредством електромагнитното поле и според законите за електромагнитното поле.

При получаването на електромагнитни вълни във вакуум, се записват следните Максуелови уравнения:

$\nabla \cdot \mathbf {E} =0$

$\nabla \times \mathbf {E} =-\mu _{o}{\frac {\partial \mathbf {H} }{\partial t}}$

$\nabla \cdot \mathbf {H} =0$

$\nabla \times \mathbf {H} =\varepsilon _{o}{\frac {\partial \mathbf {E} }{\partial t}}$

Ако се приложи ротация на уравненията с ротация се получава:

$\nabla \times \nabla \times \mathbf {E} =-\mu _{o}{\frac {\partial }{\partial t}}\nabla \times \mathbf {H} =-\mu _{o}\varepsilon _{o}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}}$

$\nabla \times \nabla \times \mathbf {H} =\varepsilon _{o}{\frac {\partial }{\partial t}}\nabla \times \mathbf {E} =-\mu _{o}\varepsilon _{o}{\frac {\partial ^{2}\mathbf {H} }{\partial t^{2}}}$

Ако се има предвид вектора: $\mathbf {V}$,

$\nabla \times \left(\nabla \times \mathbf {V} \right)=\nabla \left(\nabla \cdot \mathbf {V} \right)-\nabla ^{2}\mathbf {V}$

се получават вълновите уравнения

${\partial ^{2}\mathbf {E} \over \partial t^{2}}\ -\ c^{2}\cdot \nabla ^{2}\mathbf {E} \ \ =\ \ 0$

${\partial ^{2}\mathbf {H} \over \partial t^{2}}\ -\ c^{2}\cdot \nabla ^{2}\mathbf {H} \ \ =\ \ 0$

където

$c={1 \over {\sqrt {\mu _{o}\varepsilon _{o}}}}=2,998\times 10^{8}$ m/s

е скоростта на светлината във вакуум.

Нехомогенно вълново уравнение

Локализирани променливи във времето плътности на заряда и тока могат да действат като източници на електромагнитни вълни във вакуум. Уравненията на Максуел могат да бъдат написани във формата на вълново уравнение с източници. Прибавянето на източници към вълновите уравнения прави частните диференциални уравнения нехомогенни.

Система SI

Уравненията на Максуел във вакуум с източници от заряд $\rho$ и ток $\mathbf {J}$ могат да се запишат във вид на векторни и скаларни потенциали като:

$\nabla ^{2}\varphi +{{\partial } \over \partial t}\left(\nabla \cdot \mathbf {A} \right)=-{\rho \over \varepsilon _{0}}$

$\nabla ^{2}\mathbf {A} -{1 \over c^{2}}{\partial ^{2}\mathbf {A} \over \partial t^{2}}-\nabla \left({1 \over c^{2}}{{\partial \varphi } \over {\partial t}}+\nabla \cdot \mathbf {A} \right)=-\mu _{0}\mathbf {J}$

където

$\mathbf {E} =-\nabla \varphi -{\partial \mathbf {A} \over \partial t}$

и

$\mathbf {B} =\mu _{0}\mathbf {H} =\nabla \times \mathbf {A}$.

Компактна луминесцентна лампа (КЛЛ)

Ако се допусне, че е в сила уравнението на Л.Лоренц:

${1 \over c^{2}}{{\partial \varphi } \over {\partial t}}+\nabla \cdot \mathbf {A} =0$

тогава за нехомогенните вълнови уравнения се записва:

$\nabla ^{2}\varphi -{1 \over c^{2}}{\partial ^{2}\varphi \over \partial t^{2}}=-{\rho \over \varepsilon _{0}}$

$\nabla ^{2}\mathbf {A} -{1 \over c^{2}}{\partial ^{2}\mathbf {A} \over \partial t^{2}}=-\mu _{0}\mathbf {J}$.

Решения на хомогенното вълново уравнение

Общото решение на уравненивто има следната форма:

$\mathbf {E} (\mathbf {r} ,t)=g(\phi (\mathbf {r} ,t))=g(\omega t-\mathbf {k} \cdot \mathbf {r} )$

и

$\mathbf {H} (\mathbf {r} ,t)=g(\phi (\mathbf {r} ,t))=g(\omega t-\mathbf {k} \cdot \mathbf {r} )$

за всяка непрекъсната и диференцируема функция g на безразмерен аргумент φ, където

$\ \omega$ е ъгловата скорост (в rad/s), и

$\mathbf {k} =(k_{x},k_{y},k_{z})$ е вълновият вектор (в rad/m).

Въпреки че функцията g може да бъде и често е монохроматична синусоидална вълна, тя не трябва да бъде синусоидална и дори периодична. На практика g не може да има безкрайна периодичност, тъй като всяка реална електромагнитна вълна трябва да има крайно протежение в пространството и времето. Като резултат от това и базирайки се на Трансформацията на Фурие, една реална вълна трябва да се състои от наслагването (суперпозицията) на безкраен брой хармоници.

Още повече, за намиране на приемливо решение, вълновият вектор и ъгловата честота не могат да бъдат независими една от друга променливи. Те трябва да спазват дисперсионната зависимост:

$k=|\mathbf {k} |={\omega \over c}={2\pi \over \lambda }$

където k е числото на вълната и λ е дължината на вълната.

Монохроматична синусоидална стационарна вълна

Най-проста форма решения на вълновото уравнение се получават от допускането за синусоидални вълни на една честота в разделена форма:

$\mathbf {E} (\mathbf {r} ,t)=\mathrm {Re} \{\mathbf {E} (\mathbf {r} )e^{j\omega t}\}$

където

• $j={\sqrt {-1}}\,$ е имагинерната единица,
• $\omega =2\pi f\,$ е ъгловата скорост в rad/s,
• $f\,$ e честотата в Hz, и
• $e^{j\omega t}=\cos(\omega t)+j\sin(\omega t)\,$ е формулата на Ойлер.

Решения за плоски вълни

Разглежда се равнина определена от единичен нормален вектор

$\mathbf {n} ={\mathbf {k} \over k}$.

Решенията за разпространяваща се планарна вълна са

$\mathbf {E} (\mathbf {r} )=E_{0}e^{-j\mathbf {k} \cdot \mathbf {r} }$

и

$\mathbf {H} (\mathbf {r} )=H_{0}e^{-j\mathbf {k} \cdot \mathbf {r} }$

където

$\mathbf {r} =(x,y,z)$ е пространствения вектор [m].

Тези решения представят планарни вълни, разпространяващи се по посока на нормалния вектор $\mathbf {n}$.

Ако посоката z се дефинира като посока на $\mathbf {n}$ и посоката (координатната ос) x като посока на $\mathbf {E}$, тогава според закона на Фарадей магнитното поле лежи по посока на y и е свързано с електрическото поле чрез отношението:

$\mp c\mu _{o}{\partial H \over \partial z}={\partial E \over \partial z}$.

Поради факта, че дивергенцията на електрическото и магнитно полета е нула, няма полета по посоката на разпространение.

Това решение касае вълновите уравнения с линейна поляризация. В този смисъл съществуват и решения с кръгова поляризация, при която полетата се въртят около нормалния вектор.

Разлагане в спектър

Поради линейността на уравненията на Максуел във вакуум, решенията могат да се разложат в суперпозиция на хармоници. Това е принципа на използването на метода с преобразование на Фурие за решаването на диференциални уравнения. Хармоничното решение на електромагнитно-вълновото уравнение има формата:

Илюстрация на областите на електромагнитния спектър и възможни практически приложения.

$\mathbf {E} (\mathbf {r} ,t)=E_{0}\ cos(\omega t-\mathbf {k} \cdot \mathbf {r} +\phi _{0})$

и

$\mathbf {H} (\mathbf {r} ,t)=H_{0}\ cos(\omega t-\mathbf {k} \cdot \mathbf {r} +\phi _{0})$

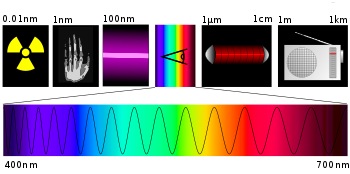
Електромагнитният спектър е диаграма на големината на интензитета на полето (или енергията на полето) във функция на дължината на вълната.