Уейвлет

Уейвлет (на английски: wavelet – „кратка вълна“) е математическа функция, която се използва за разлагането на функции или непрекъснати във времето сигнали по честотни елементи и изучаването на всеки честотен елемент с разделителна способност, съответстваща на мащаба му. Под уейвлет преобразование или уейвлет трансформация (wavelet transformation) се разбира представянето на функция чрез уейвлети. Уейвлетите са мащабирани и транслирани копия (дъщерни уейвлети) на уейвлет-майка, която обикновено е бързо затихващо трептене или такова с крайна дължина. Предимството на уейвлет преобразование пред класическото преобразуване на Фурие се проявява най-вече при представянето на функции с остри скокове, точки на прекъсване, както и за точното разлагане и възстановяване на крайни непериодични сигнали или на променливи сигнали.

Формално такова представяне се разглежда като едно разлагане на функция от L² спрямо ортонормиран базис от дъщерни уейвлети или пълна редица (рамка или Рисов базис от дъщерни уейвлети) в L².

Уейвлет преобразуванията биват дискретно (ДВП, DWT) и непрекъснато (НВП, CWT). И двете са преобразувания на непрекъснати във времето аналогови сигнали. НВП използва всички възможни мащаби и транслации, докато ДВП използва само изброимо много мащаби и транслации от предварително зададен масив.

Произход на понятието

Терминът „уейвлет“ е бил използван в продължение на десетилетия в областта на цифровата обработка на сигнали и при геофизични изследвания.^[1] Понятието уейвлет („кратка вълна“, „елементарна вълна“) е въведено от Жан Морле, (фр. Morlet) и Александар Гросман, (хърв. Grossmann) през 80-години на XX век. Те използват френската дума ondelette, която означава „вълничка“. После тя е преведена на английски като „wavelet“ със същото значение.

Теория на уейвлетите

Теорията има широко приложение в много математически и инженерни области. Всички уейвлет преобразования или уейвлет преобразувания (ВП, WT) могат да се разглеждат като друг вид времево-честотно представяне или за непрекъснати във времето (или аналогови) сигнали и се свързват с хармоничния анализ. Почти всички ДВП с практическо приложение използват дискретни във времето филтър-банки или комплекти от филтри (уейвлета и коефициентите за мащаба). Те съдържат филтри с крайна импулсна характеристика (КИХ, FIR) или филтри с безкрайна импулсна характеристика (БИХ, IIR). Уейвлетите формиращи НВП, CWT се подчиняват на съотношение на неопределеност на Хайзенберг, HUP, от теорията за вземане на извадки (sampling): разглеждайки даден сигнал, някакво събитие в него, не може да се присвои едновременно точно положение на отклика на това събитие, и по времевата, и честотната ос. Произведението на неопределеностите на отклика по време и по честота има долна граница. Така, в скалограмата на непрекъснатото уейвлет преобразование на този сигнал, такова събитие отбелязва цяла област в равнината на времевата скала, ос, вместо само една точка. Също така ДВП могат да бъдат разглеждани в контекста на други съотношения на неопределеност.

ВП се делят на три основни вида: непрекъснати, дискретни и основани на многомащабно приближение.

Непрекъснати уейвлет преобразувания (Параметри – непрекъснато отместване и мащабиране)

Даден сигнал с ограничена енергия при непрекъснати уейвлет преобразувания се проектира върху непрекъснато семейство от честотни ленти или подобни подпространства на функционално пространство L^p или функционно пространство $L^{2}(\mathbb {R} )$ . В този смисъл сигналът може да бъде представен във всяка честотна лента от тип $[f,\,2f]$ за всички положителни честоти f>0 или това е октавата в акустиката. Оттук сигналът може да бъде възстановен чрез подходящо обединяване на всички резултантни честотни компоненти. Честотните ленти или подпространства (подленти) са мащабирани варианти на подпространство с мащаб 1. Това подпространство е най-вътрешното положение като място, породено чрез отместване на дадена пораждаща (генерираща) функция $\psi \in L^{2}(\mathbb {R} )$ , уейвлети-майки. Един пример за мащабиране в единична честотна лента, или за интервала от едно до две [1,2], е тази функция

\psi (t)=2\,\operatorname {sinc} (2t)-\,\operatorname {sinc} (t)={\frac {\sin(2\pi t)-\sin(\pi t)}{\pi t}}

,

чрез нормализираната sinc функция. Известни са и множество други функции като:

.

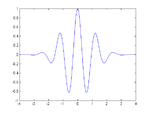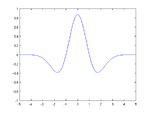Подпространството с мащаб a или честотна лента $[1/a,\,2/a]$ се генерира чрез функциите (понякога наричани дъщерни уейвлети)

\psi _{a,b}(t)={\frac {1}{\sqrt {a}}}\psi \left({\frac {t-b}{a}}\right)

,

където a е положително и определя мащаба и b е някое реално число и определя отместването. Двойката (a,b) определя една точка в дясната полуравнина $\mathbb {R} _{+}\times \mathbb {R}$ .

Така проекцията на една функция x върху подпространството с мащаб a има вида

x_{a}(t)=\int _{\mathbb {R} }WT_{\psi }\{x\}(a,b)\cdot \psi _{a,b}(t)\,db

с уейвлетни коефициенти

WT_{\psi }\{x\}(a,b)=\langle x,\psi _{a,b}\rangle =\int _{\mathbb {R} }x(t){\overline {\psi _{a,b}(t)}}\,dt

.

За анализа на сигнала x, може да се построят уейвлетните коефициенти в мащабограмата или скейлограмата на сигнала.

Дискретно уейвлет преобразуване (дискретни параметри на транслации и мащабирания)

Поради невъзможността да се прави числен анализ на даден сигнал по всички уейвлет коефициенти възниква въпросът, дали е възможно да се възстанови сигнал по съответно взетите уейвлет коефициенти, като се избират дискретни подмножества от горната полуравнина. Такава система е например афинната система за някои реални параметри a>1 и b>0. Съответното дискретно подмножество на горната полуравнина съдържа всички точки $(a^{m},n\,a^{m}b)$ с целочислени индекси $m,n\in \mathbb {Z}$ . Така за съответните породени уейвлети се получава

\psi _{m,n}(t)=a^{-m/2}\psi (a^{-m}t-nb)

.

Едно достатъчно условие за възстановяване на някакъв сигнал x с крайна енергия по формулата

x(t)=\sum _{m\in \mathbb {Z} }\sum _{n\in \mathbb {Z} }\langle x,\,\psi _{m,n}\rangle \cdot \psi _{m,n}(t)

е това функциите $\{\psi _{m,n}:m,n\in \mathbb {Z} \}$ да формират стегнат (твърд) фрейм от векторно пространство от $L^{2}(\mathbb {R} )$ .

Многомащабно дискретно уейвлет приближение

Във всяко дискретизиране на уейвлет преобразуване, за всяка ограничена правоъгълна област от горната полуравнина, се получава само ограничен брой от уейвлетни коефициенти. Нещо повече, всеки един коефициент изисква оценяване на интеграл. За да се намали изчислителната сложност, е необходима една вспомагателна функция, уейвлет-баща (father wavelet) $\phi \in L^{2}(\mathbb {R} )$ .

Освен това изисква се a да бъде цяло число. Един типичен избор е a=2 и b=1. Най-известната двойка от уейвлет-баща и уейвлет-майка е от вида уейвлет на Добеши, Добеши 4, или db4 уейвлет, по името на Ингрид Добеши.

От уейвлетите-майки и бащи могат да се построят подпространствата

V_{m}=\operatorname {span} (\phi _{m,n}:n\in \mathbb {Z} )

, където

\phi _{m,n}(t)=2^{-m/2}\phi (2^{-m}t-n)

и

W_{m}=\operatorname {span} (\psi _{m,n}:n\in \mathbb {Z} )

, където

\psi _{m,n}(t)=2^{-m/2}\psi (2^{-m}t-n)

.

От тук се изисква редицата (последователността)

\{0\}\subset \dots \subset V_{1}\subset V_{0}\subset V_{-1}\subset \dots \subset L^{2}(\mathbb {R} )

да образува едно многомащабно приближение на $a^{m}$ и подпространствата $\dots ,W_{1},W_{0},W_{-1},\dots \dots$ да са ортогонални „разлики“ от горната редица, така че, $W_{m}$ е ортогонално допълнение на $V_{m}$ вътре в подпространството $V_{m-1}$ . По аналогия с теоремата за дискретизацията може да се направи заключение, че пространството $V_{m}$ с разстояние на дисктеризация $2^{m}$ повече или по-малко покрива честотната лента от 0 до $2^{-m-1}$ . Така ортогоналното допълнение, $W_{m}$ грубо покрива лентата $[2^{-m-1},2^{-m}]$ .

От тези отношения на вложение и ортогоналност следва съществуването на редиците $h=\{h_{n}\}_{n\in \mathbb {Z} }$ и $g=\{g_{n}\}_{n\in \mathbb {Z} }$ , които удовлетворяват тъждествата:

h_{n}=\langle \phi _{0,0},\,\phi _{-1,n}\rangle

and

\phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n)

и

g_{n}=\langle \psi _{0,0},\,\phi _{-1,n}\rangle

and

\psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n)

.

Второто тъждество от първата двойка е едно мащабиращо уравнение за уейвлета-баща $\phi$ .

И двете двойки тъждества образуват основата на алгоритъма за бързо уейвлет преобразуване. Може да се отбележи, че не всеки дискретен уейвлет ортонормален базис може да бъде асоцииран към мултирезолюционния анализ; например, множеството Journe уейвлет не допуска мултирезолюционен анализ.

Уейвлети-майки

При приложения на практика и от съображения за ефективност, се предпочитат функции с компактен носител като майка (прототип) на уейвлети (функции). Все пак, за да се определят изисквания за аналитичност (при непрекъснато WT) и като цяло теоретични изисквания, се избират уейвлети от подпространството на пространство $L^{1}(\mathbb {R} )\cap L^{2}(\mathbb {R} ).$ Това е пространството от измерими функции, които са абсолютно интегрируеми и със сумируем квадрат:

\int _{-\infty }^{\infty }|\psi (t)|\,dt<\infty

and

\int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt<\infty .

Принадлежността към това пространство, означава че може да се определят условията за нулево средно и единична квадратична норма:

\int _{-\infty }^{\infty }\psi (t)\,dt=0

– условието за нулево средно, и

\int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt=1

– условието за единична квадратична норма.

\int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt=1

– условието за единична квадратична норма.

За да бъде бъде $\psi$ уейвлет за непрекъснато уейвлет преобразуване (виж там за точните условия), уейвлетът-майка трябва да удовлетворява критерий за допустимост (или най-общо казано да е от клас полу-диференцируеми), за да има твърдо (стабилно) обратно преобразуване.

За дискретното уейвлет преобразуване, трябва да е изпълнено като минимум условието, че реда от уейвлети е представяне на единица в пространство-то $L^{2}(\mathbb {R} )$ . Повечето построения на дискретни уейвлетни преобразувания използват мултирезолюционния анализ, който определя уейвлета чрез мащабиращата функция. Тази мащабираща функция е решение на функционално уравнение.

В повечето ситуации е полезно да се ограничи $\psi$ , да бъде непрекъсната функция с по-голям брой M затихващи моменти (приближаващи се до нулата), т.е. за всички числа m<M

\int _{-\infty }^{\infty }t^{m}\,\psi (t)\,dt=0.

Уейвлетът-майка е мащабирана (или дилатирана) с коефициент a и транслирана (или отместена) на коефициент b, за да се получи (според оригиналната формулировка на Морле, Morlet):

\psi _{a,b}(t)={1 \over {\sqrt {a}}}\psi \left({{t-b} \over a}\right).

За непрекъснатото WT, двойката (a,b) изменя, варира върху цялата полу-равнина R₊ × R; за дискретното WT тази двойка варира върху едно нейно дискретно подмножество, което се нарича също така афинна група. Често тези функции некоректно биват отнасяни към базовите функции на (непрекъснато) преобразуване. Фактически, както при непрекъснатото Фурие преобразуване, тук няма базис на непрекъснатото уейвлет преобразуване. Време-честотната интерпретация използва малко по-различна формулировка (по Delprat).

Ограничения：

(1) ${\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt$ когато a1 = a и b1 = b,

(2) $\Psi (t)$ има краен времеви интервал.

Сравнение с Фурие преобразуванията (с непрекъснато време)

Уейвлет преобразуванията често се сравняват с преобразувания на Фурие, в което сигналите са представяни като една сума от синусоиди. Основната разлика е в това, че уейвлетите са локализирани едновременно и по честота и по време, докато при стандартното преобразуване на Фурие има само локализация по честота.

Кратковременното Фурие преобразуване КВФП или Short-time Fourier transform, STFT повече прилича на уейвлет преобразуването, като при него има и честотна и времева локализация, но там има проблеми с разделителната способност (резолюцията) по честота/време. Уейвлетите често дават едно по-добро представяне на сигнала, ползвайки Мултирезолюционен анализ, който балансира разделителната способност за произволни време и честота. Дискретното уейвлет преобразуване е по-несложно (или икономично като изчисления), заема като време O(N), сравнено с времето O(N log N), необходимо за Бързо Фурие преобразование.

Това предимство като изчислителна сложност не е присъщо на трансформацията, но отразява избора на логаритмично разделяне по честота, за разлика от равномерно разпределени по честота раздели (прозорци) на БПФ (Бързо Фурие Преобразуване), ползват се същите базисни функции като при ДПФ (Дискретното Фурие Преобразуване).^[2]Тази сложност единствено може да се прилага, когато размера на филтъра не зависи от размера на сигнала.

Определение за уейвлет

Съществуват няколко начина за определяне на уейвлет (или семейство уейвлети).

Мащабиращ филтър (Скейлинг филтър)

Един ортогонален уейвлет е напълно дефиниран чрез мащабиращ филтър – един нискочестотен – крайна импулсна характеристика – КИХ или FIR филтър с дължина 2N плюс 1. При биортогонални уейвлети, са дефинирани отделни филтри за разлагане и филтри за възстановяване.

При анализ с ортогонални уейвлети вискочестотния филтър се построява (пресмята) като квадратурно огледален филтър на нискочестотния филтър, и филтрите за възстановяване са симетрични във времето (обратен ред на време) за фитрите за разлагане.

Уейвлетите на Добеши (Daubechies) и симлетите (symlet) могат да се дефинират чрез мащабиращ филтър.

Мащабираща функция

Уейвлетите се определят чрез уейвлет функцията ψ(t) (т.е. майчиния уейвлет) и мащабиращата (скалиращата) функция φ(t) (наричана също бащин уейвлет) във времевата област.

Тази уейвлет функция по същество е един нискочестотен филтър и мащабирането ѝ за всяко ниво намалява двойно честотна му лента. Това създава проблем в това че, за да се покрие целия спектър, ще са необходими безкрайно количесто нива.

За уейвлети с компактен носител, φ(t) може да се приема за крайна по дължина и е еквивалентна на мащабиращ филтър g.

Уейвлетите на Meyer могат да бъдат определни чрез мащабиращи функции.

Уейвлетна функция

Уейвлетът има представяне във времевата област единствено като уейвлетната функция ψ(t).

Всъщност, Мексиканска шапка уейвлет може да се дефинира чрез уейвлетна функция. Вижте един списък с няколко Непрекъснати уейвлети.

Приложения на дискретото уейвлетно преобразуване

Най-общо, една апроксимация на DWT се ползва за компресиране на данни ако сигнала е вече дискретизиран, и непрекъснато уейвлет преобразуване – CWT за анализ на сигнали. Така, апросимацията с DWT най-често се ползва в техническите науки и компютръните науки, и непрекъснатото или CWT в научните изследвания.

В последно време уейвлет преобразуване е адаптирано за огромен брой приложения, като често замества традиционното Преобразуване на Фурие, или Fourier Transform. В множество области от физиката може да се види това изместване на парадигмата, в това число като молекулярна динамика, ab initio пресмятания или пресмятания от основните принципи, астрофизика, локализация на Плътност на матрици, сеизмология, оптика, турболентност и квантова механика.

Тази промяна също се наблюдава и при обработката на изображения, кръвно налягане, анализи на сърдечен пулс и ЕКГ, мозъчни ритми, ДНК анализ, анализ на протеини, климатология, обща обработка на сигнали, разпознаване на глас, компютърна графика и мултифрактален анализ.

В областта на компютърно зрение и обработка на изображения, идеята за представяне на мащаб-пространство и Гаусови диференциращи оператори се разглежда като едно канонично многомащабно представяне.

Едно възможно приложение на уейвлет апроксимацията е компресирането на данни. Както и при други преобразувания, уейвлет преобразуванията може да се ползват за трансформации на данни, после кодиране на трансформираните данни, и в резултат имаме ефективно компресиране. Например, един известен стандарт за компресиране на изображения, ползващ биортогонални уейвлети е JPEG 2000. Това означава, че макар фрейма да е препълнен, той е един стегнат фрейм, (гл. напр. Фреймове или Векторно пространство), и същите функции на фрейма се използват, както за анализ и така и за синтез, т.е. и в правото и в обратното преобразуване (като се изключи спрегнатостта в комплексните уейвлети). За по-подробна информация в компресиране с уейвлети. В тази връзка се ползва и за изглаждане/обезшумяване на данни на базата на подбиране на праговите стойности на уейвлетните коефициенти, нарича се още свиване (shrinkage). Това може да бъде извършено чрез адаптивно ограничаване на праговете на уейвлетните коефициенти, което съответства на изглаждане и/или обезшумяване на нежелателните честотни компоненти.

Уейвлетните преобразувания започнаха също да се ползват и като комуникационни приложения.

Източници

↑ Ricker, Norman. WAVELET CONTRACTION, WAVELET EXPANSION, AND THE CONTROL OF SEISMIC RESOLUTION // Geophysics 18 (4). 1953. DOI:10.1190/1.1437927.
↑ The Scientist and Engineer's Guide to Digital Signal Processing By Steven W. Smith, Ph.D. Chapter 8. equation 8 – 1.

Paul S. Addison, The Illustrated Wavelet Transform Handbook, Institute of Physics, 2002, ISBN 0-7503-0692-0
Ali Akansu and Richard Haddad, Multiresolution Signal Decomposition: Transforms, Subbands, Wavelets, Academic Press, 1992, ISBN 0-12-047140-X
B. Boashash, editor, „Time-Frequency Signal Analysis and Processing – A Comprehensive Reference“, Elsevier Science, Oxford, 2003, ISBN 0-08-044335-4.
Tony F. Chan and Jackie (Jianhong) Shen, Image Processing and Analysis – Variational, PDE, Wavelet, and Stochastic Methods, Society of Applied Mathematics, ISBN 0-89871-589-X (2005)
Ingrid Daubechies, Ten Lectures on Wavelets, Society for Industrial and Applied Mathematics, 1992, ISBN 0-89871-274-2
Ramazan Gencay, Faruk Selcuk and Brandon Whitcher, An Introduction to Wavelets and Other Filtering Methods in Finance and Economics, Academic Press, 2001, ISBN 0-12-279670-5
Haar A., Zur Theorie der orthogonalen Funktionensysteme, Mathematische Annalen, 69, pp. 331 – 371, 1910.
Barbara Burke Hubbard, „The World According to Wavelets: The Story of a Mathematical Technique in the Making“, AK Peters Ltd, 1998, ISBN 1-56881-072-5, ISBN 978-1-56881-072-0

[1] Ricker, Norman. WAVELET CONTRACTION, WAVELET EXPANSION, AND THE CONTROL OF SEISMIC RESOLUTION // Geophysics 18 (4). 1953. DOI:10.1190/1.1437927.

[2] The Scientist and Engineer's Guide to Digital Signal Processing By Steven W. Smith, Ph.D. Chapter 8. equation 8 – 1.

[1]

[2]