Машинно самообучение
Тази статия вероятно е резултат от машинен превод, има неверен синтаксис и/или неуточнени специални термини и трудно разбираем текст. Ако желаете да помогнете на Уикипедия, използвайте опцията редактиране в горното меню над статията, за да нанесете нужните корекции. |
Тази статия се нуждае от вниманието на редактор с по-задълбочени познания. Ако смятате, че имате необходимите знания, подобрете тази страница. |
Машинното самообучение (МС) е общ термин за „изкуствено“ генериране на знания от опит: изкуствената система се учи от примери и може да ги обобщи след завършване на етапа на обучение. За тази цел алгоритмите в машинното обучение изграждат статистически модел, базиран на данни за обучение. Това означава, че не само се запомнят примери, но се разпознават модели и модели в данните за обучението. По този начин системата може да оцени неизвестни данни (предаване на обучение). Възможни са приложения като: автоматизирани диагностични процедури, откриване на измами с кредитни карти, анализ на фондовия пазар, класификация на нуклеотидни последователности, разпознаване на глас и текст, както и самостоятелна система.
Темата е тясно свързана с „откриване на знания в бази данни“ и „извличане на данни“, но основно става въпрос за намиране на нови модели. Много алгоритми могат да се използват и за двете цели. На свой ред алгоритмите за машинно обучение намират приложение в интелигентния анализ на данните.
Като дисциплина
[редактиране | редактиране на кода]Машинно самообучение е дисциплина, която изучава алгоритмите и математическите модели, използвани от компютърни системи за постепенно подобряване на тяхната ефективност за решаване на множество сходни задачи. Алгоритмите за машинно самообучение изграждат математически модел по примерни данни, наречени „обучаващи данни“, за да прогнозират или да вземат решения, без да са изрично програмирани за това. Тези алгоритми се прилагат в области като филтриране на електронна поща, откриване на неправомерен достъп в компютърни мрежи и компютърно зрение, където съставянето на алгоритми с конкретни инструкции за решаване на задачата е неприложимо. МС е тясно свързано с изчислителната статистика, чийто предмет е прогнозирането с помощта на компютри. То също така черпи методи, теория и сфери на приложение от математическата оптимизация. Извличането на знания от данни е поддисциплина на машинното самообучение, фокусирана върху изследователския анализ на данни чрез обучение без учител. [2][3] Когато се прилага за икономически задачи, машинното самообучение се нарича и прогнозен анализ, който представлява изследване на текущите и предстоящите бизнес показатели с цел изясняване перспективите на неговото развитие.
Терминология
[редактиране | редактиране на кода]Артър Самюел, американски пионер в областта на компютърните игри и изкуствения интелект, въвежда термина „машинно самообучение“ през 1959 г., докато работи за Ай Би Ем.[4][5][6][1]:с. 2 Том М. Мичъл предлага едно често цитирано, по-формализирано определение на алгоритмите, изучавани в областта на МС: „Казваме, че една компютърна програма се учи от опита E по отношение на някакъв клас задачи T и мярка за производителност P, ако производителността ѝ при изпълнение на задачите от T, измерена с P, се подобрява с опита E.“ [7] Това определение на задачите, с които се занимава МС, е по същество операционна дефиниция вместо дефиниция в когнитивни термини. То е в духа на предложението на Алън Тюринг от статията му „Изчислителни машини и разум“, в която въпросът „Могат ли машините да мислят?“ е заменен с „Могат ли машините да правят нещата, които можем да правим ние (в качеството ни на мислещи)?“. [8] В предложението на Тюринг се излагат характеристиките, които биха могли да са присъщи на една мислеща машина и възможните последствия от построяването на такава.
Видове проблеми и задачи
[редактиране | редактиране на кода]
Задачите в областта на МС се класифицират в няколко широки категории. При самообучението с учител (надзиравано МС) алгоритъмът изгражда математически модел на съвкупност от данни, която съдържа и входящите данни, и желаните изходящи резултати. Например, ако задачата е да се определи дали изображение съдържа даден предмет, обучаващите данни за самообучение с учител биха включвали изображения със и без съответния предмет (входящи данни), като всяко изображение има етикет (желан резултат), определящ дали съдържа предмета. В специални случаи входящите данни може да са налице само частично или да са ограничени до специфичен вид обратна връзка.[поясни] Алгоритмите за смесено (отчасти надзиравано) индуктивно самообучение построяват математически модели от непълни обучаващи данни, в които за част от обучаващите примери не е зададен желаният резултат.
Алгоритмите за класификация и регресия спадат към самообучението с учител. Първите се използват, когато желаните резултати се свеждат до ограничен набор от стойности. За класифициращ алгоритъм, който филтрира електронна поща, входът би представлявал получено електронно писмо, а резултатът – името на папката, в която да бъде поставено. За алгоритъм, който разпознава спам, резултатът би бил прогноза от вида „спам“ или „не спам“, представена с булевите стойности единица и нула. Резултатите на алгоритмите за регресионен анализ са непрекъснати величини, което означава, че могат да приемат произволна стойност в даден диапазон. Примери за непрекъснати величини са температурата, дължината или цената на даден предмет.
При самообучението без учител (ненадзиравано МС) алгоритъмът построява математически модел на съвкупност от входящи данни, които не съдържат указания за желаните резултати. Алгоритмите за ненадзиравано самообучение служат за откриване на структура в данните, например групиране или клъстерен анализ. Самообучението без учител може да открива закономерности в данните и да групира входовете в категории, например при извеждане на признаци. Намаляването на размерността представлява процес на редуциране на броя „признаци“, или входове, в съвкупност от данни.
Алгоритмите за активно самообучение получават достъп до желаните резултати (обучаващите етикети) за ограничен набор входящи данни на базата на бюджет и оптимизират избора на входове, за които да поискат обучаващи етикети. При интерактивно използване тези заявки могат да се предоставят на потребител човек за приписване на етикетите. Алгоритмите за обучение с утвърждение получават обратна връзка във вид на положително или отрицателно утвърждение в динамична среда и се използват в автономните автомобили или при самообучение за игра срещу противник човек.[1]:с. 3 Сред специализираните алгоритми в МС е например моделирането на теми, в което на компютърната програма се подава съвкупност от документи на естествен език и тя намира други документи на подобни теми. Алгоритмите за МС могат да се използват за откриване на невъзможна за наблюдение плътност на разпределение в задачи за оценка на плътността. Алгоритмите за метаобучение натрупват индуктивно отместване на базата на опита. В еволюционната роботика алгоритмите за обучение на роботи генерират свои собствени последователности от обучаващи експерименти с цел кумулативно усвояване на нови умения чрез самостоятелно насочвано изследване и социално взаимодействие с хора.
История и връзки с други области
[редактиране | редактиране на кода]Като научна област МС възниква във връзка с усилията за постигане на изкуствен интелект. Още в зората на ИИ като академична дисциплина някои изследователи се интересуват от възможността машините да се самообучават от данни. Те подхождат към задачата с различни символни методи, както и с техники, наречени тогава „невронни мрежи“ – главно перцептрони и други модели, които по-късно се оказват преоткрития на обобщените линейни модели от статистиката.[9] Използват се и разсъждения, базирани на теорията на вероятностите, особено в автоматизираните медицински диагнози.[10]:с. 488
Впоследствие обаче повишаващият се акцент върху логическия, базиран на знания подход предизвиква разрив между ИИ и МС. Вероятностните системи страдат от теоретичните и практическите проблеми на събирането и представянето на данни.[10]:с. 488 До 1980 г. експертните системи вече доминират над ИИ и статистиката е в немилост.[11] Работата по символното/базирано на знания самообучение продължава в рамките на ИИ, водейки до индуктивното логическо програмиране, но изследванията, клонящи повече към статистиката, вече излизат от основния предмет на ИИ и се обособяват в области като разпознаване по шаблони и извличане на информация.[10]:с. 708 – 710; 755 Проучванията в сферата на невронните мрежи са изоставени от ИИ и компютърните науки приблизително по едно и също време. Те продължават извън полето на ИИ/КН под името „конекционизъм“ благодарение на изследователи в други области, включително Джон Хопфилд, Дейвид Румелхарт и Джеф Хинтън. Техният основен успех идва в средата на 80-те години с повторното изобретяване на обратното разпространение на грешката.[10]:с. 25
МС, реорганизирано като отделна дисциплина, започва да процъфтява през 90-те години. Целта му се променя от постигане на изкуствен интелект към справяне с решими задачи от практическо естество. Фокусът му се измества от символните подходи, наследени от ИИ, към методи и модели, заети от статистиката и теорията на вероятностите.[11] От полза му е и повишаващата се достъпност на информация в цифров вид, както и възможността за разпространяването ѝ чрез Интернет.
Връзка с извличането на знания от данни
[редактиране | редактиране на кода]Машинното самообучение и извличането на знания от данни (ИЗД) често използват едни и същи методи и значително се застъпват, но докато МС се фокусира върху прогнозирането, базирано на известни свойства, научени от обучаващите данни, извличането на знания от данни се съсредоточава върху откриването на (преди това) неизвестни свойства в данните (това е етапът на анализ при откриването на знания в бази от данни). ИЗД използва много методи от МС, но с различни цели. От друга страна МС също използва методите на ИЗД като „самообучение без учител“ или като стъпка на предварителна обработка за подобряване на точността на ученето. Голяма част от объркването между тези две изследователски общности (които често имат отделни конференции и отделни списания, с важното изключение на ECML PKDD) идва от базовите предположения, с които работят: в МС производителността обикновено се оценява по отношение на способността да се възпроизвежда вече известно знание, докато при откриването на знания и извличането на знания от данни (ОЗИЗД) основната задача е откриването на неизвестно дотогава знание. Оценен по отношение на известното знание, неинформираният (ненадзираван) метод лесно ще бъде надминат от надзираваните методи, докато в типичните задачи в ОЗИЗД не могат да се използват надзиравани методи поради липсата на обучаващи данни.
Връзка с оптимизацията
[редактиране | редактиране на кода]МС има съществени връзки и с оптимизацията: много задачи за самообучение са формулирани посредством минимизиране на целева функция за набор от обучаващи примери. Целевата функция оценява несъответствието между прогнозираната от обучавания модел стойност и истинската стойност (например при класифициране искаме да приписваме етикети на обекти и моделите се обучават да предсказват правилно предварително зададените етикети за набор от примери; пример за целева функция е „броят на погрешно класифицираните обекти“). Разликата между двете области произлиза от целта на обобщаването: алгоритмите за оптимизация са в състояние да минимизират целевата функция за обучаващите примери, но целта на МС е тя да бъде минимизирана за все още неизвестни примери.[12]
Връзка със статистиката
[редактиране | редактиране на кода]Машинното самообучение е тясно свързано със статистиката. Според Майкъл И. Джордан идеите на МС, от методологичните принципи до теоретичните инструменти, имат дълга предистория в статистиката.[13] Той също така предлага термина data science (наука за данните) като временно име за обединената дисциплина.[13]
Лео Брейман разграничава два модела статистически парадигми: модел на данните и алгоритмичен модел,[14] където „алгоритмичен модел“ означава повече или по-малко алгоритми на машинното самообучение.
Някои статистици са възприели методи от машинното самообучение, давайки начало на комбинирана дисциплина, която те наричат статистическо самообучение.[15]
Теория
[редактиране | редактиране на кода]Основната цел на учещия се е да обобщава от своя опит.[1] В разглеждания контекст обобщаването е способността на обучаваната машина да се справя с висока точност с нови, неизвестни примери/задачи, след като ѝ е била предоставена съвкупност от обучаващи данни. Обучаващите примери се подчиняват на някакво – обикновено неизвестно – вероятностно разпределение, считано за представително за пространството от разглежданите случаи, и обучаваната машина трябва да изгради общ модел за това пространство, който да ѝ позволява извеждането на достатъчно точни прогнози за нови случаи.
Изчислителният анализ на алгоритмите за машинно самообучение и тяхната производителност е дял от теоретичната информатика, познат като теория на изчислителното обучение. Тъй като обучаващите данни са ограничени и бъдещето е неизвестно, теорията на обучението обикновено не дава гаранции за производителността на алгоритмите. Вместо това, производителността често бива оценявана чрез вероятностните си граници. Разлагането изместване/дисперсия е един от начините за количествено оценяване на грешката при обобщаване.
За постигане на най-добра точност на обобщението сложността на хипотезата трябва да съответства на сложността на функцията, описваща данните. Ако хипотезата е има по-ниска сложност от функцията, моделът не осигурява достатъчна апроксимация на данните. Ако реагираме с усложняване на модела, грешката при обучение намалява. Но ако хипотезата е твърде сложна, се получава прекалено близка апроксимация (моделът е преобучен) и по-лошо обобщение.[16]
Освен границите на производителността теоретиците в областта на изчислителното обучение изучават времевата сложност и приложимостта на обучението. В теорията на изчислителното обучение едно изчисление се счита за приложимо, ако може да бъде извършено за полиномиално време. Има два вида резултати по отношение на времевата сложност. Положителните резултати показват, че функциите от определен клас могат да бъдат научени за полиномиално време, а отрицателните – че определени класове не могат да бъдат научени за полиномиално време.
Подходи
[редактиране | редактиране на кода]Видове алгоритми за самообучение
[редактиране | редактиране на кода]Видовете алгоритми за машинно самообучение се различават по възприетия подход, по типа на входящите и изходящите данни и по вида на задачата или проблема, който са предназначени да решават.
Самообучение с учител и смесено самообучение
[редактиране | редактиране на кода]Алгоритмите за надзиравано самообучение построяват математически модел на съвкупност от данни, която съдържа входа и желания изход.[17] Тази съвкупност се нарича обучаващи данни и представлява набор от обучаващи примери. Всеки обучаващ пример съдържа една или повече входни стойности и желана изходяща стойност, наричана още контролен сигнал. При смесените алгоритми в някои от обучаващите примери липсва желаната изходяща стойност. В математическия модел всеки обучаващ пример е представен като масив или вектор, а обучаващите данни като цяло – с матрица. Чрез итеративен процес алгоритъмът за надзиравано самообучение изгражда и оптимизира функция, която може да се използва за прогнозиране на изходящата стойност, свързана с нов набор от входящи стойности.[18] Оптималната функция би позволявала на алгоритъма да определя правилния резултат за входни стойности, които не са част от обучаващите данни. За алгоритъм, който с времето подобрява точността на резултатите или прогнозите си, се казва, че се е обучил да решава дадената задача.[7]
Сред алгоритмите за самообучение с учител се нареждат класификацията и регресионният анализ. [19] Алгоритмите за класификация се използват, когато на изхода се очакват стойности от ограничен набор, а регресионните алгоритми – когато резултатът може да приема произволна числова стойност в рамките на даден интервал. Самообучението по подобие е област от надзираваното МС, тясно свързана с регресията и класификацията, но при него целта е от примерите да се изведе функция на подобие, която измерва колко сходни или свързани са два обекта. То се прилага в задачи, свързани с ранжиране, генериране на препоръки, визуално проследяване на самоличност и разпознаване на лица и гласове.
Самообучение без учител
[редактиране | редактиране на кода]Алгоритмите за ненадзиравано самообучение приемат съвкупност от данни, съдържаща само входящи стойности, и намират структура в данните, например групи или клъстери. Тези алгоритми се обучават от тестови данни, които не са надписани, класифицирани или категоризирани. Вместо да реагират на обратна връзка, те разпознават общи характеристики в данните и реагират според присъствието или отсъствието на тези характеристики във всяка нова порция данни. Основното приложение на ненадзираваното самообучение е при оценка на плътността в статистиката,[20] макар че то обхваща и други области, свързани с обобщаване и обясняване на признаци в данни.
Клъстерният анализ представлява разпределяне на съвкупност от наблюдения в подмножества (наречени клъстери, на английски: clusters), така че наблюденията в един и същ клъстер да са сходни според един или няколко предварително зададени критерии, а наблюденията от различни клъстери да са несходни. Различните техники за клъстериране работят с различни предположения за структурата на данните, които често се дефинират чрез някаква метрика за сходство и се оценяват, например, по вътрешна компактност, или сходство между членовете на един и същ клъстер, и разделяне, или разлика между клъстерите. Други методи се базират на оценки на плътността и свързаност на графи.
Самообучение с утвърждение
[редактиране | редактиране на кода]Обучението с утвърждение е област от МС, която се занимава с това как даден софтуерен агент да избира действията си в дадена среда, така че да максимизира някаква мярка за кумулативно възнаграждение. Поради общия си характер тази област се изследва в много други дисциплини, например теория на игрите, теория на управлението, операционни изследвания, теория на информацията, оптимизация, базирана на симулации, многоагентни системи, кошерен интелект, статистика и генетични алгоритми.[21][22] При машинното самообучение средата обикновено се представя като Марковски процес на взимане на решения. Много алгоритми за обучение с утвърждение използват техники от динамичното програмиране.[21][22][23] Алгоритмите за обучение с утвърждение не предполагат познаване на точния математически модел на Марковския процес и се използват тогава, когато точните модели са неприложими.[21][22] Те се употребяват например в автономните автомобили и при обучението за игра срещу противник човек.
Процеси и техники
[редактиране | редактиране на кода]Различни процеси, техники и методи могат да се прилагат към един или повече видове алгоритми за МС, за да се подобри ефективността им.
Учене на признаци
[редактиране | редактиране на кода]Няколко алгоритъма за самообучение са насочени към откриването на по-добри представяния на входните данни по време на обучение.[24] Класическите примери включват анализ на основните компоненти и клъстерен анализ. Алгоритмите за учене на признаци (feature learning), наричани още алгоритми за учене на представяния (presentation learning), често се опитват да запазят информацията от входните данни, но същевременно и да я преобразуват по начин, който я прави полезна, често като предварителна стъпка преди извършването на класификация или прогнозиране. Тази техника позволява реконструиране на входните данни, получени от неизвестно вероятностно разпределение, без непременно да се отразяват добре конфигурациите, които са малко вероятни в това разпределение. Така се замества ръчното задаване на признаците, описващи разглежданите обекти, и се позволява на машината едновременно да научи признаците и да ги използва за решаването на определена задача.
Ученето на признаци може да бъде както надзиравано, така и ненадзиравано. В първия случай признаците се научават с помощта на надписани от учителя входни данни. Примерите включват невронни мрежи и надзиравано обучение с речник. Във втория случай признаците се научават от ненадписани входни данни. Примери за това са учене с речник, анализ на независимите компоненти, автоматични кодери (autoencoders), матрична декомпозиция[25] и различни видове клъстерен анализ.[26][27][28]
Алгоритмите за обучение, базирано на многообразия (manifold learning), се опитват да постигат това при ограничението, че наученото представяне е с малка размерност. При алгоритмите с разредено кодиране (sparse coding) ограничението е, че наученото представяне трябва да е разредено, т.е. в математическия модел има голям брой нули. При ученето с мултилинейни подпространства (multilinear subspace learning) представянията с малка размерност се учат директно от тензорни представяния за многоразмерни данни, без те да се преобразуват във вектори с по-висока размерност.[29] Алгоритмите за дълбоко обучение (deep learning) откриват много нива на представяне или йерархия от признаци, като по-абстрактните (от по-високо ниво) признаци се дефинират на базата на тези от по-ниско ниво (или ги генерират). Според някои, за да се смята една машина за интелигентна, научаваните от нея представяния трябва да отделят скритите фактори на вариация, обясняващи данните от наблюденията.[30]
Ученето на признаци е мотивирано от факта, че някои задачи в областта на МС, например класифицирането, често изискват входящите данни да са удобни за обработка от математическа и изчислителна гледна точка. Данните от реалния свят обаче, като изображения, видео и данни от сензори, не се поддават на опитите за алгоритмично дефиниране на характерни признаци. Алтернативата е такива признаци да се откриват чрез преглеждане на конкретните данни, без да се разчита на изрични алгоритми.
Обучение с разреден речник
[редактиране | редактиране на кода]Обучението с разреден речник е метод за учене на признаци, при който обучаващите примери са представени като линейни комбинации на базисни функции и се приема, че представляват разредени матрици. Методът е силно NP-сложен и трудно се решава приблизително.[31] Разпространен евристичен метод за учене с разреден речник е алгоритъмът K-SVD. Обучението с разреден речник се прилага в няколко контекста. При класифициране задачата е да се определи към кои класове принадлежи неизвестен обучаващ пример. За речник, в който вече са изградени всички класове, новият обучаващ пример се свързва с класа с най-добро разредено представяне от съответния речник. Обучението с разреден речник се прилага и при премахването на шум от изображения. Основната идея е, че фрагмент от чисто изображение може да се представи в разреден речник от изображения, а шумът – не.[32]
Дървета на решенията
[редактиране | редактиране на кода]При обучението с дървета на решенията се използва дърво на решенията като прогнозен модел, на базата на който да се преминава от наблюдения относно обект (представени в клоните) към изводи за целевата стойност на обекта (представени в листата). То е един от подходите за прогнозиране, използвани в статистиката, извличането на знания от данни и машинното самообучение. Дървовидните модели, при които целевата променлива може да приема дискретно множество от стойности, се наричат класифициращи дървета. В тези дървовидни структури листата представят етикетите на класове, а клоните – логически конюнкции, които водят до тези етикети. Дърветата на решенията, при които целевата променлива може да заема непрекъснати стойности (обикновено реални числа), се наричат регресионни дървета. Дърветата на решенията могат да се използват в областта на анализа на решения като средство за явно, визуално представяне на решенията и вземането на решения. При ИЗД данните се описват с дърво на решенията и полученото като резултат класифициращо дърво може да се използва като входящи данни за вземане на решения.
Асоциативни правила
[редактиране | редактиране на кода]Обучението с асоциативни правила представлява метод за машинно самообучение, базирано на правила и служи за откриване на връзки между променливи в големи бази от данни. То е предназначено да открива строги закономерности в бази от данни с помощта на някаква мярка за „интересност“.[33] При този подход анализирането на допълнителни данни води до генериране на нови правила. Крайната цел, при достатъчно голяма съвкупност от данни, е да се помогне на машината да наподоби способностите на човешкия мозък за извличане на признаци и абстрактни асоциации по отношение на данни, които още не са били категоризирани.[34]
„Машинно самообучение, базирано на правила“ (МСБП), е общ термин за всички методи за МС, които откриват, научават или модифицират „правила“ с цел съхраняване, манипулиране или прилагане на знания. Ключовата характеристика на алгоритмите за МСБП е идентифицирането и използването на съвкупност от релационни правила, които, взети заедно, представят натрупаните в системата знания. Това е в противоположност на други алгоритми за МС, които обикновено откриват един-единствен модел, който може да се приложи върху произволен обект, за да се получи прогноза.[35] Подходите за МСБП включват самообучаващи се класификатори, обучение с асоциативни правила и изкуствени имунни системи.
На базата на понятието „строги правила“ (strong rules) Ракеш Агравал, Томаш Имелински и Арун Свами предлагат асоциативни правила за откриване на закономерности между продуктите в голям обем данни, записани на касите на супермаркети.[36] Например правилото , открито в данните за продажби в супермаркет, би показало, че ако клиент си купи лук и картофи, е много вероятно да купи също така кайма за хамбургер. Подобна информация може да се използва при вземане на решения за маркетингови дейности от рода на промоции или продуктово позициониране. Освен в анализа на пазарни кошници, днес асоциативните правила се използват в области като анализ на употреба на уебсайтове, разпознаване на неправомерен достъп, непрекъснато производство и биоинформатика. За разлика от анализа на последователности (sequence mining), обучението с асоциативни правила обикновено не взема предвид поредността на обектите нито в отделна трансакция, нито между няколко трансакции.
Самообучаващите се класификатори са семейство от алгоритми за МСБП, в които се съчетават откриващ компонент, обикновено генетичен алгоритъм, и обучаващ компонент, който извършва обучение със или без учител или с утвърждение. Те са предназначени да идентифицират съвкупности от контекстно зависими правила, които колективно съхраняват и прилагат знания „на части“ за изготвяне на прогнози.[37]
Индуктивното логическо програмиране (ИЛП) е подход към ученето на правила, в който се използва логическо програмиране за единно описание за входящите примери, знанията от предметната област и хипотезите. Ако е дадено кодиране на известното знание от предметната област и съвкупност от примери, представени като логическа база от факти, системата за ИЛП ще изведе хипотетична логическа програма, от която следват всички положителни и нито един от отрицателните примери. ИЛП е свързано с областта на индуктивното програмиране, която разглежда всякакви програмни езици (не само логически) като възможност за представяне на хипотези, например функционални програми.
Индуктивното логическо програмиране е особено полезно в биоинформатиката и обработката на естествени езици. Гордън Плоткин и Ехуд Шапиро полагат теоретичните основи за индуктивно машинно самообучение в логическа среда.[38][39][40] Шапиро построява първата му реализация (Model Inference System) през 1981 г.: програма на Prolog, която индуктивно извежда логически програми от положителни и отрицателни примери.[41] Терминът индуктивно тук се отнася до логическа индукция, т.е. предлагане на теория, обясняваща наблюдаваните факти, а не до математическа индукция, която служи за доказване на свойство за всички елементи на строго наредено множество.
Модели
[редактиране | редактиране на кода]Изкуствени невронни мрежи
[редактиране | редактиране на кода]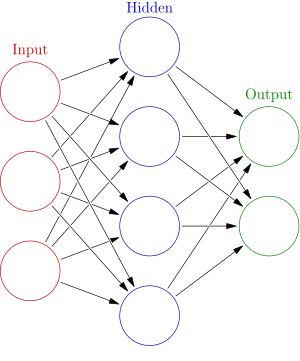
Изкуствените невронни мрежи (ИНМ) (artificial neuron networks, ANN), известни още като конекционистки системи, представляват изчислителни системи, наподобяващи най-общо биологичните невронни мрежи на животинските мозъци.[42] Сама по себе си невронната мрежа не е алгоритъм, а по-скоро рамка, в която могат да работят съвместно много различни алгоритми за МС и да обработват сложни набори от входящи данни.[43] Системите от този тип се „научават“ да решават задачи, като разглеждат примери, обикновено без да са програмирани с правила, специфични за конкретната задача.
ИНМ е модел, базиран на съвкупност от свързани единици или възли, наречени „изкуствени неврони“, които най-общо моделират невроните в биологичен мозък. Всяка връзка, подобно на синапсите в биологичния мозък, може да предава информация, или „сигнал“, от един изкуствен неврон към друг. Изкуственият неврон, получил сигнала, може да го обработи и да сигнализира на други неврони, свързани с него. В разпространените реализации на ИНМ сигналът по връзката между невроните е реално число, а изходът на всеки неврон се изчислява като нелинейна функция на сумата от входовете му. Връзките между изкуствените неврони се наричат „ребра“. Невроните и ребрата обикновено имат тегла, които се настройват при процеса на обучение. Теглото увеличава или намалява силата на сигнала по дадена връзка. Изкуствените неврони могат да имат праг, така че да изпращат сигнал само ако сумираните сигнали надхвърлят този праг. Обикновено изкуствените неврони са организирани в слоеве, които могат да извършват различни видове преобразувания върху входовете си. Сигналите се движат от първия (входния) слой към последния (изходния), евентуално след неколкократно преминаване през слоевете.
Първоначалната цел на подхода с ИНМ е те да решават задачи по същия начин, по който би го правил човешки мозък. С времето обаче фокусът се измества към изпълняване на по-тесни задачи, водейки до отдалечаване от биологията. Изкуствените невронни мрежи се използват в разнообразни области, включително компютърно зрение, разпознаване на реч, машинен превод, филтриране на социални мрежи, игране на настолни и компютърни игри и медицински диагнози.
Дълбокото обучение представлява включване на множество скрити слоеве в изкуствена невронна мрежа. Този подход цели да моделира начина, по който човешкият мозък преработва светлинни и звукови сигнали в зрение и слух. Дълбокото обучение се прилага успешно например в компютърното зрение и разпознаването на реч.[44]
Метод на опорните вектори
[редактиране | редактиране на кода]Методите на опорните вектори (МОВ) [45] (на английски: support vector machines, SVM) са съвкупност от сродни методи за надзиравано самообучение, използвани за класификация и регресия. При даден набор от обучаващи примери, всеки от които е отбелязан като принадлежащ на една от две категории, обучаващият алгоритъм създава модел, който предвижда дали даден нов пример попада в едната или другата категория.[46] Алгоритмите за обучение по МОВ са непробабилистични двоични линейни класификатори, макар че съществуват и методи като калибрацията на Плат, които позволяват използването на МОВ за вероятностна класификация. Освен линейна класификация, моделите с опорни вектори могат да извършват ефикасно и нелинейна класификация чрез трик, наречен метод на ядрото, който установява неявно съответствие между входовете им и пространства от признаци с по-висока размерност.
Мрежи на Бейс
[редактиране | редактиране на кода]
Мрежа на Бейс или насочен ацикличен графов модел е вероятностен графов модел, който представя множество от случайни величини и техните условни зависимости чрез насочен ацикличен граф. Например, с Бейсова мрежа може да се представят вероятностните връзки между болести и симптоми. По дадени симптоми мрежата може да се използва, за да се изчислят вероятностите за наличието на различни болести. Съществуват ефикасни алгоритми за логически извод и обучение. Мрежите на Бейс, моделиращи поредици от величини, например речеви сигнали или белтъчни последователности, се наричат динамични мрежи на Бейс. Едно обобщение на Бейсовите мрежи, което позволява да се представят и решават задачи за вземане на решения в условия на неопределеност, са така наречените диаграми на влиянието (influence diagrams).
Еволюционни алгоритми. Генетични алгоритми
[редактиране | редактиране на кода]Генетичният алгоритъм е евристичен алгоритъм за търсене, който копира процеса на естествен подбор и използва методи като мутация и кръстосване, за да генерира нови генотипи, надявайки се да намери добро решение на даден проблем. Генетичните алгоритми намират приложение в машинното самообучение през 80-те и 90-те години на 20 век.[47][48] Връзката е и в обратна посока: техники от МС се използват за подобряване ефективността на генетичните и еволюционните алгоритми [49].
Класически задачи, решаеми с помощта на машинното обучение
[редактиране | редактиране на кода]- Класификация, изпълнява се с помощта на Обучение с учител на етап на собственното обучение.
- Клъстеризация, също се изпълняна с помощта на Обучение без учител
- Регресия, изпълнява се с помощта на Обучение с учител на етапа на тестването, като частен случай на Задачи по прогнозиране.
- Построение на рангова зависимост
Източници
[редактиране | редактиране на кода]- ↑ а б в г Bishop, C. M. Pattern Recognition and Machine Learning. Springer, 2006. ISBN 0-387-31073-8.
- ↑ Машинното самообучение и разпознаването на шаблони „могат да се считат за две лица на една и съща дисциплина“.[1]:vii
- ↑ Friedman, Jerome H. title=Data Mining and Statistics: What's the connection?. {{{title}}} // Computing Science and Statistics 29 (1). 1998. с. 3 – 9.
- ↑ R. Kohavi and F. Provost, „Glossary of terms“, Machine Learning, vol. 30, no. 2 – 3, pp. 271 – 274, 1998.
- ↑ Samuel, Arthur. Some Studies in Machine Learning Using the Game of Checkers // IBM Journal of Research and Development 3 (3). 1959. DOI:10.1147/rd.33.0210. с. 210 – 229.
- ↑ Определението „без да са изрично програмирани“ често се приписва на Артър Самюел, който въвежда термина machine learning през 1959 г., но фразата не се среща в този вид в споменатото издание и може би е парафраза, появила се по-късно. Вижте „Paraphrasing Arthur Samuel (1959), the question is: How can computers learn to solve problems without being explicitly programmed?“ в Koza, John R. Automated Design of Both the Topology and Sizing of Analog Electrical Circuits Using Genetic Programming // Artificial Intelligence in Design '96. Springer, Dordrecht, 1996, 151 – 170 pp. DOI:10.1007/978-94-009-0279-4_9. (на английски)
- ↑ а б Mitchell, T. Machine Learning. McGraw Hill, 1997. ISBN 978-0-07-042807-2. с. 2.
- ↑ Harnad, Stevan. The Annotation Game: On Turing (1950) on Computing, Machinery, and Intelligence // The Turing Test Sourcebook: Philosophical and Methodological Issues in the Quest for the Thinking Computer. Kluwer, 2008.
- ↑ ."Neural Networks and statistical models".
- ↑ а б в г Russell, Stuart; Norvig, Peter. Artificial Intelligence: A Modern Approach. Prentice Hall. Edition 2}}
- ↑ а б Langley, Pat. The changing science of machine learning // Machine Learning 82 (3). 2011. DOI:10.1007/s10994-011-5242-y. с. 275 – 279.
- ↑ Improving First and Second-Order Methods by Modeling Uncertainty // Optimization for Machine Learning. MIT Press, 2012. с. 404.
- ↑ а б Michael I. Jordan. statistics and machine learning // reddit, 10 септември 2014. Посетен на 1 октомври 2014.
- ↑ Cornell University Library. Breiman: Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author) // Посетен на 8 август 2015.
- ↑ An Introduction to Statistical Learning. Springer, 2013. с. vii. Архив на оригинала от 2019-06-23 в Wayback Machine.
- ↑ Alpaydin, Ethem. Introduction to Machine Learning. London, The MIT Press, 2010. ISBN 978-0-262-01243-0. Посетен на 4 февруари 2017.
- ↑ Russell, Stuart J., Norvig, Peter. Artificial Intelligence: A Modern Approach. Third. Prentice Hall, 2010. ISBN 9780136042594.
- ↑ Mohri, Mehryar, Rostamizadeh, Afshin, Talwalkar, Ameet. Foundations of Machine Learning. The MIT Press, 2012. ISBN 9780262018258.
- ↑ Alpaydin, Ethem. Introduction to Machine Learning. MIT Press, 2010. ISBN 978-0-262-01243-0. с. 9.
- ↑ Neural Networks // Computer Science Handbook, Second Edition (Section VII: Intelligent Systems). Boca Raton, Florida, Chapman & Hall/CRC Press LLC, 2004. ISBN 1-58488-360-X.
- ↑ а б в Dimitri P. Bertsekas. „Dynamic Programming and Optimal Control: Approximate Dynamic Programming, Vol.II“, Athena Scientific, 2012,[1]
- ↑ а б в Dimitri P. Bertsekas and John N. Tsitsiklis. „Neuro-Dynamic Programming“, Athena Scientific, 1996,[2]
- ↑ Reinforcement learning and markov decision processes // Reinforcement Learning. Springer Berlin Heidelberg, 2012. с. 3 – 42.
- ↑ Representation Learning: A Review and New Perspectives // IEEE Trans. PAMI, special issue Learning Deep Architectures 35. 2013. DOI:10.1109/tpami.2013.50. с. 1798 – 1828.
- ↑ Maximum-Margin Matrix Factorization // NIPS (Conference on Neural Information Processing Systems). 2004.
- ↑ An analysis of single-layer networks in unsupervised feature learning // Int'l Conf. on AI and Statistics (AISTATS). 2011. Архив на оригинала от 2017-08-13 в Wayback Machine.
- ↑ Visual categorization with bags of keypoints // ECCV Workshop on Statistical Learning in Computer Vision. 2004.
- ↑ Speech and Language Processing. Pearson Education International, 2009. с. 145 – 146.
- ↑ Lu, Haiping и др. A Survey of Multilinear Subspace Learning for Tensor Data // Pattern Recognition 44. 2011. DOI:10.1016/j.patcog.2011.01.004. с. 1540 – 1551. Архивиран от оригинала на 2019-07-10.
- ↑ Yoshua Bengio. Learning Deep Architectures for AI. Now Publishers Inc., 2009. ISBN 978-1-60198-294-0. с. 1 – 3.
- ↑ Tillmann, A. M. On the Computational Intractability of Exact and Approximate Dictionary Learning // IEEE Signal Processing Letters 22 (1). 2015. DOI:10.1109/LSP.2014.2345761. с. 45 – 49.
- ↑ Aharon, M, M Elad, and A Bruckstein. 2006. „K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation.“ Signal Processing, IEEE Transactions on 54 (11): 4311 – 4322
- ↑ Piatetsky-Shapiro, Gregory (1991), Discovery, analysis, and presentation of strong rules, in Piatetsky-Shapiro, Gregory; and Frawley, William J.; eds., Knowledge Discovery in Databases, AAAI/MIT Press, Cambridge, MA.
- ↑ How Does Association Learning Work? // deepai.org.
- ↑ Bassel, George W. et al. Functional Network Construction in Arabidopsis Using Rule-Based Machine Learning on Large-Scale Data Sets // The Plant Cell 23 (9). 1 септември 2011. DOI:10.1105/tpc.111.088153. p. 3101 – 3116. (на английски)
- ↑ Mining association rules between sets of items in large databases // Proceedings of the 1993 ACM SIGMOD international conference on Management of data – SIGMOD '93. 1993. ISBN 0897915925. DOI:10.1145/170035.170072. с. 207.
- ↑ Urbanowicz, Ryan J. et al. Learning Classifier Systems: A Complete Introduction, Review, and Roadmap // Journal of Artificial Evolution and Applications 2009. 22 септември 2009. DOI:10.1155/2009/736398. p. 1 – 25. (на английски)
- ↑ Plotkin G.D. Automatic Methods of Inductive Inference, PhD thesis, University of Edinburgh, 1970.
- ↑ Shapiro, Ehud Y. Inductive inference of theories from facts, Research Report 192, Yale University, Department of Computer Science, 1981. Reprinted in J.-L. Lassez, G. Plotkin (Eds.), Computational Logic, The MIT Press, Cambridge, MA, 1991, pp. 199 – 254.
- ↑ Shapiro, Ehud Y. (1983). Algorithmic program debugging. Cambridge, Mass: MIT Press. ISBN 0-262-19218-7
- ↑ Shapiro, Ehud Y. "The model inference system." Proceedings of the 7th international joint conference on Artificial intelligence-Volume 2. Morgan Kaufmann Publishers Inc., 1981.
- ↑ Artificial Neural Networks as Models of Neural Information Processing | Frontiers Research Topic // Посетен на 20 февруари 2018. (на английски)
- ↑ Build with AI | DeepAI // DeepAI. Посетен на 6 октомври 2018.
- ↑ Honglak Lee, Roger Grosse, Rajesh Ranganath, Andrew Y. Ng. "Convolutional Deep Belief Networks for Scalable Unsupervised Learning of Hierarchical Representations" Proceedings of the 26th Annual International Conference on Machine Learning, 2009.
- ↑ К. В. Воронцов. Лекции по методу опорных векторов
- ↑ Cortes, Corinna и др. Support-vector networks // Machine Learning 20 (3). 1995. DOI:10.1007/BF00994018. с. 273 – 297.
- ↑ Goldberg, David E. и др. Genetic algorithms and machine learning // Machine Learning 3 (2). 1988. DOI:10.1007/bf00113892. с. 95 – 99.
- ↑ Michie, D. и др. Machine Learning, Neural and Statistical Classification // Ellis Horwood Series in Artificial Intelligence. 1994.
- ↑ Zhang, Jun; Zhan, Zhi-hui; Lin, Ying; Chen, Ni; Gong, Yue-jiao; Zhong, Jing-hui; Chung, Henry S.H.; Li, Yun; Shi, Yu-hui (2011). „Evolutionary Computation Meets Machine Learning: A Survey“ (PDF). Computational Intelligence Magazine (IEEE) 6(4): 68 – 75. doi:10.1109/mci.2011.942584.
| Тази страница частично или изцяло представлява превод на страницата „Машинное обучение“ и страницата Machine learning в Уикипедия на руски и английски език. Оригиналните текстове, както и този превод, са защитени от Лиценза „Криейтив Комънс – Признание – Споделяне на споделеното“, а за творби, създадени преди юни 2009 година – от Лиценза за свободна документация на ГНУ. Прегледайте историята на редакциите на оригиналните страници тук и тук, за да видите списъка на техните съавтори.
ВАЖНО: Този шаблон се отнася единствено до авторските права върху съдържанието на статията. Добавянето му не отменя изискването да се посочват конкретни източници на твърденията, които да бъдат благонадеждни. |
Допълнителни източници
[редактиране | редактиране на кода]- Флах П. Машинное обучение ДМК Пресс М. стр. 400 2015. isbn 978-5-97060-273-7.
- Шлезингер М., Главач В. Десять лекций по статистическому и структурному распознаванию. – Киев: Наукова думка, 2004. ISBN 966-00-0341-2.
- Gergana Lazarova, Milen Chechev, Ivan Koychev, A Multi-View Learning Algorithm, 7th National Conference Education studies in the Information Society – Sofia University „Kliment Ohridski“, Bulgaria, 2014
- Ian H. Witten and Eibe Frank (2011). Data Mining: Practical machine learning tools and techniques Morgan Kaufmann, 664pp., ISBN 978-0-12-374856-0.
- Sergios Theodoridis, Konstantinos Koutroumbas (2009) „Pattern Recognition“, 4th Edition, Academic Press, ISBN 978-1-59749-272-0.
- Mierswa, Ingo and Wurst, Michael and Klinkenberg, Ralf and Scholz, Martin and Euler, Timm: YALE: Rapid Prototyping for Complex Data Mining Tasks, in Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD-06), 2006.
- Bing Liu (2007), Web Data Mining: Exploring Hyperlinks, Contents and Usage Data. Springer, ISBN 3-540-37881-2
- Toby Segaran (2007), Programming Collective Intelligence, O'Reilly, ISBN 0-596-52932-5
- Huang T.-M., Kecman V., Kopriva I. (2006), Kernel Based Algorithms for Mining Huge Data Sets, Supervised, Semi-supervised, and Unsupervised Learning, Springer-Verlag, Berlin, Heidelberg, 260 pp. 96 illus., Hardcover, ISBN 3-540-31681-7.
- Ethem Alpaydın (2004) Introduction to Machine Learning (Adaptive Computation and Machine Learning), MIT Press, ISBN 0-262-01211-1
- MacKay, David J. C.. Information Theory, Inference, and Learning Algorithms Cambridge: Cambridge University Press, 2003. ISBN 0-521-64298-1
- Kecman Vojislav (2001), Learning and Soft Computing, Support Vector Machines, Neural Networks and Fuzzy Logic Models, The MIT Press, Cambridge, MA, 608 pp., 268 illus., ISBN 0-262-11255-8.
- Trevor Hastie, Robert Tibshirani and Jerome Friedman (2001). The Elements of Statistical Learning Архив на оригинала от 2009-11-10 в Wayback Machine., Springer. ISBN 0-387-95284-5.
- Richard O. Duda, Peter E. Hart, David G. Stork (2001) Pattern classification (2nd edition), Wiley, New York, ISBN 0-471-05669-3.
- Bishop, C.M. (1995). Neural Networks for Pattern Recognition, Oxford University Press. ISBN 0-19-853864-2.
- Ryszard S. Michalski, George Tecuci (1994), Machine Learning: A Multistrategy Approach, Volume IV, Morgan Kaufmann, ISBN 1-55860-251-8.
- Sholom Weiss and Casimir Kulikowski (1991). Computer Systems That Learn, Morgan Kaufmann. ISBN 1-55860-065-5.
- Yves Kodratoff, Ryszard S. Michalski (1990), Machine Learning: An Artificial Intelligence Approach, Volume III, Morgan Kaufmann, ISBN 1-55860-119-8.
- Ryszard S. Michalski, Jaime G. Carbonell, Tom M. Mitchell (1983), Machine Learning: An Artificial Intelligence Approach, Tioga Publishing Company, ISBN 0-935382-05-4.
- Ryszard S. Michalski, Jaime G. Carbonell, Tom M. Mitchell (1986), Machine Learning: An Artificial Intelligence Approach, Volume II, Morgan Kaufmann, ISBN 0-934613-00-1.
- Vladimir Vapnik (1998). Statistical Learning Theory. Wiley-Interscience, ISBN 0-471-03003-1.
- Ray Solomonoff, An Inductive Inference Machine, IRE Convention Record, Section on Information Theory, Part 2, pp., 56 – 62, 1957.
- Ray Solomonoff, "An Inductive Inference Machine" A report from the 1956 Dartmouth Summer Research Conference on AI.
Software
[редактиране | редактиране на кода]- GNU R e безплатно статистическо программно обезпечение, достъпно на различни платформи, с расширение за машинно обучения и интелектуален анализ на данни
- Matlab e програма с потребителски интерфейс за машинно обучение
Външни препратки
[редактиране | редактиране на кода]- www.MachineLearning.ru – профессионален уики-ресурс, посветен на машинното обучение и интеллектуалния анализ на данни
- Международно общество за Машинно обучение
- Популярен онлайн курс от Андрю Ндж, Coursera. Ползва GNU Octave. Курсът е свободна версия на станфордския курс, преподаван от Ндж, които също са онлайн на сайта на университета for free.
- mloss – академична база данни от open-source machine learning software.

