Пирамида

Вижте пояснителната страница за други значения на Пирамида.

Пирамѝдата (от старогръцки: πυραμίς, род. п. πυραμίδος) е геометрично тяло, многостен, образуван от свързването на всеки от върховете на n-ъгълник (n = 3, 4,...), наречен основа, с точка, нележаща в равнината му, наречена връх на пирамидата. Стените, едната страна на които е и страна на основата, а другите 2 сключват помежду си ъгъл при върха на пирамидата, се наричат околни стени или странични стени. Ръбовете при основата се наричат основни ръбове, а останалите ръбове на пирамидата – околни ръбове или странични ръбове.

Околните стени на пирамидата са триъгълници. Отсечката, спусната от върха към равнината на основата и образуваща прав ъгъл с нея, се нарича височина. Височината на околна стена, спусната от върха на пирамидата към основния ръб, се нарича апотема. Сборът от лицата на околните стени на пирамидата се нарича околна повърхнина (или странична повърхнина), а сборът от околната повърхнина и лицето на основата – пълна повърхнина. ^[1]

Пирамидата е частен случай на конус. ^[2].

Видове пирамиди

Права пирамида – пирамида, пета̀та на височината на която е център на основата, който е център на вписаната в нея окръжност.
Наклонена пирамида – пирамида, петата на височината на която не е център на основата.
Правоъгълна пирамида – наклонена пирамида, на която един от околните ръбове е перпендикулярен на основата. Този ръб е височината на пирамидата.
Правилна пирамида – пирамида с основа правилен многоъгълник и равни околни ръбове.

Наклонена петоъгълна пирамида
Правоъгълна четириъгълна пирамида
Пресечена правилна петоъгълна пирамида
Триъгълна пирамида (тетраедър)

Пресечена пирамида – многостен, заключен между основа на пирамида и нейно успоредно сечение.
Тетраедър – триъгълна пирамида.
Правоъгълен тетраедър – тетраедър, на който трите ъгъла при един връх са равни.
Правилен тетраедър – тетраедър, на който четирите страни са еднакви равностранни триъгълници.

Означения

Означения на пирамиди

Една права пирамида може да бъде означена като ( )∨P, където ( ) е точката на върха, ∨ е оператор за свързване, а P е многоъгълникът на основата.

Равнобедрен триъгълен прав тетраедър може да бъде записан
( )∨[( )∨{ }] като съединение на точка с основата на пирамидата равнобедрен триъгълник,
а също и [( )∨( )]∨{ } или { }∨{ } като съединение (ортогонални отмествания) на два ортогонални сегмента, равностенен тетраедър с 4 стени равнобедрени триъгълници. Той има симетрия C_1v от две различни ориентации основа-връх и пълна симетрия C_2v.

Прави неправилни пирамиди
Правоъгълна пирамида	Ромбична пирамида	Шестоъгълна изпъкнало-вдлъбната пирамида

Права правоъгълна пирамида се записва ( )∨[{ }×{ }],
а ромбична пирамида – ( )∨[{ }+{ }], и двете имат симетрия C_2v.

Означения на елементите

Елементите на пирамидата са означени със следните латински букви:

$b$ – основен ръб (страната на основата на пирамидата)
$l$ – околен ръб
$h$ – височина
$a$ – апотема на пирамидата
$r$ – апотема на основата или радиус на вписаната окръжност (ако основата е правилен многоъгълник)

Повърхнина и обем

Лицето на основната повърхнина на правилна пирамида се намира по формулата:

B={\frac {P.r}{2}}

,

където ${P}$ е периметърът на основата, а ${r}$ е апотемата на основата.

Лицето на околната повърхнина на неправилна пирамида се намира като сума от лицата на околните стени:

S_{b}=\sum _{i}^{n}S_{i}={\frac {1}{2}}\sum _{i}^{n}(b_{i}.a_{i}),

където $a_{i}$ са апотемите на пирамидата за всяка околна стена от върха към основните ръбове $b_{i}$ .

Лицето на околната повърхнина на правилна пирамида се намира по формулата:

S_{ok}={\frac {P.a}{2}}={\frac {n}{2}}l^{2}\sin \alpha

,

където ${a}$ е апотемата на пирамидата, ${l}$ е околният ръб, ${n}$ е броят на страните на основата, $\alpha$ е плоският ъгъл при върха на пирамидата.

Лицето (площта) на пълната повърхнина на произволна пирамида е сума от лицата на основната и околната повърхнини

S=B+S_{ok}

Лицето (площта) на пълната повърхнина на правилна пирамида се пресмята по формулата:

S=B+S_{ok}={\frac {P(a+r)}{2}}.

Лице на основата и височина на пирамиди.

Обемът на произволна пирамида се намира по формулата:

V={\frac {B.h}{3}}

,

където ${B}$ е лицето на основата, а ${h}$ е височината на пирамидата.
Той е ${\frac {1}{6}}$ от обема на паралелепипеда ${\textstyle \ V_{nap}}$ с основа и височина като на пирамидата:

V={\frac {V_{nap}}{6}}

.

Обемът на триъгълна пирамида (тетраедър) също може да бъде изчислен по формулата ^[3]:

V={\frac {1}{6}}b_{i}l_{i+1}d\sin \varphi ,

където $b_{i},l_{i+1}$ са противоположни (непресичащи се) ръбове,
$d$ е разстоянието между тях ( $b_{i}$ ⊥ $d$ ⊥ $l_{i+1}$ ), $\varphi$ е ъгъл между $b_{i}$ и $l_{i+1}$ .

Пресечена пирамида

Основна статия: Пресечена пирамида

Равнина, успоредна на основата на пирамида, отсича от нея пирамида с по-малка височина. Така полученото тяло се нарича пресечена пирамида, а малката отсечена пирамида – допълнителна пирамида. За лицата на двете основи на пресечената пирамида е изпълнено равенството:

$B_{1}:B_{2}={h_{1}}^{2}:{h_{2}}^{2}$ .

Околните стени са трапеци. Пълната повърхнина на пресечена пирамида е сборът от лицата на тези трапеци и лицата на двете основи. Площта на околната повърхност е равна на произведението от половината от сумата на периметрите на нейните основи и апотемата (височината на страничната повърхност):

S_{ok}={\frac {p_{1}+p_{2}}{2}}\cdot a

,

където $p_{1}$ е периметър на първата основа, $p_{2}$ – периметър на втората, $a$ – апотема.

Обемът на пресечена пирамида с лица на основите $B_{1}$ и $B_{2}$ и височина $h$ е

V={\frac {h}{3}}(B_{1}+B_{2}+{\sqrt {B_{1}B_{2}}}).

Разгъната пирамида

Развивката или разгънатото тяло е плоска фигура, получена чрез съвместяване на повърхността на геометрично тяло с една равнина (без налагане на стени или други повърхностни елементи един върху друг). При пирамидата се получава чрез разрязване по околните или основни ръбове. Пристъпвайки към изучаване на развивката на повърхностността, препоръчително е тя да се разглежда като гъвкава, неразтеглива плоскост. Някои от повърхнините, представени по този начин, могат да бъдат съвместени с равнина чрез огъване. Освен това, ако отрязък от повърхността може да се съвмести с равнина без прекъсвания и залепвания, тогава такава повърхност се нарича разгъваща се, а получената плоска фигура се нарича нейна развивка.

Свойства

При равни околни ръбове

Ако всички околни (странични) ръбове са равни, тогава:

пирамидата е права;
обратното също е вярно, т.е. ако пирамидата е права, всички околни (странични) ръбове са равни;
около основата на пирамида може да се опише окръжност, като върхът на пирамидата е в центъра ѝ;
околните ръбове образуват равни ъгли с равнината на основата;
обратното също е вярно, т.е. ако страничните ръбове образуват равни ъгли с равнината на основата или ако около основата на пирамида може да се опише окръжност, като върхът на пирамидата е в центъра ѝ, тогава всички странични ръбове на пирамидата са равни.

При еднакъв наклон на околните стени

Ако околните (страничните) стени са наклонени спрямо равнината на основата под еднакъв ъгъл, тогава:

в основата на пирамидата може да се впише окръжност, като върхът на пирамидата е проектиран в нейния център;
височините на страничните стени са равни;
площта на околната повърхност е равна на половината от произведението на периметъра на основата и височината на страничната стена.

Правилна пирамида

При правилната пирамида:

околните стени са еднакви триъгълници, а ако е пресечена – еднакви трапеци;
двустенните ъгли между околните стени и основата (при пресечена пирамида – основите) са равни;
двустенните ъгли между околните стени са равни;
поради равенството на околните ръбове пирамидата е винаги права.

Права пирамида

Околните стени на правата пирамида сключват равни двустенни ъгли с основата.
Обратното също е вярно, т.е. ако околните стени на пирамида сключват равни двустенни ъгли с основата, пирамидата е права.

Характеристики и параметри

Обща пирамида

Ако основата е многоъгълник с $n$ върха, площ $B$ и височина $h$ , тогава:^[4]

Брой ъгли	$n+1$
Брой ръбове	$2\cdot n$
Брой лица	$n+1$
Обем	$V={\tfrac {1}{3}}\cdot B\cdot h$
Височина на центъра на тежестта	$s={\frac {h}{4}}$
Фигура за $n=5$

Медицентърът $C'$ на пирамидата разделя отсечката между центъра на основата $C$ и върха $S$ в съотношение $1:3$ .

В случай че $n=3$ , пирамидата се нарича тетраедър.

Всяка пирамида е самодуална по отношение на разположението на своите върхове, ръбове и стени.

Права квадратна пирамида

Правата квадратна пирамида е правилна четириъгълна пирамида.

Нека $a$ е дължината на страната на квадратната основа, а $h$ е височината на пирамидата. Тогава правилната квадратна пирамида има следните параметри:

Брой ъгли	5
Брой ръбове	8
Брой лица	5
Дължина на околните ръбове	$l={\sqrt {h^{2}+{\frac {a^{2}}{2}}}}$
Височина на равнобедрените триъгълници	$h'={\sqrt {h^{2}+{\frac {a^{2}}{4}}}}$
Площ на равнобедрения триъгълник	${\frac {a}{2}}\cdot {\sqrt {h^{2}+{\frac {a^{2}}{4}}}}$
Обем	$V={\frac {1}{3}}\cdot a^{2}\cdot h$
Площ	$S=a^{2}+a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}$

Дефиниция като Джонсоново тяло

Квадратна пирамида, чиито четири триъгълни стени са равностранни триъгълници, е най-простото Джонсоново тяло, означено съкратено с $J_{1}$ . В този случай $h={\frac {a}{2}}\cdot {\sqrt {2}}$ и пирамидата е половин правилен октаедър.

Максимален обем

Ако за всички правилни квадратни пирамиди с дадена площ $S$ се търсят тези с най-голям обем $V$ , тогава дължината на страната $a$ и височината $h$ могат да бъдат определени като функция на $S$ .

Едно извеждане за тези величини е следното:

Решава се уравнението
$S=a^{2}+a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}$
за $h^{2}$ , замества се единственото решение за $h^{2}$ в диференцируемата функция
$U(a)=9\cdot V^{2}=a^{4}\cdot h^{2}$
и се определя локалния максимум на $U$ . Тук площта на повърхността $S$ е дадена константа, а дължината на страната $a$ е променливата на функцията $U$ . Параметрите $S,V,a$ и $h$ са положителни реални числа.

Прилагайки верижното правило на диференциалното смятане към функцията $U(a)=9\cdot (V(a))^{2}$ , се получава:

$U'(a)=18\cdot V(a)\cdot V'(a)$

Тъй като $V(a)>0$ , обемната функция $V$ има локален екстремум точно в точките $a$ , където функцията $U$ има локален екстремум. Това води до следното единствено решение:

a={\frac {\sqrt {S}}{2}}

h={\sqrt {\frac {S}{2}}}

Следователно,

h={\sqrt {2}}\cdot a

Като е дадена площта на повърхността, всички размери на квадратната пирамида с максимален обем са еднозначно определени. За този обем важи

V={\frac {1}{3}}\cdot a^{3}\cdot {\sqrt {2}}={\frac {S\cdot {\sqrt {S}}}{12\cdot {\sqrt {2}}}}={\frac {\sqrt {2}}{24}}\cdot S^{\frac {3}{2}}

.

Формули за правилни пирамиди

Таблица

Следващата таблица съдържа формули за геометричните размери на правилни пирамиди: обща, квадратна и триъгълна.

Размери на правилна пирамида (с височина $h$ и основа правилен $n$ -ъгълник с дължина на страната $a$ )
	Общ случай	Квадратна пирамида ( $n=4$ )	Правилна триъгълна пирамида ( $n=3$ )
Обем	$V={\frac {n\cdot a^{2}\cdot h}{12}}\cdot \cot \left({\frac {\pi }{n}}\right)$	$V={\frac {a^{2}\cdot h}{3}}$	$V={\frac {a^{2}\cdot h}{12}}\cdot {\sqrt {3}}$
Площ	$S={\frac {na}{4}}\left(a\cdot \cot \left({\frac {\pi }{n}}\right)+{\sqrt {4h^{2}+a^{2}\cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)$	$S=a^{2}+a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}$	$S={\frac {3a}{4}}\left({\frac {a{\sqrt {3}}}{3}}+{\sqrt {4h^{2}+{\frac {a^{2}}{3}}}}\right)$
Дължина на околния ръб	$l=\left(h^{2}+{\frac {a^{2}}{4\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}$	$l={\sqrt {h^{2}+{\frac {a^{2}}{2}}}}$	$l={\sqrt {h^{2}+{\frac {a^{2}}{3}}}}$
Радиус на описаната сфера	$r_{o}={\frac {h}{2}}+{\frac {a^{2}}{8\cdot h\cdot \sin ^{2}\left({\frac {\pi }{n}}\right)}}$	$r_{o}={\frac {h}{2}}+{\frac {a^{2}}{4\cdot h}}$	$r_{o}={\frac {h}{2}}+{\frac {a^{2}}{6\cdot h}}$
Радиус на вписаната сфера	$r_{b}={\frac {a\cdot h}{a+{\sqrt {4\cdot h^{2}\cdot \tan ^{2}\left({\frac {\pi }{n}}\right)+a^{2}}}}}$	$r_{b}={\frac {a\cdot h}{a+{\sqrt {4\cdot h^{2}+a^{2}}}}}$	$r_{b}={\frac {a\cdot h}{a+{\sqrt {12\cdot h^{2}+a^{2}}}}}$
Вътрешен ъгъл на правилната основа	$\alpha ={\frac {n-2}{n}}\cdot 180^{\circ }$	$\alpha =90^{\circ }$	$\alpha =60^{\circ }$
Ъгли при основата на околните стени	$\alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}{\sqrt {4h^{2}+a^{2}\cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)$	$\alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}{\sqrt {4h^{2}+a^{2}}}\right)$	$\alpha _{1}=\alpha _{2}=\arctan \left({\frac {1}{a}}{\sqrt {4h^{2}+{\frac {a^{2}}{3}}}}\right)$
Ъгъл при върха на околните равнобедрени триъгълници	$\alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+a^{2}\cdot \cot ^{2}\left({\frac {\pi }{n}}\right)}}}\right)$	$\alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+a^{2}}}}\right)$	$\alpha _{3}=2\cdot \arctan \left({\frac {a}{\sqrt {4\cdot h^{2}+{\frac {a^{2}}{3}}}}}\right)$
Двустенен ъгъл между основата и околната стена	$\beta _{1}=\arctan \left({\frac {2\cdot h\cdot \tan \left({\frac {\pi }{n}}\right)}{a}}\right)$	$\beta _{1}=\arctan \left({\frac {2\cdot h}{a}}\right)$	$\beta _{1}=\arctan \left({\frac {2\cdot {\sqrt {3}}\cdot h}{a}}\right)$
Двустенен ъгъл между околните стени	$\beta _{2}=2\arctan \left({\frac {1}{2h}}\left({\frac {4h^{2}\sin ^{2}\left({\frac {\pi }{n}}\right)+a^{2}}{\tan ^{2}\left({\frac {\pi }{n}}\right)-\sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}\right)$	$\beta _{2}=2\arctan \left({\frac {1}{2h}}{\sqrt {4h^{2}+2a^{2}}}\right)$	$\beta _{2}=2\arctan \left({\frac {1}{3h}}\cdot {\sqrt {3h^{2}+a^{2}}}\right)$
Ъгъл между страничния ръб и основата	$\gamma _{1}=\arctan \left({\frac {2\cdot h\cdot \sin \left({\frac {\pi }{n}}\right)}{a}}\right)$	$\gamma _{1}=\arctan \left({\frac {{\sqrt {2}}\cdot h}{a}}\right)$	$\gamma _{1}=\arctan \left({\frac {{\sqrt {3}}\cdot h}{a}}\right)$
Ъгъл между височината и страничния ръб	$\gamma _{2}=\arctan \left({\frac {a}{2\cdot h\cdot \sin \left({\frac {\pi }{n}}\right)}}\right)$	$\gamma _{2}=\arctan \left({\frac {a}{{\sqrt {2}}\cdot h}}\right)$	$\gamma _{2}=\arctan \left({\frac {a}{{\sqrt {3}}\cdot h}}\right)$
Пространствен ъгъл в ъглите на основата	$\Omega _{1}=4\cdot \arctan \left({\sqrt {\tan \left({\frac {2\cdot \alpha _{1}+\alpha }{4}}\right)\cdot \tan \left({\frac {2\cdot \alpha _{1}-\alpha }{4}}\right)\cdot \tan ^{2}\left({\frac {\alpha }{4}}\right)}}\right)$
Пространствен ъгъл във върха	${\begin{aligned}\Omega _{2}&=4\cdot n\cdot \arctan \left({\sqrt {\tan \left({\frac {2\cdot \gamma _{2}+\alpha _{3}}{4}}\right)\cdot \tan \left({\frac {2\cdot \gamma _{2}-\alpha _{3}}{4}}\right)\cdot \tan ^{2}\left({\frac {\alpha _{3}}{4}}\right)}}\right)\\&=2\cdot \pi -2\cdot n\cdot \arcsin \left(\cos \left({\frac {\pi }{n}}\right)\cdot {\sqrt {\tan ^{2}\left({\frac {\pi }{n}}\right)-\tan ^{2}\left({\frac {\alpha _{3}}{2}}\right)}}\right)\\\end{aligned}}$

Забележки: Питагоровата теорема, теореми за тригонометрични функции и теореми за аркустангенса се използват за извеждане на повечето формули.

Пространствен ъгъл при върховете на основата, където три странични стени (един правилен многоъгълник и два равнобедрени триъгълника) се срещат с вътрешни ъгли α, α₁, α₁, се изчислява с теоремата на Л'Юилие.^[5]

Пространствен ъгъл при върха, където се срещат $n$ странични стени, може да се изчисли и с помощта на теоремата на Л'Юилие чрез разлагане на правилната пирамида на $n$ неправилни тетраедъра с дължини на ръбовете $a,l,l,h,R_{u},R_{u}$ , където $R_{u}={\tfrac {a}{2\cdot \sin \left({\frac {\pi }{n}}\right)}}$ е радиусът на описаната окръжност около правилната основа. Поради ротационната симетрия, телесният ъгъл при върха се разлага на $n$ равни и еднакви частични ъгъла. По този начин тези $n$ неправилни тетраедъра споделят общ връх. В този връх се срещат три стени, всяка с вътрешни ъгли α₃, γ₂ и γ₂.

Друг начин за изчисляване на пространствения ъгъл при върха е да се приложи формулата на Х. С. Раджпут за ротационно симетричния телесен ъгъл при върха.^[6] В този случай вътрешните ъгли на всичките $n$ стени, срещащи се при върха, трябва да са равни, което е вярно за всички правилни пирамиди.

Описани и вписани тела

За пирамидите могат да съществуват вписани и описани геометрични тела при определени условия. Необходимите и достатъчни условия (НДУ) за това са формулирани от теореми.

Сфера

Сферата се нарича описана около пирамидата, ако върховете на пирамидата лежат на повърхността на сферата.

Теорема 1: Около пирамида може да бъде описана сфера, само когато основата на пирамидата е многоъгълник, около който може да се опише окръжност (НДУ). ^[7]
Центърът на сферата ще бъде точката на пресичане на равнините, минаващи през средните точки на ръбовете на пирамидата, перпендикулярни на тях. От тази теорема следва, че една сфера може да бъде описана както за всяка триъгълна, така и за всяка правилна пирамида.

Теорема 2: Сфера може да бъде вписана в пирамида, когато симетралните равнини на вътрешните двустенни ъгли на пирамидата се пресичат в една точка (необходимо и достатъчно условие). Тази точка ще бъде центърът на сферата.

Конус

Конусът се нарича описан около пирамида, когато върховете им съвпадат и основата му е описана около основата на пирамидата.

Теорема 3: Около пирамида може да се опише конус само когато всички странични ръбове на пирамидата са равни (необходимо и достатъчно условие).

Конусът се нарича вписан в пирамида, ако върховете им съвпадат и основата му е вписана в основата на пирамидата.

Теорема 4: В пирамида може да се впише конус само когато апотемите на пирамидата са равни (необходимо и достатъчно условие); ^[8]

Височините на вписани и описани конуси и пирамиди са равни.

Цилиндър

Цилиндърът се нарича описан около пирамидата, ако върхът на пирамидата лежи на една от неговите основи, а другата му основа е описана около основата на пирамидата.

Теорема 5: Около пирамида може да се опише цилиндър само когато около основата на пирамидата има описан многоъгълник (необходимо и достатъчно условие).

Цилиндърът се нарича вписан в пирамида, ако едната му основа съвпада с обиколката на равнина, вписана в сечението на пирамидата, успоредно на основата, а другата основа принадлежи на основата на пирамидата.

Призма

Описаната призма около пирамида може да има с нея обща стена или само общи върхове:

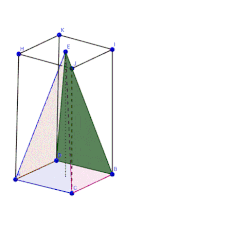
Равностенен неправилен тетраедър с описан правоъгълен паралелепипед

Теорема 6: Ако в

n

-ъгълна пирамида е вписана права

n

-ъгълна призма, на която върховете на горната основа принадлежат към страничните ръбове на пирамидата, тогава съотношението на площта на основата на пирамидата към площта на основата на правата призма с най-големия обем винаги е

{\frac {9}{4}}

.

Общомедия

Общомедия разполага с мултимедийно съдържание за

Пирамида.

Вижте също

Източници

↑ Александров А. Д., Вернер А. Л. –. Геометрия. Учебник для 10—11 классов общеобразовательных учреждений. „Просвещение“. М., 2-е издание, 2003. ISBN 5-09-010773-4. с. 271. (на руски)
↑ Математика в понятиях, определениях и терминах. Ч. 1. Пособие для учителей. Под ред. Л. В. Сабинина. М., „Просвещение“, 1978. 320 с. С. 253 (на руски).
↑ Кушнир И. А. – Триумф школьной геометрии, ISBN 966-8174-01-1, 432 стр., К., издат. „Наш час“, 2005 (на руски).
↑ Hans-Joachim Bartsch: Mathematische Formeln. 5., unveränderter Nachdruck der 11. Auflage, Buch- und Zeit-Verlagsgesellschaft, Köln 1977, S. 152 (на немски).
↑ Wolfram MathWorld – Spherical Excess (на английски)
↑ Solid angles subtended by the platonic solids (regular polyhedra) at their vertices // SlideShare. 3.2015. Посетен на 3.9.2025.
↑ Саакян С. М., Бутузов В. Ф. – Изучение геометрии в 10—11-х классах: книга для учителя, 4-е дораб. изд., 248 стр., ISBN 978-5-09-016554-9, серия „Математика и информатика“, М., изд. „Просвещение“, 2010 (на руски).
↑ Погорелов А. В. – Геометрия: Учебник для 10—11 классов общеобразовательных учреждений, 8-е издание, ISBN 978-5-09-019708-3, 175 стр., тираж 60000, М., „Просвещение“, 2008 (на руски).

[Геометрия-1] Александров А. Д., Вернер А. Л. –. Геометрия. Учебник для 10—11 классов общеобразовательных учреждений. „Просвещение“. М., 2-е издание, 2003. ISBN 5-09-010773-4. с. 271. (на руски)

[2] Математика в понятиях, определениях и терминах. Ч. 1. Пособие для учителей. Под ред. Л. В. Сабинина. М., „Просвещение“, 1978. 320 с. С. 253 (на руски).

[hrono1600-3] Кушнир И. А. – Триумф школьной геометрии, ISBN 966-8174-01-1, 432 стр., К., издат. „Наш час“, 2005 (на руски).

[4] Hans-Joachim Bartsch: Mathematische Formeln. 5., unveränderter Nachdruck der 11. Auflage, Buch- und Zeit-Verlagsgesellschaft, Köln 1977, S. 152 (на немски).

[5] Wolfram MathWorld – Spherical Excess (на английски)

[6] Solid angles subtended by the platonic solids (regular polyhedra) at their vertices // SlideShare. 3.2015. Посетен на 3.9.2025.

[7] Саакян С. М., Бутузов В. Ф. – Изучение геометрии в 10—11-х классах: книга для учителя, 4-е дораб. изд., 248 стр., ISBN 978-5-09-016554-9, серия „Математика и информатика“, М., изд. „Просвещение“, 2010 (на руски).

[8] Погорелов А. В. – Геометрия: Учебник для 10—11 классов общеобразовательных учреждений, 8-е издание, ISBN 978-5-09-019708-3, 175 стр., тираж 60000, М., „Просвещение“, 2008 (на руски).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]