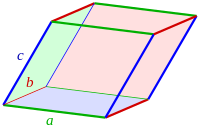
Паралелепипед

Правоъгълен паралелепипед

Паралелепипед (от гръцки: παράλλος – паралелен; επιπεδον – плоскост) е геометрично тяло с шест стени и дванадесет ръба, които са два по два успоредни, и осем върха. Той е частен случай на четиристенна призма с основа успоредник. Най-често се разглежда вариантът, при който всички стени сключват прав ъгъл с неуспоредните на тях – правоъгълен паралелепипед. Правоъгълен паралелепипед, чийто ръбове са еднакво дълги, се нарича куб. Всички стени на произволен паралелепипед са успоредници, на правоъгълен паралелепипед – правоъгълници, а на куб – квадрати.

Първата известна употреба на наименованието е в Евклидовите „Елементи“.

Обем

Обемът на правоъгълен паралелепипед е равен на произведението на дължината, ширината и височината му. При куба те са равни и обемът му е равен на трета степен от дължината на страната. Общия случай може чрез разместване да бъде приведен към правоъгълен паралелепипед и обемът на произволен паралелепипед е равен на произведението на площта на основата по височината му.

$V=S_{ABCD}\cdot h$

Възможно е обемът да бъде изчислен с методите на векторното смятане: ако един от върховете бъде приет за начало на декартова координатна система и трите ръба, излизащи от върха, бъдат представени като вектори ${\vec {a}}=(a_{1},a_{2},a_{3})$, ${\vec {b}}=(b_{1},b_{2},b_{3})$ и ${\vec {c}}=(c_{1},c_{2},c_{3})$, то обемът е равен на абсолютната стойност на смесеното произведение на векторите $({\vec {a}},{\vec {b}},{\vec {c}})$.

$V=|({\vec {a}},{\vec {b}},{\vec {c}})|=\left|{\mathrm {det} }\left({\begin{matrix}a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\c_{1}&c_{2}&c_{3}\end{matrix}}\right)\right|$

• Доказателство:

Понеже $S_{ABCD}=\Vert {\vec {a}}\times {\vec {b}}\Vert$ и $h=\Vert \mathrm {proj} _{{\vec {a}}\times {\vec {b}}}{\vec {c}}\Vert$, то формулата за обем на паралелепипед придобива следният вид: $V=\Vert {\vec {a}}\times {\vec {b}}\Vert \cdot \Vert \mathrm {proj} _{{\vec {a}}\times {\vec {b}}}{\vec {c}}\Vert =\Vert {\vec {a}}\times {\vec {b}}\Vert \cdot {\dfrac {|({\vec {a}},{\vec {b}},{\vec {c}})|}{\Vert {\vec {a}}\times {\vec {b}}\Vert }}=|({\vec {a}},{\vec {b}},{\vec {c}})|$

Свойства

Някои геометрични свойства на паралелепипеда са:

• паралелепипедът е централно-симетричен спрямо средата на телесния му диагонал (следствие от централната симетрия на стените му);
  • всяка отсечка с краища върху паралелепипед и минаваща през средата на телесния му диагонал се разполовява от тази среда;
  • в частност всички телесни диагонали се пресичат и разполовяват в една точка;
• успоредните помежду си ръбове на паралелепипеда са равни по дължина;
• успоредните стени са еднакви успоредници и съответно имат еднакви обиколка и площ;
• квадрата на дължината на телесния диагонал на правоъгълен паралелепипед е равен на сумата на квадратите на трите му размерности (следствие от Питагоровата теорема).